1. 파형이란 무엇인가?
전자 공학에서 ‘파형’은 시간에 따라 변화하는 신호의 모양을 나타냅니다.
마치 하늘에 그려진 구름 모양이 다양한 것처럼, 신호의 모양도 각기 다르게 나타납니다.
이 신호의 모양을 이해하는 것은 매우 중요합니다.
왜냐하면, 신호가 어떻게 변하는지를 알아야 그 신호가 실제로 어떤 정보를 담고 있는지 또는 어떤 현상을 나타내고 있는지를 알 수 있기 때문입니다.
1-1) 파형의 기본 개념
파형의 기본적인 개념은 신호가 시간에 따라 어떻게 변하는지를 보여주는 그래프입니다.
우리가 일상에서 듣는 소리, 보는 영상, 심지어 몸의 심장 박동까지도 모두 ‘파형’으로 표현될 수 있습니다.
예를 들어, 라디오에서 나오는 소리는 사실 특정한 주파수 대역을 가지는 전자기 신호인데, 이 신호의 모양을 파형으로 나타낼 수 있습니다.
기본 파형의 종류로는 사인파, 삼각파, 사각파 등 다양한 종류가 있습니다.
각각의 파형은 특유의 모양을 가지고 있으며, 이 모양에 따라 그 신호가 어떻게 동작할지 결정됩니다.
1-2) 주기, 진폭, 주파수 설명
파형을 이해하기 위해선 세 가지 중요한 개념을 알아야 합니다.
주기, 진폭, 그리고 주파수입니다.
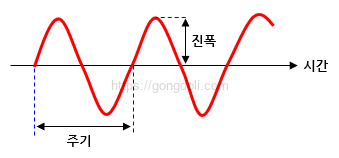
- 주기(Period): 주기는 파형이 한 번 완전히 반복되는 데 걸리는 시간을 의미합니다.
예를 들어, 시계의 초침이 한 바퀴 도는 시간이 60초라면, 이 60초가 주기입니다.
전자파형에서도 마찬가지로 한 주기가 완료되는 시간은 중요한 요소입니다. - 진폭(Amplitude): 진폭은 파형의 ‘높이’를 말합니다.
파형의 가장 높은 지점과 가장 낮은 지점 사이의 차이가 바로 진폭입니다.
진폭이 클수록 그 신호는 더 강한 에너지를 가지게 됩니다.
예를 들어, “스피커에서 소리가 너무 작아요”라는 질문이 있었는데, 이는 진폭이 낮기 때문일 수 있습니다.
이럴 경우, 진폭을 높이면 더 큰 소리가 나게 되는 거죠. - 주파수(Frequency): 주파수는 파형이 1초에 몇 번 반복되는지를 나타내는 값입니다.
흔히 헤르츠(Hz) 단위로 표현합니다.
주파수가 높을수록 더 빠르게 진동하는 신호를 뜻합니다.
주파수는 우리 일상생활에서도 자주 들어본 개념일 겁니다.
예를 들어, 라디오에서 98.1MHz 주파수를 맞추는 것처럼요.
파형의 기본 파형의 종류는 주기, 진폭, 주파수에 따라 그 모양과 특징이 달라집니다.
예를 들어, 사인파는 부드럽고 연속적인 곡선 모양을 가지며, 삼각파는 직선으로 위아래로 반복되고, 사각파는 급격한 상승과 하강을 반복합니다.
각각의 파형은 신호를 전달하거나 전기적 특성을 설명하는 데 매우 중요한 역할을 합니다.
- 연관 참조 : 비안정 멀티바이브레이터 회로, 동작 원리, 예제2, 주파수 표, 구동 회로
- 연관 참조 : 단안정 멀티바이브레이터 회로, 동작 원리, 트랜지스터 기반 회로, TTL/CMOS 기반 회로
- 연관 참조 : 쌍안정 멀티바이브레이터 회로, 동작 원리, 유형, 비교 및 장.단점
- 연관 참조 : NE555 회로 설계,핀 구성, 5핀 사용 이유, 동작 모드별 설명,
2. 사인파 (Sine Wave)
기본 파형의 종류 중에 사인파는 전자공학과 신호 처리에서 가장 기본이 되는 파형입니다.
사실, 우리가 자연에서 관찰할 수 있는 많은 물리적 현상들이 사인파의 형태를 따릅니다.
예를 들어, 소리나 빛의 파동도 기본적으로 사인파 형태로 설명할 수 있습니다.
그래서 사인파는 기본 파형의 종류 중에서도 가장 중요한 파형이라고 할 수 있습니다.
2-1) 정의와 특징
사인파는 시간에 따라 부드럽게 올라갔다가 내려오는 파형입니다.
수학적으로는 sin(x) 함수로 표현할 수 있으며, 특정 주기마다 반복되는 것이 특징입니다.
이때 사인파는 대칭적이고, 중간점을 기준으로 파형이 위로도 아래로도 같은 진폭을 가지고 움직입니다.
특히, 사인파는 기본 파형의 종류 중에서 가장 ‘순수한’ 형태의 파형이라고 불립니다.
이는 사인파가 고조파(다른 주파수의 성분)가 전혀 없이 오직 한 가지 주파수만을 포함하고 있기 때문입니다.
그래서 사인파는 매우 간결하고 깔끔한 모양을 가지고 있습니다.
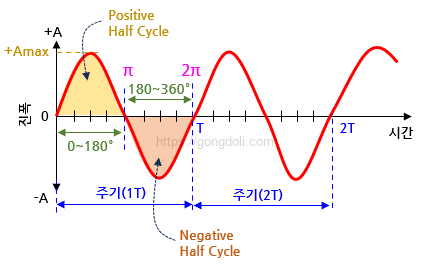
주기(Periodic Time)의 단위는 보통 초(s), 밀리초(ms), 그리고 마이크로초(μs)로 표현됩니다.
특히 사인파 파형의 경우, 주기를 각도(도) 또는 라디안으로도 표현할 수 있습니다.
한 사이클이 360도( T = 360º ) 또는 라디안으로는 2π ( T = 2π )에 해당합니다.
따라서 2π 라디안은 360도와 같다는 사실을 꼭 기억해야 합니다!
우리는 전기 파형이 자신을 반복하는 데 걸리는 시간을 주기 또는 기간이라고 부르며, 이는 일정한 시간 간격을 나타냅니다.
이 주기(T)의 역수(1/T)를 계산하면, 해당 파형이 1초에 몇 번 반복되는지를 나타내는 값이 나옵니다.
이것이 바로 주파수(Hz)입니다.
주파수는 초당 사이클(Cycles per Second, cps)로도 표현되며, 1Hz는 정확히 1초에 1번의 사이클을 뜻합니다.
주기와 주파수는 서로 역수 관계를 가지며, 파형의 주기가 짧아질수록 주파수는 커집니다.
반대로 주기가 길어지면 주파수는 감소합니다.
주기와 주파수의 관계는 다음과 같습니다.
f = 1/T(Hz)
T = 1/f(sec)
여기서, ƒ는 주파수(Hz)이고, T는 주기(초)입니다.
1Hz는 초당 1사이클과 정확히 같지만, 1Hz는 매우 작은 단위이기 때문에, kHz(킬로헤르츠), MHz(메가헤르츠), 그리고 GHz(기가헤르츠)와 같은 접두사를 사용하여 파형의 크기를 나타냅니다.
2-2) 사인파가 중요한 이유
사인파가 중요한 이유는 그 단순함과 정확성에 있습니다.
많은 신호 처리나 통신 시스템에서는 다양한 복잡한 파형들을 사인파의 조합으로 분해하여 분석합니다.
“신호 처리가 무엇인가요?”라는 질문을 찾아보면, 신호 처리의 기본 개념에서 바로 사인파가 등장하는 것을 볼 수 있습니다.
왜냐하면 사인파는 모든 복잡한 파형을 만들기 위한 기본 단위로 사용될 수 있기 때문입니다.
또한, 사인파는 통신에서 매우 중요한 역할을 합니다.
전파가 공중을 통해 전달될 때, 대부분의 전파는 사인파의 형태로 변조됩니다.
이는 사인파가 왜곡 없이, 그리고 불필요한 신호 성분을 최소화하며 신호를 전달할 수 있기 때문입니다.
그리고 무엇보다 사인파는 주기성과 안정성 덕분에 매우 정확한 타이밍을 요구하는 시스템에서 유용하게 사용됩니다.
예를 들어, 전자 시계나 GPS 시스템에서 사인파는 정확한 시간 계산을 위해 필수적입니다.
2-3) 사인파의 실제 응용 사례 (통신, 음악 등)
사인파의 실제 응용 사례는 우리 생활 곳곳에서 찾아볼 수 있습니다.
그중에서도 가장 대표적인 분야가 바로 통신과 음악입니다.
- 통신에서의 사인파: 통신 시스템에서는 사인파가 정보 전달을 위한 매개체로 자주 사용됩니다.
예를 들어, 라디오나 텔레비전 방송에서는 정보를 전파에 실어 보내기 위해 사인파를 변조합니다.
이 과정에서 사인파의 주파수나 진폭을 조절하여 음성, 영상 등 다양한 정보를 전달할 수 있게 되는 것입니다.
흔히 “라디오 주파수를 맞추는 이유는?”이라는 질문을 볼 수 있는데, 여기서 바로 이 사인파를 맞추는 과정을 설명할 수 있습니다. - 음악에서의 사인파: 음악에서는 악기의 소리가 기본적으로 파형으로 나타납니다.
특히, 순수한 톤을 생성하는 신디사이저 등에서는 사인파를 사용하여 부드러운 소리를 만듭니다.
고전적인 전자 악기나 사운드 디자인에서도 사인파는 중요한 기본 파형의 종류로 활용됩니다.
이를 통해, 부드럽고 명확한 소리를 만들어 낼 수 있으며, 다른 파형들과 조합하여 다양한 소리를 낼 수 있습니다. - 의료와 과학에서의 사인파: 심장 박동기나 뇌파 측정 장비에서도 사인파는 중요한 역할을 합니다.
심전도(ECG)나 뇌전도(EEG)에서 나오는 신호는 사인파를 기반으로 분석됩니다.
이처럼 사인파는 의료기기에서 생체 신호를 분석하고 측정하는 데 매우 유용합니다.
3. 삼각파 (Triangle Wave)
삼각파 또한 기본 파형의 종류 중 하나로, 그 이름처럼 파형의 모양이 마치 삼각형처럼 생긴 것이 특징입니다.
부드러운 곡선 형태의 사인파와는 달리, 삼각파는 직선으로 이루어진 일정한 기울기를 가진 상승과 하강을 반복합니다.
3-1) 정의와 특징
삼각파는 특정 주기 동안 직선적으로 상승했다가, 다시 직선적으로 하강하는 파형입니다.
말 그대로, 산의 꼭대기에서 내려오는 듯한 모양을 가집니다.
한 주기 내에서 상승과 하강이 균일한 기울기를 가지고 있기 때문에, 그 파형은 매우 대칭적입니다.
삼각파는 일반적으로 양의 피크와 음의 피크 사이를 오가는 비정현(non-sinusoidal) 파형으로, 양방향으로 진동합니다.
비록 삼각형 모양을 하고 있지만, 삼각파는 실제로 대칭적인 선형 램프(linear ramp) 파형에 가깝습니다.
이는 일정한 주파수나 속도로 천천히 상승하고 하강하는 전압 신호이기 때문입니다.
삼각파의 상승과 하강 속도는 주기 내에서 동일하며, 이는 기본 파형의 종류 중에서 독특한 특성입니다.
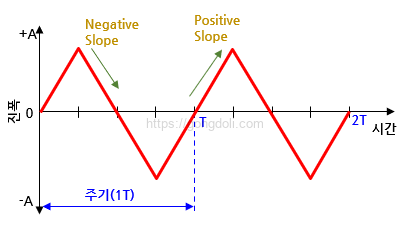
삼각파는 대개 상승 구간(positive-going ramp)과 하강 구간(negative-going ramp)이 동일한 시간을 가지며, 이로 인해 삼각파는 50% 듀티 사이클을 가집니다.
즉, 삼각파는 한 주기 내에서 상승과 하강이 균일하게 이루어집니다.
이 때문에 기본 파형의 종류 중에서 매우 대칭적인 파형으로, 일정한 주파수를 유지합니다.
삼각파의 평균 전압은 파형의 주파수에 따라 달라집니다.
예를 들어, 상승과 하강 시간이 느릴수록 평균 전압은 낮아지며, 반대로 빠른 상승과 하강을 가질 경우 평균 전압이 높아집니다.
특히 삼각파는 기본 파형의 종류 중에서 고조파 성분이 많다는 점이 특징입니다.
고조파란 기본 주파수 외에 파형 속에 포함된 여러 배수 주파수들인데, 삼각파는 사각파보다 고조파 성분이 상대적으로 적지만 여전히 포함되어 있어 파형이 날카로운 소리를 냅니다.
3-2) 삼각파의 생성 방식
삼각파는 주로 오실레이터(oscillator)라는 회로를 통해 생성됩니다.
오실레이터는 일정한 주파수로 신호를 발생시키는 장치로, 삼각파를 만들 때는 특히 적분기(integrator) 회로를 많이 사용합니다.
적분기는 사각파 신호를 받아서 삼각파로 변환하는 역할을 합니다.
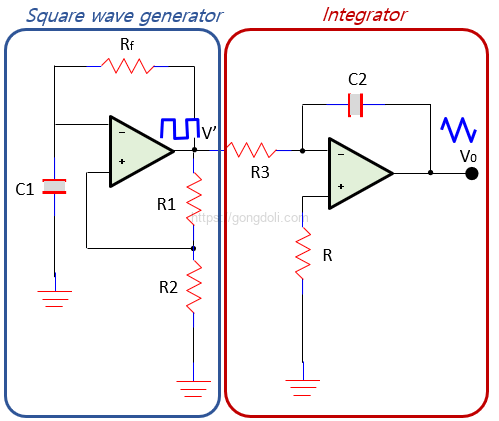
쉽게 말하면, 사각파는 급격히 상승과 하강을 반복하는 신호인데, 이를 적분기로 처리하면 각 변화를 부드럽게 직선으로 연결해 삼각파가 되는 것입니다.
이때 발생하는 삼각파의 기울기는 사각파의 주파수와 연관이 있습니다.
3-3) 비대칭 삼각파와 톱니파
삼각파의 대칭성을 깨트려 비대칭적인 삼각파를 만들 수도 있습니다.
이를 위해 상승 구간과 하강 구간의 속도를 다르게 설정하면 됩니다.
이러한 방식으로 생성된 파형을 톱니파(sawtooth waveform)고 부르며, 이는 기본 파형의 종류 중에서 또 다른 독특한 형태를 제공합니다.
톱니파는 삼각파와 달리 상승 또는 하강 중 하나가 더 빠르거나 느리게 진행되는 파형입니다.
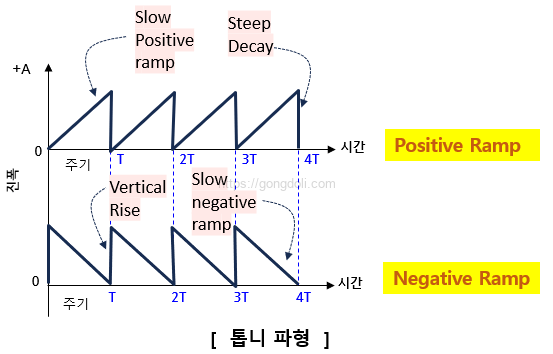
톱니파는 기본 파형의 종류 중에서도 매우 독특한 파형으로, 주로 양의 램프 구간이 특징적인 양방향 톱니파(positive ramp sawtooth waveform)가 가장 많이 사용됩니다.
이 톱니파는 상승 구간이 거의 완벽하게 선형적인 형태를 띄며, 함수 발생기(function generator)에서 흔히 생성할 수 있는 파형입니다.
톱니파는 기본 주파수(ƒ)와 모든 고조파 성분이 포함된 파형으로, 고조파의 비율은 1/2, 1/4, 1/6, 1/8… 1/n 등의 정수 배로 나타납니다.
실질적으로 이는 톱니파가 매우 풍부한 고조파를 포함하고 있다는 의미입니다.
이러한 특성 덕분에 기본 파형의 종류 중에서 톱니파는 음향적으로 매우 중요한 역할을 합니다.
특히 음악 신디사이저와 같은 전자악기에서 톱니파는 소리의 음색과 질감을 풍부하게 만들어 줍니다.
고조파가 많기 때문에 왜곡 없이도 소리의 질감을 다양하게 표현할 수 있어, 음악가들이 흔히 사용하는 파형 중 하나입니다.
톱니파는 복잡한 고조파를 통해 독특한 음향적 색채를 제공하여 음악에서 중요한 역할을 합니다.
3-4) 삼각파의 응용 분야 (계측기, 전자악기 등)
삼각파는 기본 파형의 종류 중에서 매우 다양한 응용 분야를 가지고 있습니다.
그중에서도 대표적인 두 가지는 계측기와 전자악기 분야입니다.
- 계측기: 삼각파는 주로 신호를 분석하거나 테스트하는 데 사용됩니다.
예를 들어, 오실로스코프 같은 측정 장비는 다양한 파형을 분석하는 데 삼각파를 자주 사용합니다.
그 이유는 삼각파의 대칭성과 직선적 특성 덕분에, 신호의 정확성을 쉽게 평가할 수 있기 때문입니다.
삼각파는 정밀한 시간 측정을 필요로 하는 시스템에서 기본 테스트 신호로도 사용됩니다. - 전자악기: 전자 음악에서 삼각파는 매우 중요한 기본 파형의 하나입니다.
삼각파는 사각파보다 부드럽지만, 여전히 날카로운 소리를 냅니다.
이 때문에 전자악기에서 다양한 음색을 만들 때 삼각파가 자주 사용됩니다.
예를 들어, “신디사이저에서 삼각파는 어떤 소리를 낼까요?”
삼각파는 특히 고음역대의 밝고 날카로운 소리를 내는 데 적합합니다.
이처럼 삼각파는 독특한 음색을 통해 전자음악의 중요한 요소로 자리 잡고 있습니다.
4. 사각파 (Square Wave)
사각파는 기본 파형의 종류 중에서도 매우 단순하지만 강력한 파형으로, 일정한 주기 동안 전압이 급격하게 최댓값과 최솟값 사이를 오가는 형태를 가지고 있습니다.
이 때문에 파형이 ‘사각형’처럼 보이며, 전자 회로나 디지털 신호 처리에서 중요한 역할을 합니다.
사각파는 대부분 디지털 신호와 직접적으로 연결되어 있어, 실생활에서도 쉽게 접할 수 있는 기본 파형의 종류 중 하나입니다.
4-1) 정의와 특징
사각파는 주기적으로 최댓값과 최솟값을 빠르게 전환하는 파형입니다.
가장 큰 특징은, 상승과 하강 구간이 매우 급격하게 이루어진다는 점입니다.
즉, 주기 동안 전압이 거의 순간적으로 변하며, 한 주기 동안 높은 전압 상태와 낮은 전압 상태가 각각 50%의 시간을 차지합니다.
이런 특성 덕분에 사각파는 50% 듀티 사이클을 가지는 대칭 파형으로, 매우 직관적인 파형 중 하나입니다.
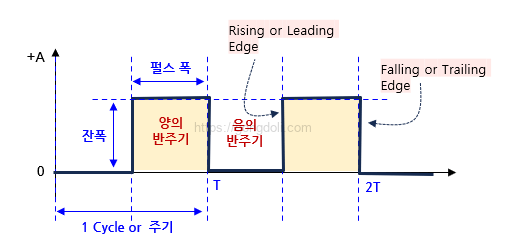
사각형 모양의 전기 파형은 주기 동안 각각의 절반 구간이 동일한 대칭적인 형태를 띠고 있습니다.
즉, 사각파에서 양의 펄스가 나타나는 시간과 음의 펄스 또는 0이 되는 시간이 동일합니다.
특히 디지털 회로에서 사각파가 클럭 신호로 사용될 때, 양의 펄스 구간을 듀티 사이클(Duty Cycle)이라고 부릅니다.
사각파는 기본 파형의 종류 중 하나로, 양의 신호(ON) 구간과 음의 신호(OFF) 구간이 각각 주기의 절반을 차지합니다.
이로 인해 듀티 사이클은 항상 50%를 가지며, 주기 동안 절반의 시간은 신호가 켜져 있고, 나머지 절반의 시간은 신호가 꺼져 있습니다.
또한 주파수(f)는 주기의 역수로 정의되며, 이를 이용해 사각파의 주파수를 계산할 수 있습니다.
기본 파형의 종류 중에서 사각파는 디지털 회로의 클럭 신호나 데이터 타이밍을 정확하게 조정하는 데 매우 중요한 역할을 합니다.
사각파는 디지털 신호와 매우 밀접한 관계가 있습니다.
디지털 신호는 0과 1로 구성된 이진 신호(binary signal)로, 이때 1은 전압이 높은 상태, 0은 전압이 낮은 상태를 의미합니다.
사각파는 이러한 이진 신호를 구현하기에 적합한 파형으로, 컴퓨터와 같은 디지털 장치에서 정보를 처리하는 데 핵심적인 역할을 합니다.
4-2) 사각파의 실생활 응용 (디지털 회로, 클럭 신호 등)
사각파는 다양한 실생활 응용에서 중요한 역할을 합니다.
그 중에서도 대표적인 분야는 디지털 회로와 클럭 신호입니다.
- 디지털 회로: 사각파는 디지털 회로에서 데이터 처리를 위한 기본적인 신호로 사용됩니다.
예를 들어, 마이크로컨트롤러나 CPU는 사각파 형태의 클럭 신호를 통해 명령을 수행하는 속도를 조절합니다.
클럭 신호는 주기적으로 발생하는 사각파로, 각 주기마다 데이터가 처리되거나 명령이 실행됩니다.
사각파의 주파수에 따라 디지털 장치의 작동 속도가 결정됩니다. - 클럭 신호: 클럭 신호는 디지털 장치의 타이밍을 조절하는 신호로, 마치 심장 박동과도 같습니다.
사각파는 빠른 전환을 통해 디지털 시스템에서 정확한 시간 제어를 가능하게 합니다.
예를 들어, 컴퓨터에서 CPU가 명령을 처리하는 데 클럭 신호가 필수적인 역할을 하며, 이 클럭 신호가 바로 사각파 형태로 전달됩니다.
4-3) 예제 풀어보기
예제 1 : 구형파 전기 파형의 펄스 폭은 5ms이며 주파수(ƒ)를 계산해 보겠습니다.
사각파의 펄스 폭이 5ms일 때, 주파수(ƒ)를 계산할 수 있습니다.
주파수는 주기의 역수이므로, 먼저 주기를 계산해야 합니다.
- 펄스 폭이 5ms라면, 이는 ON 상태일 때의 시간입니다.
사각파의 경우 듀티 사이클이 50%이므로, 전체 주기(T)는 이 값의 두 배가 됩니다.
T = 5ms × 2 = 10ms (0.01초) - 주파수는 주기의 역수이므로, 다음과 같이 계산합니다.
ƒ = 1 / T = 1 / 0.01 = 100Hz
따라서 이 사각파의 주파수는 100Hz입니다.
이 값은 사각파가 기본 파형의 종류 중에서 디지털 회로나 클럭 신호로 자주 사용되며, 일정한 주파수를 유지하는 특성 덕분에 여러 전자 장치에서 안정적인 동작을 보장할 수 있다는 점에서도 중요한 의미를 가집니다.
예제 2 : 사각파에서 양의 펄스 폭이 5ms이고, 듀티 사이클이 25%일 때 주파수(ƒ)를 계산해 보겠습니다.
듀티 사이클은 전체 주기에서 양의 펄스가 차지하는 비율로, 다음과 같이 계산됩니다.
f= 1 / T = 1/(5ms + 15ms) = 50Hz
따라서, 이 직사각형 파형의 주파수는 50Hz입니다.
5. 각 파형의 비교
고조파는 기본 주파수의 정수배로 발생하는 파형의 성분입니다.
각 파형은 고조파가 포함된 방식에 따라 그 특성과 소리가 달라집니다.
고조파는 전기 신호뿐만 아니라 소리의 톤과 질감에 큰 영향을 미칩니다.
각 파형이 소리와 신호 처리에 미치는 차이는 매우 큽니다.
- 사인파: 가장 부드럽고 순수한 소리를 전달하며, 고조파가 없기 때문에 왜곡이 없습니다.
오디오 시스템이나 통신에서 선호됩니다. - 삼각파: 고조파가 약하게 포함되어 있어 사인파보다는 약간 거친 소리를 냅니다.
전자 악기에서 사용됩니다. - 사각파: 강한 고조파로 인해 매우 날카롭고 강한 소리를 내며, 디지털 신호 처리에서 필수적인 파형입니다.
- 톱니파: 모든 고조파를 포함해 매우 복잡한 소리를 내며, 전자 음악에서 복잡하고 독특한 소리를 만드는데 사용됩니다.