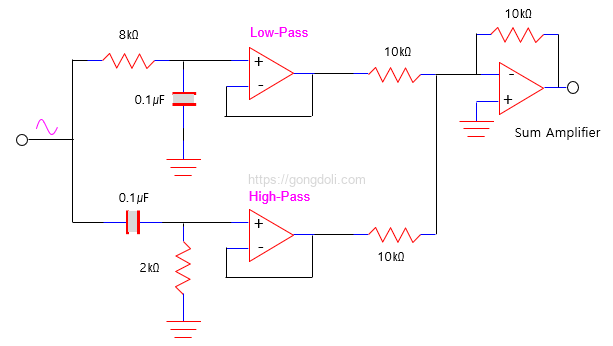
1. 노치 필터 회로란?
Band Stop Filter (BSF), Band Reject Filter (BRF), 또는 노치 필터 회로(Notch Filter)는 특정 주파수 대역의 신호를 차단하고, 그 외의 주파수는 통과시키는 필터입니다.
이 필터는 주로 원하지 않는 특정 주파수 대역의 잡음을 제거하거나, 특정 주파수 대역의 신호를 억제하는 데 사용됩니다.
Band Pass Filter(BPF, 대역 통과 필터)와 노치 필터(Notch Filter)는 반대되는 기능을 수행하는 필터입니다.
BPF는 특정 주파수 대역을 통과시키는 데 사용되며, 노치 필터는 특정 주파수 대역을 차단하는 데 사용됩니다.
Band Stop Filter, Band Reject Filter, 그리고 노치 필터 회로는 모두 특정 주파수 대역을 차단하는 기능을 가지며, 용도와 차단 대역폭의 넓이에 따라 용어가 다르게 사용될 뿐, 기본적인 동작 원리는 동일합니다.
BSF/BRF는 넓은 주파수 대역을 차단하는 반면, 노치 필터 회로는 매우 좁은 특정 주파수 대역을 차단하는 데 특화되어 있습니다.
- 연관 참조 : 버터워스 필터, 주파수 응답, 근사화, 1차 LPF , 이상적인 주파수, 다항식
- 연관 참조 : 능동 대역 통과 필터,동작 원리,회로, 반전 BPF, 예제1
- 연관 참조 : 능동 고역 통과 필터,이상적인 HPF, 전압 이득, 주파수 응답
- 연관 참조 : 능동 저역 통과 필터,1차 LPF, 전압 이득, 예제1
2. 노치 필터 회로 구성 및 동작, 연결 방식
위에서도 설명했듯이 노치 필터 회로 또는 Band Reject Filter(BRF,BSF)는 특정 주파수 대역을 차단하고, 그 외의 주파수는 통과시키는 필터입니다.
이 필터의 동작 원리는 RC 저역 통과 필터(RC Low-Pass Filter)와 RC 고역 통과 필터(RC High-Pass Filter)를 결합하여 중간 주파수 대역을 차단하는 방식에 기반합니다.
2-1) 노치 필터 회로 기본 구성 요소
2-1-1) 저역 통과 필터(Low-Pass Filter, LPF)
- 구성: 저항(R)과 커패시터(C)가 직렬로 연결된 회로입니다.
- 동작 원리: 저주파수 성분은 커패시터를 통해 쉽게 통과하지만, 고주파수 성분은 커패시터에 의해 차단됩니다.
차단 주파수 ƒL = 1 / 2πRC
2-1-2) 고역 통과 필터(High-Pass Filter, HPF)
- 구성: 커패시터(C)와 저항(R)이 직렬로 연결된 회로입니다.
- 동작 원리: 고주파수 성분은 커패시터를 통해 쉽게 통과하지만, 저주파수 성분은 저항에 의해 차단됩니다.
차단 주파수 ƒH = 1 / 2πRC
2-1-3) 결합해서 노치 필터(BSF,BRF) 회로 만들기
노치 필터 회로는 LPF와 HPF를 결합하여 특정 중간 주파수 대역을 차단합니다.
이때 각 필터의 차단 주파수를 조정하여 원하는 주파수 대역을 차단할 수 있습니다.
- 결합 방식: 저역 통과 필터와 고역 통과 필터를 직렬 또는 병렬로 연결하여 사용합니다.
2-2) 동작 원리
-. 직렬 연결
저역 통과 필터(LPF)를 통해 특정 저주파수 이하의 신호를 통과시킵니다.
이후 고역 통과 필터(HPF)를 통해 특정 고주파수 이상의 신호를 통과시킵니다.
결과적으로, 중간 주파수 대역(f_L과 f_H 사이의 주파수)은 두 필터에 의해 차단됩니다.
-. 병렬 연결
저역 통과 필터(LPF)와 고역 통과 필터(HPF)를 병렬로 연결합니다.
입력 신호는 두 필터를 거쳐 병렬로 처리되며, 저역과 고역 주파수는 각각 통과하지만, 중간 주파수 대역은 차단됩니다.
2-3) 연결 방식
2-2-1) 직렬 연결
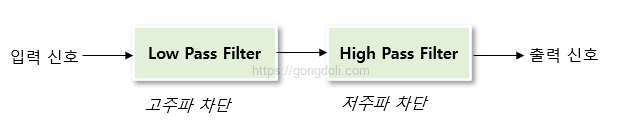
저역 통과 필터가 먼저 저주파수를 통과시키고 고주파수를 차단합니다.
이어서 고역 통과 필터가 고주파수를 통과시키고 저주파수를 차단합니다.
결과적으로 중간 주파수 대역이 차단됩니다.
2-2-2) 병렬 연결
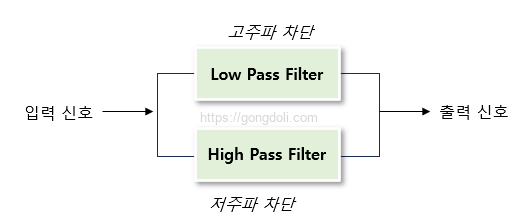
입력 신호가 병렬로 LPF와 HPF를 통과합니다.
LPF가 저주파수를 통과시키고 고주파수를 차단합니다.
HPF가 고주파수를 통과시키고 저주파수를 차단합니다.
두 필터가 병렬로 동작하여 중간 주파수 대역을 차단합니다.
3. 노치 필터 회로 주파수 응답 및 특성
이상적인 Band Stop Filter의 주파수 응답은 차단 대역에서 완벽한 감쇠를 보여야 합니다.
그러나 실제 회로에서는 커패시터의 스위칭 메커니즘과 같은 비이상적인 요소들로 인해 주파수 응답이 이상적인 필터와는 다를 수 있습니다.
3-1) 이상적인 주파수 응답

이상적인 Band Stop Filter는 차단 대역에서 완벽한 감쇠(무한 감쇠)를 보여야 합니다.
두 컷오프 주파수 사이의 대역(fL에서 fH까지)이 완전히 차단됩니다.
3-2) 실제적인 주파수 응답
실제 회로에서는 커패시터와 같은 부품의 비이상적인 특성으로 인해 주파수 응답이 이상적이지 않을 수 있습니다.
차단 대역에서 완벽한 감쇠를 보여주지 않으며, 약간의 신호가 통과할 수 있습니다.
통과 대역에서의 이득(gain)은 저역 통과 필터와 고역 통과 필터의 이득과 동일해야 합니다.
아래 그림은 Band Stop Filter의 이상적 및 실제 주파수 응답을 나타냅니다. 초록색 선은 실제 주파수 응답을 나타냅니다.
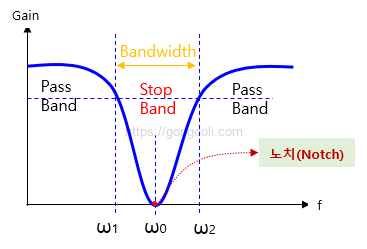
노치 필터 회로(또는, Band Stop Filter)는 저역 통과 필터와 고역 통과 필터를 결합하여 특정 주파수 대역을 차단하는 필터입니다.
이상적인 주파수 응답은 차단 대역에서 완벽한 감쇠를 보여야 하지만, 실제 회로에서는 비이상적인 요소로 인해 이상적인 응답과 차이가 있을 수 있습니다.
이러한 실제 응답은 통과 대역에서 저역 통과 필터와 고역 통과 필터의 이득과 동일해야 하며, 차단 대역에서의 감쇠가 이상적이지 않을 수 있습니다.
3-3) 특성
노치 필터(Notch Filter)는 매우 좁은 대역의 특정 주파수를 강하게 차단하고, 나머지 주파수는 거의 영향을 받지 않고 통과시키는 필터입니다.
주로 잡음 제거나 특정 주파수 성분의 억제에 사용되며, 중심 주파수에서의 감쇠 깊이가 깊고, 주파수 응답 곡선이 매우 가파른 특징을 가집니다.
이러한 특성 덕분에 노치 필터는 전자기기나 오디오 장비 등에서 불필요한 신호를 제거하는 데 효과적으로 사용됩니다.
4. 노치 필터 회로 설계
Band Stop Filter 회로 설계에서 연산 증폭기(Operational Amplifier)를 사용하면 기본 필터 회로에 전압 이득을 추가할 수 있습니다.
두 비반전 전압 팔로워(non-inverting voltage follower)는 입력 및 피드백 저항을 추가하여 기본 비반전 증폭기로 쉽게 변환할 수 있으며,
그 이득은 Av=1+Rf / Rin 입니다.
또한, -3dB 컷오프 주파수가 1kHz와 10kHz이고, 중간 차단 대역에서 -10dB의 이득을 갖는 Band Stop Filter가 필요하다면, 이러한 요구 사항을 충족하는 저역 통과 필터(LPF)와 고역 통과 필터(HPF)를 설계하여 이를 직렬로 연결하면 넓은 대역의 Band Pass Filter를 형성할 수 있습니다.

이제 노치 필터 회로(Band Stop Filter)의 원리를 이해했으니, 이전의 컷오프 주파수 값을 사용하여 하나를 설계해 보겠습니다.
4-1) 노치 필터 회로 설계(예시)
노치 필터 회로(Band Stop Filter)의 동작 원리와 예시 회로 설계를 설명하겠습니다.
200Hz의 낮은 차단 주파수와 800Hz의 높은 차단 주파수를 가지는 기본적인 광대역 RC 대역 정지 필터를 설계해 보겠습니다.
회로의 중심 주파수, -3dB 대역폭과 Q를 구해보겠습니다.
4-1-1) 설계 목표
- 낮은 컷오프 주파수 (𝑓𝐿fL): 200Hz
- 높은 컷오프 주파수 (𝑓𝐻fH): 800Hz
-. 중심 주파수는?
중심 주파수 (𝑓0)는 두 컷오프 주파수의 평균으로 계산됩니다.
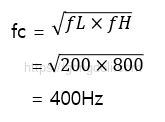
-. -3dB 대역폭?
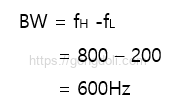
-. Q 값?

4-1-2) 회로 구성
-. 컷오프 주파수 계산
각 필터 섹션의 컷오프 주파수는 저역 통과 필터와 고역 통과 필터의 공식을 사용하여 계산할 수 있습니다.
커패시터C 값이 0.1µF인 경우, 주파수 결정 저항𝑅𝐿과 𝑅𝐻값을 다음과 같이 계산합니다.
-. 저역 통과 필터 섹션
저역 통과 필터의 컷오프 주파수 공식은
𝑓𝐿=1/2𝜋𝑅𝐿𝐶
여기서 𝑓𝐿=200Hz, C=0.1µF이므로 RL 값을 구하면
200=1/(2𝜋𝑅𝐿×0.1×10−6 )
𝑅𝐿=1/(2𝜋×200×0.1×10−6)
𝑅𝐿≈7.96 kΩ
-. 고역 통과 필터 섹션
𝑓H=1/2𝜋𝑅H𝐶
여기서 𝑓H=800Hz, C=0.1µF이므로 RH 값을 구하면
800=1/(2𝜋𝑅H×0.1×10−6 )
𝑅𝐿=1/(2𝜋×800×0.1×10−6)
𝑅𝐿≈1.99 kΩ
4-1-3) 최종 회로 설계
이제 두 필터 섹션의 구성 요소 값을 알았으므로, 이를 단일 전압 가산 회로로 결합할 수 있습니다.
연산 증폭기의 피드백 저항과 두 입력 저항이 모두 10kΩ이라면, 반전 합산 회로는 두 입력 신호의 수학적으로 정확한 합을 제공하며, 전압 이득은 0입니다.