Contents
1. 개요
Norton의 정리는 Thevenin의 정리와는 달리 회로의 일부를 전류원과 병렬 저항으로 이루어진 등가 회로로 대체합니다.
이 정리는 1926년에 E.L. Norton에 의해 제안된 Thevenin의 정리의 확장 개념입니다.
Thevenin의 정리와 유사하게, Norton의 정리도 간단한 계산을 통해 부하 전압, 부하 전류 및 부하 전력과 같은 부하 변수를 계산하는 데 사용됩니다.
따라서 이 정리는 Thevenin의 정리의 이중성이라고도 불립니다.
대부분의 경우, 최대 전력을 부하에 전달하기 위한 부하 저항의 선택은 Thevenin의 정리 또는 Norton의 정리 중 하나에 의해 결정됩니다.
노턴의 등가 회로는 노턴의 정리에 기반하여 구성됩니다.
노턴의 정리는 원래 회로를 단순화하여 등가 전류원과 등가 저항으로 구성된 회로로 대체하는 것을 의미합니다.
이를 통해 복잡한 회로를 단순화하고 분석을 용이하게 할 수 있습니다.
Norton의 정리는 Thevenin의 정리와 밀접하게 연관되어 있으며, 회로 분석에서 매우 유용합니다.
이러한 이유로, 전기 공학 및 회로 이론에서 Norton의 정리는 핵심 개념 중 하나로 자리 잡고 있습니다.
- 연관 참조 : 키르히호프의 회로 법칙, KCL, KVL, 예제, KCL vs. KVL,적용과 한계
- 연관 참조 : 메쉬 전류 분석,Mesh Current Analysis,예제, 장점 3가지, 다른 분석과 비교
- 연관 참조 : 노드 전압 분석, 분석 방법 5단계, 예제, 메쉬 전류 분석과 비교
- 연관 참조 : 테브난의 정리, 5단계 방법, 예제, 한계와 주의 사항
- 연관 참조 : 밀만의 정리, 등가 회로, 예제,옴의 법칙과 키르히호프 법칙과 비교,한계
- 연관 참조 : 와이 델타 변환,Y-Δ 변환과 Δ-Y 변환, 변환 방정식, 예제 3개,활용
2. 노턴의 등가 회로(노턴의 정리)란?
노턴의 정리는 어떤 선형 네트워크든지 독립된 소스와 선형 저항으로 구성된 두 개의 단자를 가진 네트워크는 등가 회로로 대체될 수 있다는 것을 말합니다.
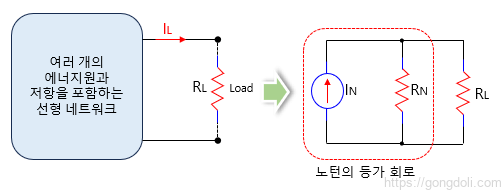
노턴의 등가 회로는 병렬 저항을 가진 전류원으로 구성됩니다.
노턴의 등가 회로의 전류원 크기는 부하 단자를 통해 흐르는 단락 전류와 같습니다.
그리고, 등가 저항은 주어진 회로에서 모든 소스가 내부 저항으로 대체될 때 부하 단자의 저항입니다.
아래 그림에서 볼 수 있듯이, 소스(전압 또는 전류 또는 둘 다)와 저항으로 이루어진 네트워크의 일부가 부하를 통해 흐르는 전류가 동일한 전류원과 병렬 저항으로 대체됩니다.
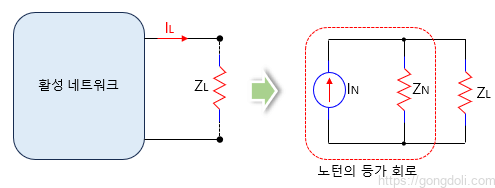
AC 회로의 경우, 독립된 소스와 임피던스로 구성된 어떤 활성의 두 단자 네트워크든지 등가 회로로 대체될 수 있습니다. 이 등가 회로는 병렬 임피던스를 가진 일정한 전류 원으로 구성됩니다.
전류 원의 값은 네트워크의 단락 단자를 통해 흐르는 전류와 동일하며, 병렬 임피던스는 모든 소스가 내부 임피던스로 대체될 때 단락 단자에서 본 등가 임피던스입니다.
이렇게 노턴의 정리는 복잡한 회로를 간단한 등가 회로로 대체함으로써 회로 분석을 단순화하고 효율적으로 수행할 수 있도록 돕습니다.
3.노턴의 등가 회로 분석 6단계
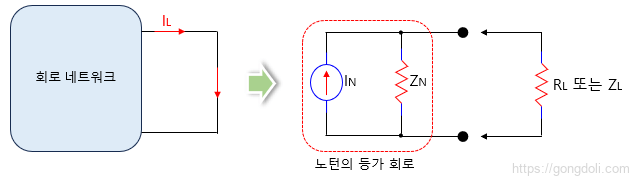
노턴의 정리를 사용하여 부하 변수를 찾기 위해서는 먼저 노턴의 등가 매개 변수를 결정해야 합니다.
이는 노턴 전류 또는 등가 전류원의 크기와 노턴 저항 Rn 또는 임피던스 ZN을 결정하는 것입니다.
이를 결정하기 위해 다음 단계를 수행해야 합니다.
1단계 : 부하 단자 단락 및 회로 분리
주어진 회로를 고려하고, 출력 또는 부하 단자에서 부하 저항(또는 AC 회로의 경우 임피던스)을 연결된 상태로 분리한 후 부하 단자를 단락시킵니다.
2단계 : 단락 단자를 통한 단락 전류 결정
단락된 단자를 통해 흐르는 단락 전류 IN을 결정합니다.
이는 메쉬 분석, 노달 분석 또는 수퍼포지션 정리와 같은 회로 축소 기법을 적용하여 측정할 수 있습니다.
또는 간단히 전류계를 사용하여 부하 전류를 실험적으로 측정할 수 있습니다.
3단계 : 회로 재구성
회로를 다시 그리고, 회로 내의 모든 실제 소스를 그들의 내부 전압 또는 단락 전압으로 대체하고 전류 소스를 단락시킵니다.
또한 부하의 단락된 단자를 열거나 제거하는 것을 잊지 않도록 합니다.
4단계 : 노턴 저항 계산
부하 단자로부터 본 저항(또는 임피던스)을 계산하여 부하 단자로부터 본 노턴 저항 RN 또는 (임피던스 ZN)을 구합니다.
5단계 : 등가 회로 구성
노턴의 등가 회로를 형성하는 전류 소스 IN과 병렬로 저항 (또는 임피던스)을 삽입합니다.
6단계 : 부하 변수 계산
부하를 노턴의 등가 회로에 다시 연결하고 부하와 관련된 전류, 전압 및 전력을 계산합니다.
DC 회로에서
- 부하 전류 IL = IN × [RN / (RL + RN)]
- 부하 전압 VL = IL × RL
- 부하에서 소비되는 전력 P = IL2 × RL
AC 회로에서
- 부하 전류 IL = IN × [ZN / (ZL + ZN)]
- 부하 전압 VL = IL × ZL
- 부하에서 소비되는 전력 P = IL2 × ZL
이렇게 단계별로 수행함으로써 노턴의 정리를 활용하여 부하의 전류, 전압 및 소비 전력을 효과적으로 계산할 수 있습니다.
4.노턴의 등가 회로 – 예제 풀이
노턴의 등가 회로는 이 “상수 전류”의 값은, 출력 단자 두 개를 짧게 연결할 때 흐르는 전류입니다.
이때 소스 저항은 단자로 돌아보았을 때 측정되며, 이는 Thevenin의 정리와 동일합니다.
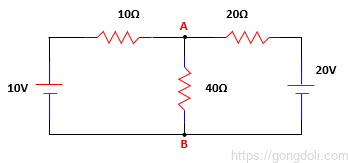
예를 들어,
위의 회로의 Nortons 등가 회로를 찾기 위해서는 먼저 중심에 연결된 40Ω 부하 저항을 제거하고, 단자 A와 B를 짧게 연결하여 다음과 같은 회로를 얻어야 합니다.
단자 A와 B가 짧게 연결되면, 두 저항이 각각의 전압 원본에 병렬로 연결되며, 각 저항을 흐르는 전류와 전체 단락 전류를 계산할 수 있습니다.
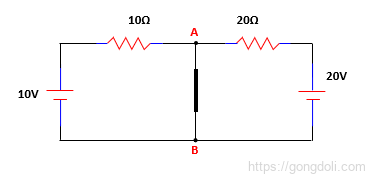
단자 A와 B가 단락되면 두 저항기가 각각의 두 전압원에 걸쳐 병렬로 연결되며 이제 전체 단락 전류뿐만 아니라 각 저항기를 통해 흐르는 전류를 다음과 같이 계산할 수 있습니다
Ishort_circuit = I1+I2
만약 두 전압 Source을 단락시키고 단자 A와 B를 Open한다면, 두 저항은 효과적으로 병렬로 연결됩니다.
내부 저항 Rs의 값은 단자 A와 B에서의 총 저항을 계산하여 구합니다.
이를 통해 우리는 다음과 같은 회로를 얻게 됩니다.
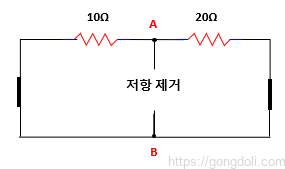
등가 내부 저항(Rs)은
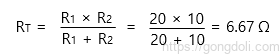
단락 전류 Is와 등가 내부 저항 Rs를 찾았으므로, 이제 다음과 같은 노턴의 등가 회로를 얻을 수 있습니다.
이제 원래의 40Ω 부하 저항이 단자 A와 B 사이에 연결된 상태에서 문제를 해결해야 합니다.
위의 그림에서 보듯이 다시 두 저항은 단자 A와 B 사이에 병렬로 연결됩니다.
이로 인해 총 저항은 다음과 같이 계산됩니다.
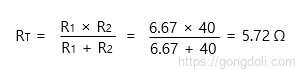
A와 B 단자 사이에 부하 저항이 연결되어 있을 때 단자 사이의 전압은 다음과 같이 주어집니다.

그런 다음 40Ω 부하 저항을 흐르는 전류를 찾을 수 있습니다.
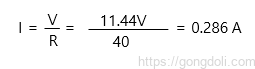
다시 한 번 Nortons의 정리를 사용하여, I3의 전류 값은 0.286A입니다.
5.노턴의 등가 회로(노턴의 정리)의 한계와 주의사항
노턴의 정리는 전기 회로 분석에 매우 유용하지만, 일부 경우에는 적용할 수 없거나 주의해야 할 사항이 있습니다.
5-1) 노턴의 정리가 적용되지 않는 경우
- 비선형 회로: 노턴의 정리는 선형 회로에만 적용됩니다.
비선형 요소가 있는 회로에는 적용할 수 없습니다. - 시간에 따라 변하는 회로: 노턴의 정리는 정상 상태인 회로에만 적용됩니다.
시간에 따라 전압이나 전류가 변하는 회로에는 적용할 수 없습니다. - 서로 의존적인 회로: 노턴의 정리는 독립적인 소스와 저항으로 이루어진 회로에만 적용됩니다.
서로 의존적인 요소가 있는 회로에는 적용할 수 없습니다.
5-2) 제약 사항과 주의사항
- 등가 회로의 정확성: 노턴의 정리를 사용하여 등가 회로를 찾을 때, 근사치로 계산되므로 정확성을 보장할 수 없습니다.
실제 회로 동작과 다를 수 있습니다. - 소스의 특성: 회로의 소스가 실제로는 상수 전류 소스가 아닐 수 있습니다.
이 경우 등가 회로의 정확성이 영향을 받을 수 있습니다. - 저항값의 변화: 회로의 온도, 습도, 주변 환경 등의 변화로 인해 저항값이 변할 수 있습니다.
이러한 변화는 등가 회로의 정확성에 영향을 줄 수 있습니다. - 회로 구성의 변경: 회로의 구성이 변경되거나 추가 요소가 추가될 경우, 기존에 계산한 등가 회로는 더 이상 유효하지 않을 수 있습니다.
따라서 회로 구성 변경 시에는 등가 회로를 다시 계산해야 합니다.
이러한 제약 사항과 주의사항을 고려하여 노턴의 정리를 적용할 때, 정확성과 신뢰성을 유지할 수 있습니다.
