능동 대역 통과 필터,동작 원리,회로, 반전 BPF, 예제1

1. 개요

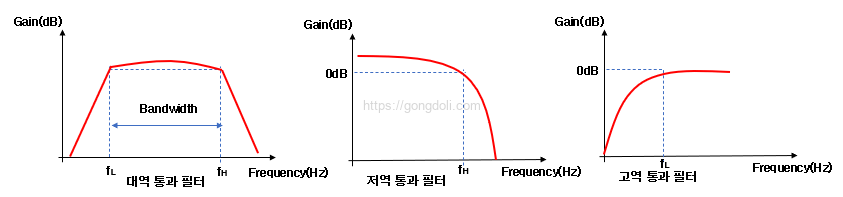
로우 패스 필터의 경우, 패스 밴드는 0Hz 또는 직류부터 시작하여 최대 패스 밴드 이득에서 -3dB 아래의 지정된 컷오프 주파수 지점까지 계속됩니다.
이와 같이, 하이 패스 필터의 경우 패스 밴드는 이 -3dB 컷오프 주파수부터 시작하여 무한대 또는 능동 필터의 최대 개방 루프 이득까지 지속됩니다.

그러나 능동 대역 통과 필터(Band Pass Filter)는 조금 다릅니다.
이것은 특정한 “대역”의 주파수 내에서 한 가지 특정 주파수의 신호를 분리하거나 해당 주파수 범위 내의 신호를 다른 모든 주파수의 신호로부터 분리하는 주파수 선택 필터 회로입니다.

이 대역 또는 주파수 범위는 “낮은 주파수” (ƒL)와 “높은 주파수” (ƒH)로 레이블이 지정된 두 개의 컷오프 또는 코너 주파수 지점 사이에 설정되며, 이 두 지점 외의 신호를 약화합니다.

간단한 능동 대역 통과 필터는 앞에서 언급한 단일 로우 패스 필터와 단일 하이 패스 필터를 연이어 연결하여 만들 수 있습니다.

로우 패스 필터 (LPF)의 컷오프 또는 코너 주파수가 하이 패스 필터 (HPF)의 컷오프 주파수보다 높으며, -3dB 지점에서의 주파수 간의 차이가 능동 대역 통과 필터의 “대역폭”을 결정하며, 이러한 지점 외의 신호를 약화합니다.
매우 간단한 능동 대역 통과 필터를 만드는 한 가지 방법은 앞에서 설명한 기본적인 패시브 고역 통과 필터와 저역 통과 필터를 증폭 오퍼레이션 앰프 회로에 연결하는 것입니다.

• 연관 참조 : RL 수동 저역 통과 필터, LPF 종류,동작 원리,상한 차단 주파수, 예제1
• 연관 참조 : 수동 RC 고역 통과 필터,Ideal,Real,주파수 응답,출력 전압 및 게인,예제1, 2차필터
• 연관 참조 : 수동 대역 통과 필터란?, RLC을 사용한 BPF회로,주파수 응답, 예제1,요약
• 연관 참조 : 능동 저역 통과 필터,1차 LPF, 전압 이득, 예제1
• 연관 참조 : 능동 고역 통과 필터,이상적인 HPF, 전압 이득, 주파수 응답
• 연관 참조 : 버터워스 필터, 주파수 응답, 근사화, 1차 LPF , 이상적인 주파수, 다항식

2. 능동 대역 통과 필터 회로

개별 저역 통과 필터와 고역 통과 필터를 연이어 연결하는 것은 넓은 패스 밴드를 가진 낮은 “Q-팩터” 유형의 필터 회로를 생성합니다.
저역 통과 필터는 입력 신호의 저주파수 구성 요소를 통과시키고 고역 통과 필터는 입력 신호의 고주파수 구성 요소를 통과시킵니다.
두 필터가 연이어 연결되면 입력 신호의 특정 주파수 대역을 통과시키는 패스 밴드가 형성됩니다.

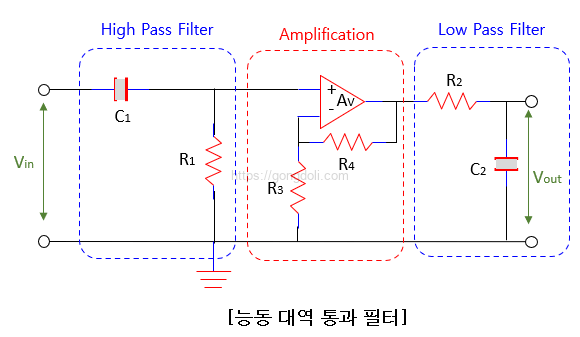
이 필터의 첫 번째 단계는 고역 통과 스테이지입니다.
이 스테이지에서는 캐패시터를 사용하여 원본 신호로부터의 직류 바이어스를 차단하고 고주파수를 통과시킵니다.
그 다음으로는 저역 통과 스테이지가 이어집니다.
이 스테이지에서는 고주파수를 차단하고 저주파수를 통과시킵니다.

이러한 구성의 장점은 중앙 주파수를 갖는 패스 밴드를 형성하면서 비교적 평평한 비대칭 패스 밴드 주파수 응답을 제공한다는 것입니다.
이 패스 밴드는 고역 통과 및 저역 통과 응답의 조합으로 이루어져 있으며, 패스 밴드 내의 주파수에 대해 대칭적이지 않을 수 있습니다.

높은 코너 포인트 (ƒH) 및 낮은 코너 주파수 컷오프 포인트 (ƒL)는 표준 1차 저역 통과 필터 및 고역 통과 필터 회로에서와 같은 방법으로 계산됩니다.
이러한 컷오프 포인트 사이의 합리적인 간격이 필요하며, 이는 두 스테이지 간의 상호 작용을 방지합니다.

또한, 증폭기는 두 스테이지 간의 격리를 제공하고 회로의 전체 전압 이득을 정의합니다.
따라서 필터의 대역폭은 상한과 하한 -3dB 포인트 간의 차이로 정의됩니다.
이를 통해 필터의 주파수 응답 범위를 결정할 수 있습니다.

예를 들어, -3dB 컷오프 포인트가 200Hz와 600Hz로 설정된 대역 통과

필터의 경우, 필터의 대역폭은 600Hz에서 200Hz를 뺀 400Hz가 됩니다.

3. 능동 대역 통과 필터 회로

수동 튜닝 필터 회로는 대역 통과 필터로 사용될 수 있지만, 종종 패스 밴드(대역폭)가 넓을 수 있습니다.
이것은 주파수 대역을 좁게 분리하려는 경우에 문제가 될 수 있습니다.
예를 들어, 특정 주파수 대역의 신호를 골라내거나 다른 주파수 대역의 잡음을 제거하려는 경우에는 보다 정확한 주파수 선택이 필요합니다.
이런 이유로 넓은 패스 밴드가 있는 수동 튜닝 필터는 항상 이상적이지 않을 수 있습니다.

능동 대역 통과 필터는 이러한 문제를 해결하기 위해 고안되었습니다.
이러한 필터는 인버팅 오퍼레이션 앰프를 사용하여 구성됩니다.
이를 통해 우리는 회로의 구성 요소를 재배열하고, 특정 주파수 대역을 강조하는 보다 정확한 필터 회로를 설계할 수 있습니다.

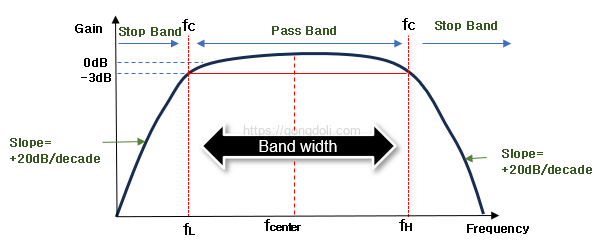
능동 대역 통과 필터의 동작 원리는 다음과 같습니다.
하위 컷오프 -3dB 포인트는 ƒ_L로 주어지며, 상위 컷오프 -3dB 포인트는 ƒ_H로 주어집니다.
이렇게하면 우리는 특정 주파수 범위 내에서 신호를 강화하고 다른 주파수를 차단할 수 있습니다.
이를 통해 더 정확하고 효과적인 주파수 선택이 가능해집니다.

능동 대역 통과 필터의 주요 특징 중 하나는 주파수 대역의 선택성입니다.
이 필터는 일정한 중심 주파수를 기준으로 주변 주파수를 허용하고 이외의 주파수를 차단합니다.
이러한 특성은 일종의 “차단 대역”과 “통과 대역”을 형성합니다.

이 필터의 주파수 응답은 일반적으로 패스밴드에서 최대 이득을 나타내며, 중심 주파수에서 멀어질수록 이득이 감소합니다.
이는 주파수가 필터의 패스밴드를 벗어나면 필터의 동작이 약화되는 것을 의미합니다.

3. 반전 능동 대역 통과 필터 회로

Inverting Band Pass Filter Circuit(반전 능동 대역 통과 필터 회로)는 입력 신호를 반전시키고 특정 주파수 대역을 강조하는 필터 회로입니다.
이 회로는 하이 패스 및 로우 패스 필터를 조합하여 사용되며, 증폭기(오퍼레이션 앰프)를 통해 신호를 증폭시킵니다.
하이 패스 필터와 로우 패스 필터의 순서가 중요하며, 이에 따라 패스 밴드의 특성이 결정됩니다.

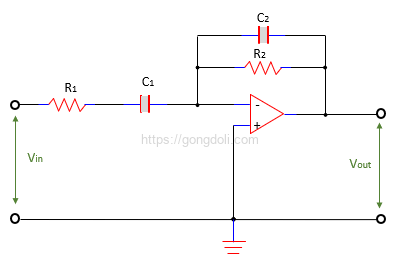
이 회로에서, 입력 신호는 하이 패스 필터를 통과하여 고주파 신호를 강조하고, 그 다음 로우 패스 필터를 통과하여 이 고주파 신호의 일부를 선택적으로 증폭합니다.
이를 통해 특정 주파수 대역의 신호를 강조하고 나머지 주파수를 차단합니다.

전압 이득은 필터 회로의 출력 전압과 입력 전압 간의 비율을 나타내는데, 이는 필터가 입력 신호를 얼마나 증폭시키는지를 나타냅니다.
능동 대역 통과 필터의 경우, 각각의 하이 패스 및 로우 패스 필터에는 전압 이득이 존재하며, 이를 통해 전체 필터 회로의 전압 이득을 계산할 수 있습니다.
일반적으로 전압 이득은 입력 신호의 주파수에 따라 변화하며, 이는 필터의 주파수 응답을 결정합니다.

전압 이득을 계산할 때는 각 필터 회로의 이득을 곱하여 전체 필터 회로의 전압 이득을 구할 수 있습니다.
능동 대역 통과 필터 회로의 전압 이득은 다음과 같은 수식으로 표현됩니다

∣V_out​/V_in​∣=−​R2/R1​​

• 여기서
• R1은 하이 패스 필터의 입력 저항이고,
• R2는 피드백 저항입니다.

이 수식은 기본적인 인버팅 OP Amp 회로의 전압 이득을 나타냅니다.

또한, 하이 패스 필터의 컷오프 주파수 f_c은 다음과 같이 정의됩니다

f_c1​=1/(2πR₁​C_1​)

f_c2​=1/(2πR₂​C_2​)

4. 대역 통과 필터 회로 예제풀이

전압 이득 Av가 1(1)이고 공진 주파수인 ƒr이 1kHz인 능동 대역 통과 필터는 무한 이득 다중 피드백 필터 회로를 사용하여 구성됩니다.
회로를 구현하는 데 필요한 구성 요소의 값을 계산해 보겠습니다.

• 회로의 이득(Av​)을 사용하여 품질 계수(Q)를 구합니다.
• R1​ 및 R2​의 저항값을 선택합니다.
• 공진 주파수(fr​)에 따라 필요한 캐패시터(C)의 값을 결정합니다.

4-1) 품질 계수(Q) 계산

대역 통과 필터의 품질 계수(Q)는 다음과 같은 공식을 사용하여 계산할 수 있습니다.

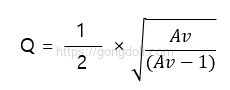
Av​=1로 주어진 경우, 다음과 같이 Q를 계산할 수 있습니다.

계산된 Q가 무한대이므로, 이는 필터의 대역폭이 좁다는 것을 나타냅니다.

4-2) 저항값 선택

Q=0.7071의 값을 가지는 경우, 저항 𝑅2​는 저항 𝑅1​의 두 배가 되는 관계를 갖습니다.

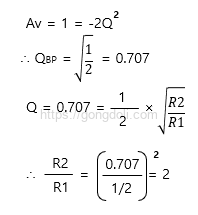
이 관계를 기반으로 적절한 저항 값을 선택합니다.
𝑅1=10 kΩ 및 𝑅2=20 kΩ로 선택합니다

4-3) 커패시터값 결정

공진 주파수(fr​)는 1 kHz로 주어집니다.
얻은 저항값을 사용하여 필요한 캐패시터(C)의 값을 결정할 수 있습니다.
캐패시터 값은 다음과 같은 공식을 사용하여 계산할 수 있습니다.

fr = 1000Hz = 1/2πC√R1R2

C=1/(2πfr​√R1R2​​)

=1/ {2π(1 kHz)×√10kΩ×20kΩ}

≈11.2 nF

가장 가까운 표준 캐패시터 값은 10 nF입니다.
따라서 C=10 nF를 선택할 수 있습니다.