데시벨(Decibel dB), 공식, 예제풀이, 종류 6가지,실생활에 비유

1. 데시벨(Decibel dB)란?

데시벨(decibel dB)은 소리, 전기 신호, 및 기타 물리적 양의 상대적인 크기를 표현하기 위해 사용되는 로그 스케일 단위입니다.
데시벨(Decibel dB)은 두 값 사이의 비율을 로그 함수로 나타내며, 상대적인 크기를 이해하고 비교하기 쉽게 합니다.
예를 들어, 소리의 크기를 데시벨(Decibel dB)로 표현하면 조용한 속삭임(약 30dB)부터 시끄러운 공장 소음(약 100dB)까지 모두 상대적으로 쉽게 비교할 수 있습니다.

데시벨의 기원은 전화 기술의 발달과 깊은 관련이 있습니다.
1920년대 미국 벨 연구소(Bell Telephone Laboratories)에서 처음 사용되기 시작했습니다.
데시벨은 원래 벨(bell)이라는 단위에서 파생되었으며, 전화 신호의 감쇠와 증폭을 측정하는 데 사용되었습니다.
벨이라는 단위는 알렉산더 그레이엄 벨(Alexander Graham Bell)의 이름을 따서 명명되었지만, 1 벨이 너무 큰 단위였기 때문에, 이를 1/10로 나눈 데시벨(Decibel dB)이 더 널리 사용되었습니다.

벨 연구소는 통신 시스템의 효율성을 분석하고, 신호의 손실과 증폭을 정확하게 측정할 필요가 있었습니다.
데시벨(Decibel dB)은 로그 스케일을 사용하여 큰 범위의 신호 변화를 쉽게 다룰 수 있게 해주었고, 이는 전화 네트워크의 성능 개선에 큰 기여를 했습니다.

이후 데시벨은 음향 공학, 전자공학, 통신공학 등 다양한 분야에서 널리 사용되기 시작했습니다.
그 이유는 데시벨(Decibel dB)이 상대적 크기를 비교하고, 시스템의 성능을 평가하며, 신호 손실을 분석하는 데 매우 효율적이기 때문입니다.

이와 같이 데시벨(Decibel dB)은 원래 통신 기술에서 시작되었지만, 현재는 다양한 분야에서 필수적인 단위로 자리 잡고 있습니다.
이를 통해 우리는 소리, 전기 신호, 에너지 등 여러 물리적 현상을 정확하고 효율적으로 이해하고 분석할 수 있습니다.

• 연관 참조 : dBm-W 변환 계산기,dBm-W conversion calculator,사용 방법

2. 데시벨(Decibel dB) 수학적 기초

2-1) 로그 스케일

로그 스케일은 숫자를 비교하고 표현할 때 큰 범위를 효과적으로 다룰 수 있게 해주는 수학적 도구입니다.
로그 스케일에서는 각 단위가 이전 단위보다 일정한 비율만큼 증가합니다.
예를 들어, 10의 로그 스케일에서는 1, 10, 100, 1000, … 과 같이 10배씩 증가합니다.
이는 수치가 기하급수적으로 증가할 때 그 차이를 명확히 하기 위해 사용됩니다.

데시벨(Decibel dB)은 로그 스케일을 사용하여 소리, 전기 신호 등 다양한 물리적 양의 상대적인 크기를 비교하는 단위입니다.
왜 로그 스케일을 사용하는지 이해하기 위해 소리 크기의 예를 들어 보겠습니다.
조용한 속삭임과 제트기 소음의 차이는 매우 큽니다.
이 두 소리의 에너지 차이는 약 10¹²(1조)배에 이르는데, 이를 일반적인 숫자로 표현하면 다루기 어렵습니다.
그러나 로그 스케일을 사용하면 이 큰 범위를 더 쉽게 비교하고 이해할 수 있습니다.

2-2) 데시벨 계산 공식

데시벨(Decibel dB) 값은 전력의 변화 수준을 비교하고 계산하는 비율로 사용됩니다.
예를 들어, P1과 P2라는 두 가지 전력이 있다고 가정해보겠습니다.
이 두 값의 비율은 다음과 같은 방정식으로 표현됩니다.

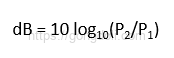
• 여기서,
• P1은 입력 전력
• P2는 출력 전력

데시벨(Decibel dB)은 두 전력 수준의 로그 변화를 나타내므로 이 방정식을 더 확장하여 한 데시벨(1dB)이 얼마나 많은 변화를 나타내는지 알 수 있습니다.

만약 입력 전력과 출력 전력이 같다면 (즉, P1 = P2), 데시벨 계산식에 대입하여 값을 계산할 수 있습니다.
이 경우, P2/P1의 값은 1이 됩니다.

dB = 10 log₁₀(1) = log₁₀(1/10) = log₁₀(0.1) = antilog(0.1)

그러므로 값의 1dB 변화는 10^0.1 = 1.259

따라서 두 전력의 로그 변화는 1.259의 비율을 갖게 됩니다.
이는 1dB의 변화가 전력의 25.9% 증가 (또는 감소)를 의미합니다.

따라서, 예를 들어 회로나 시스템의 이득이 5 (7dB)이라면, 이를 26% 증가시킨다면, 회로의 새로운 전력 비율은 다음과 같을 것입니다

5*1.26 = 6.3, 따라서 10 log₁₀(6.3) = 8dB가 됩니다.

이는 1dB의 이득이 전력의 26%의 로그 증가를 나타내며, 이는 선형적인 변화가 아닌 로그 스케일로 표현된 것임을 보여줍니다.

2-3) 예제 풀이

오디오 증폭기에 100mW의 입력 신호로 공급되었을 때 8 Ω 스피커 부하에 100 W의 출력을 제공합니다.
증폭기의 전력 이득을 데시벨로 계산해 보겠습니다.

먼저 주어진 값은

• 출력 전력 (P2) = 100 W
• 입력 전력 (P1) = 100 mW = 0.1 W

이제 전력 이득을 계산해 보겠습니다.

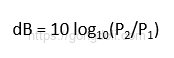
= 10 log₁₀(100/0.1)
= 10 log₁₀(1000)
= 10 × 3 = 30 dB

따라서, 이 증폭기의 전력 이득은 30 dB입니다.

만약 100W의 오디오 증폭기는 전력 이득 비율이 30dB입니다.
그렇다면 그의 최대 입력 값은 얼마가 되는지 계산해 보겠습니다.

전력 이득 비율은 다음과 같이 정의됩니다.

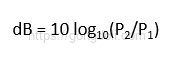
주어진 전력 이득 비율은 30dB이며, 출력 전력은 100 W입니다.

따라서 입력 전력을 구하려면

30dB = 10 log₁₀(100/P1)

먼저 두 변에 10을 나누어 제거합니다.

3 = log₁₀(100/P1)

그런 다음 지수 함수를 취해 로그를 제거합니다.

10³ = 100/P1

1000 = 100/P1

이제 입력 전력을 구하기 위해 방정식을 해결합니다.

P1 = 100/1000 = 0.1 W

따라서, 오디오 증폭기의 최대 입력 값은 0.1 W입니다.

3. 데시벨(Decibel dB) 종류

3-1) dBm

dBm은 전기적인 전력 수준을 나타내는 측정 단위입니다.
이는 1mW에 대한 참조를 가지며, 0 dBm은 1 mW에 해당합니다.
이 측정 단위는 전압이나 임피던스와 직접적인 관련이 없습니다.
1940년대에는 산업 표준으로 사용되었습니다.

이 측정 단위가 처음 개발될 때, 주로 600 Ω 전화선을 측정하는 데 사용되었습니다.
그 시기에 전력은 항상 0.001 W이며, 임피던스는 600 Ω이었기 때문에, 시스템 전압은 정확히 0.775 V rms였습니다.
이로 인해 많은 사람들이 0 dBm의 기준을 0.775 V와 혼동하게 되었습니다.
하지만 이는 600 Ω일 때만 해당됩니다

예를 들어, 프리앰프의 최대 출력이 +30 dBm이라면, 이를 해석해 보겠습니다.
+10 dBm은 출력을 열 배로 증가시킵니다.

• 따라서
• – 0 dBm은 0.001 와트를 의미합니다.
• – +10 dBm은 0.01 와트를 의미합니다.
• – +20 dBm은 0.1 와트를 의미합니다.
• – +30 dBm은 1 와트를 의미합니다.

또한 다음과 같은 공식을 사용하여 이를 계산할 수 있습니다.

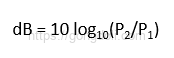
따라서, +30 dBm의 경우, 이를 공식에 대입하면 다음과 같이 됩니다.
30 = 10 * log(P2 / 0.001)
이를 풀면, P2 = 1 W가 됩니다.

3-2) dBu decibel

dBu 데시벨은 전압의 측정 단위로, 주로 오디오 장비에서 사용됩니다.
이는 전압 레벨에 대한 측정이며, 이전에 사용되던 dBm과는 달리 전력 레벨이 아니라 전압 레벨에 초점을 맞추고 있습니다.
dBu는 전압의 상대적인 크기를 나타내는데, 0 dBu는 0.775 V를 기준으로 합니다.

예를 들어, +20 dBu의 경우를 살펴보겠습니다. 이는 전압을 10배로 증폭하는 것을 의미합니다.
따라서, 0 dBu는 0.775 V를 의미하므로, +20 dBu는 0.775 V를 10배로 증폭한 7.75 V를 나타냅니다.

이를 계산하는 또 다른 방법은 다음과 같은 공식을 사용하는 것입니다.
dB = 20 * log10(E1 / 0.775)

여기서 ( E1 )은 특정 전압을 나타냅니다.
따라서, +20 dBu의 경우, 이를 공식에 대입하면 다음과 같이 됩니다.
20 = 20 * log10(E1 / 0.775)

이를 풀면 E1 = 7.75 V가 됩니다.

3-3) dBv and dBV

dBv와 dBV는 모두 전압을 측정하는 데 사용되는 단위입니다.
그러나 각각의 참조값이 다르며, 이는 계산에 영향을 줍니다.
dBv는 0 dBv가 0.775V를 의미하며, 주로 오디오 시스템에서 사용됩니다.
이는 오디오 장비의 전압 레벨을 측정하고 비교하는 데 유용합니다.

한편, dBV는 dBv와 다르게 전압의 참조값이 1 V입니다.
즉, 0 dBV는 1 V를 의미합니다.
dBV는 주로 전압의 정확한 측정이 필요한 곳에서 사용됩니다.

예를 들어, 출력 레벨이 +4 dBv / dBV인 경우를 살펴보겠습니다.
이 경우, dBv와 dBV의 계산 방식은 서로 다릅니다.

dBv의 경우, 다음과 같은 공식을 사용하여 계산합니다.

4 = 20 * log(E1 / 0.775)
여기서 E1 은 입력 전압을 나타냅니다.

이를 풀면 E1 = 1.23 V가 됩니다.

반면에 dBV의 경우, 다음과 같은 공식을 사용하여 계산합니다.
4 = 20 * log(E1 / 1)
이를 풀면 E1 = 1.6 V가 됩니다.

3-4) dBW

dBW는 전력과 관련된 참조점을 가진 데시벨(Decibel dB)의 한 유형입니다.
dBm과 유사하지만, 참조 전력이 다릅니다.
dBm은 주로 저전력 출력을 설명하는 데 사용됩니다.

예를 들어, 마이크로폰이나 신호 처리기와 같은 장치에서 사용됩니다.
이러한 장치들은 출력 전력이 매우 낮기 때문에, dBm 단위가 적절합니다.
dBm의 참조점은 0 dBm = 0.001 W입니다.

하지만 고출력 장치, 예를 들어 전력 증폭기와 같은 경우에는 dBm 단위가 적절하지 않을 수 있습니다.
이러한 장치들은 훨씬 더 높은 출력 전력을 가지기 때문에, 더 큰 단위가 필요합니다.
이러한 상황에서 사용되는 것이 dBW입니다.
dBW의 참조점은 0 dBW = 1 W입니다.

이를 통해, 고출력 장치의 출력을 측정할 때 dBW 단위가 더 유용하게 사용될 수 있습니다.
예를 들어, 1000 W의 출력을 가지는 전력 증폭기의 출력 전력을 dBm으로 표현하면 매우 큰 숫자가 나오게 됩니다.
반면, dBW를 사용하면 훨씬 더 다루기 쉬운 숫자로 표현할 수 있습니다.

예를 들어, 1000 W의 출력을 dBW로 표현하면 다음과 같습니다
0 dBW = 1 W
10 dBW = 10 W
20 dBW = 100 W
30 dBW = 1000 W

이와 같이, dBW는 고출력 전력 측정에 더 적합한 단위입니다.
dBm이 저출력 전력을 다루는 데 적합한 것처럼, dBW는 고출력 전력을 다루는 데 적합합니다.

3-5) dB SPL

이것은 데시벨(Decibel dB)을 계산하는 방법 중 음향에 관련된 부분입니다.
여기서는 소리 압력 수준(SPL)을 설명합니다.
SPL은 소리 압력 수준을 의미하며, 이는 전압 비율과 어느 정도 관련이 있습니다.

전압의 또 다른 용어는 전자기력(EMF)입니다.
고막이나 마이크 다이어프램에 대한 공기의 압력은 배터리가 회로의 저항에 전자를 밀어내는 힘과 유사합니다.
따라서, dB 전압과 마찬가지로, 소리 압력 수준 비율의 공식은 다음과 같습니다.

dBSPL = 20 * log(P1 / P0)

여기서 P1과 P0는 소리 압력(N/m² 단위)입니다.

이제 우리는 SPL 데시벨을 계산하는 방법을 배웠으므로 몇 가지 결론을 도출할 수 있습니다.
이 공식은 +6 dB마다 소리 압력이 두 배가 되고, +20 dB일 때 소리 압력이 열 배가 된다는 것을 알려줍니다.

하지만 우리는 SPL을 어떻게 인식할까요?
실제로는 종이에 쓴 것처럼 간단하지 않습니다.
+3 dB의 차이는 거의 더 크게 들리지 않으며, 소리가 두 배 더 크게 들리려면 +10 dB 더 높아야 합니다.
소리의 크기는 주관적인 양이며, 주파수와 절대 소리 수준에 따라 다릅니다.

다른 데시벨 유형과 마찬가지로, dB SPL도 참조 기준이 있습니다.
이는 0 dB SPL로, 청력의 역치로도 알려져 있습니다.
젊고 손상되지 않은 귀에서는 이를 완전한 침묵으로 인식해야 하며, 이는 0.000002 N/m²로 측정됩니다.

예를 들어, 일반적인 소리의 근원과 그들의 대략적인 dB SPL 등급을 살펴보겠습니다.

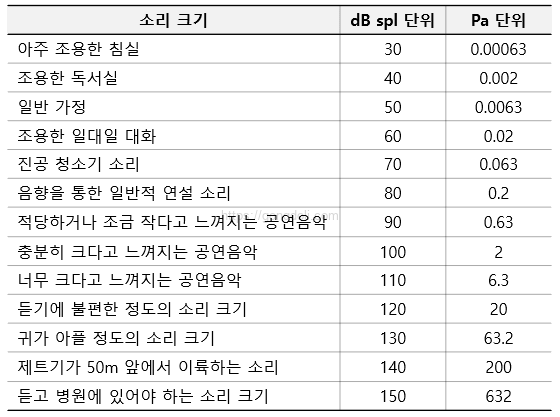
이와 같은 척도는 일상에서 우리가 접하는 소리들의 크기를 이해하는 데 도움을 줍니다.
SPL은 청각 보호와 관련된 중요한 지표입니다.
예를 들어, 85 dB SPL 이상의 소음에 장시간 노출되면 청력 손상이 발생할 수 있으므로, 귀마개와 같은 보호 장비를 사용하는 것이 중요합니다.

이제 SPL을 실제 생활에서 어떻게 계산하고 적용하는지에 대한 예를 살펴보겠습니다.
만약 어떤 기기가 0.1 N/m²의 소리 압력을 발생시키고, 참조 압력 P0가 0.000002 N/m²라면, 이 기기의 SPL을 계산할 수 있습니다.

SPL = 20 * log(0.1 / 0.000002) = 20 * log(50000) = 20 * 4.699 = 약 94 dB

이 예에서 볼 수 있듯이, 계산 결과로 얻은 94 dB는 매우 큰 소리입니다.
이는 우리가 록 콘서트에서 경험하는 소리 수준과 비슷합니다.

3-6) dB PWL

dB PWL은 음향 파워를 측정하는데 사용되며, 이는 음향 와트로 표현됩니다.
음향 파워는 폐쇄된 공간의 반향 시간이나 스피커의 효율성을 계산할 때 사용됩니다.

이것은 전력 비율을 나타내므로 dBm과 유사한 공식을 사용합니다.
다음은 dB PWL을 계산하는 방법입니다

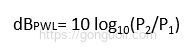
여기서, P2/P1은 음향파워를 나타냅니다.

스피커 제조업체는 스피커의 효율성을 dB SPL 효율성 평가로 인용하는 경우가 많습니다.
dBW와 음향 와트 (dB PWL) 사이의 관계에는 명확한 규칙이 없지만, 실제 값들을 자세히 살펴보면 스피커 시스템의 효율성을 파악할 수 있습니다.

예를 들어, 스피커에 20 dBW를 공급하면, 음향적으로는 10 dB PWL만 생성될 수 있습니다.
이를 와트로 번역하면, 100 와트의 전력이 들어가도 음향 파워로는 10 와트만 생성될 수 있다는 것을 의미합니다.
이는 스피커의 효율성이 10%라는 것을 나타내며, 실제로는 베이스 반사형 장치에 대한 스피커의 효율성이 높다는 것을 시사합니다.

4. 데시벨(Decibel dB)을 실생활에 비유

데시벨(Decibel dB) 개념을 이해하기 위해 실생활 비유를 사용하는 것은 매우 유용합니다.

4-1) 소리의 크기

소리의 크기를 데시벨(Decibel dB)로 측정하는 것은 흔한 예입니다.
조용한 방의 소음 수준은 약 30dB, 일반적인 대화 소리는 약 60dB, 콘서트나 클럽에서는 110dB 이상이 될 수 있습니다.
데시벨(Decibel dB)은 로그 스케일을 사용하기 때문에, 10dB 증가하면 소음의 강도가 10배 증가합니다.

4-2) 거리의 비유

100미터 떨어진 곳에 있는 사람에게 말하는 것과 바로 옆에 있는 사람에게 말하는 것을 비교해 보겠습니다.
100미터 거리에서 대화를 나누려면 소리를 매우 크게 내야 하지만, 바로 옆에 있을 때는 아주 작은 소리로도 대화가 가능합니다.
이처럼 소리의 강도는 거리와 비례하여 급격히 변화합니다.
데시벨(Decibel dB)도 마찬가지로 작은 변화가 큰 차이를 만듭니다.

4-3) 전력 증폭기

전력 증폭기를 사용하는 예를 들어보겠습니다.
가정용 오디오 시스템의 앰프는 보통 몇 와트의 출력을 가집니다.
예를 들어, 앰프의 출력이 100와트라고 가정하면, 이는 +20dBm에 해당합니다.
이 앰프에 입력 신호가 1mW일 때, 출력 신호는 100와트로 증폭됩니다.
이는 100,000배 증가한 것이며, 데시벨(Decibel dB)로는 50dB 증가한 것입니다.