1. 드모르간의 법칙이란?
드모르간의 법칙은 논리 대수(또는 부울 대수)의 기본적인 법칙 중 하나로, 논리 연산의 부정을 다루는 중요한 규칙입니다.
이 법칙은 복잡한 논리식을 단순화하고, 디지털 회로 설계에서 최적화하는 데 필수적인 도구입니다.
1-1) 드모르간의 법칙의 정의와 소개
드모르간의 법칙은 19세기 수학자 어거스터스 드 모르간(Augustus De Morgan)에 의해 소개된 논리 대수의 두 가지 규칙으로 구성됩니다.
이 법칙은 논리 연산자 AND와 OR의 부정을 통해서 관계를 나타냅니다.
드모르간의 법칙은 두 가지 형태로 존재합니다.
1-1-1) 첫 번째 법칙
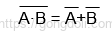
이 법칙은 두 입력 A와 B가 AND 연산으로 결합된 경우, 그 결과의 부정은 각각의 입력을 개별적으로 부정하고 OR 연산으로 결합한 것과 같음을 나타냅니다.
1-1-2) 두 번째 법칙
이 법칙은 두 입력 A와 B가 OR 연산으로 결합된 경우, 그 결과의 부정은 각각의 입력을 개별적으로 부정하고 AND 연산으로 결합한 것과 같음을 나타냅니다.
이 두 법칙은 논리식의 부정을 처리하는 데 중요한 역할을 하며, 복잡한 논리식을 단순화하는 데 유용합니다.
예를 들어, 논리 회로를 설계할 때 드모르간의 법칙을 사용하면 필요한 게이트 수를 줄이고, 회로의 효율성을 높일 수 있습니다
1-2) 논리 대수와 디지털 회로에서의 중요성
드모르간의 법칙은 논리 대수와 디지털 회로 설계에서 매우 중요합니다. 논리 대수는 컴퓨터 과학과 전자 공학에서 논리 연산을 다루는 기초적인 이론으로, 디지털 회로의 동작 원리를 설명합니다.
디지털 회로는 컴퓨터와 대부분의 전자 장치에서 사용되며, 기본적으로 논리 게이트로 구성되어 있습니다.
드모르간의 법칙은 다음과 같은 이유로 중요한 역할을 합니다.
1-2-1) 논리식의 단순화
드모르간의 법칙을 사용하면 복잡한 논리식을 단순화할 수 있습니다.
복잡한 식을 단순화하면, 더 적은 논리 게이트를 사용하여 동일한 기능을 구현할 수 있습니다.
이는 회로 설계의 효율성을 높이고, 비용을 절감하는 데 도움이 됩니다.
예를 들어, 다음과 같은 논리식을 고려해 보겠습니다.
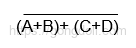
드모르간의 법칙을 적용하면, 이 식은 다음과 같이 변환됩니다.
이 변환을 통해 복잡한 논리식을 더 간단하게 만들 수 있습니다.
1-2-2) 회로의 최적화
디지털 회로 설계에서, 드모르간의 법칙은 회로를 최적화하는 데 사용됩니다.
논리 게이트의 수를 줄이고, 필요한 회로 면적을 감소시킬 수 있습니다.
이는 특히 대규모 집적 회로(VLSI) 설계에서 중요합니다.
효율적인 회로는 전력 소비를 줄이고, 성능을 향상시킬 수 있습니다.
예를 들어, NOT 게이트와 AND 게이트를 사용하여 NAND 게이트를 구현할 수 있습니다.
드모르간의 법칙을 사용하면, OR 게이트와 NOT 게이트를 사용하여 동일한 기능을 수행할 수 있는 NAND 게이트를 설계할 수 있습니다.
1-2-3) 프로그래밍에서 조건문 최적화
드모르간의 법칙은 프로그래밍에서 조건문을 최적화하는 데에도 유용합니다.
복잡한 조건문을 간단하게 변환하면, 코드의 가독성을 높이고 유지보수를 용이하게 할 수 있습니다.
예를 들어, 다음과 같은 조건문이 있다고 가정해 보겠습니다.
드모르간의 법칙을 적용하면, 이 조건문은 다음과 같이 변환될 수 있습니다.
이 변환은 코드의 이해를 더 쉽게 만들 수 있습니다.
드모르간의 법칙은 논리 대수의 기본 원칙 중 하나로, 디지털 회로 설계와 프로그래밍에서 매우 중요한 도구입니다.
이 법칙을 잘 이해하고 활용하면, 복잡한 논리식을 더 쉽게 다루고, 회로와 코드의 효율성을 크게 향상시킬 수 있습니다.
- 연관 참조 : NAND 게이트 회로, 회로 구성, 특성과 성능, 장점 4개와 한계
- 연관 참조 : NOR 게이트 회로, 회로 구성, 특성 및 성능, 장점 3개와 한계
- 연관 참조 : XOR 게이트 회로 설계, 회로 구성, 특성 및 성능, 장점 3개와 한계
- 연관 참조 : XNOR 게이트 회로, 회로 구성, 특성과 성능, 장점 4개와 한계
- 연관 참조 : Buffer 회로 설계, 회로 설계의 기본 구성, 설계 고려 사항
- 연관 참조 : 부울 대수 법칙, 기본 연산 AND,OR,NOT, 예제 2개 풀이
2. 드모르간의 첫 번째 법칙
드모르간의 법칙은 논리 대수에서 매우 중요한 역할을 하는 두 가지 기본 법칙으로, 복잡한 논리식을 단순화하고 회로 설계를 최적화하는 데 사용됩니다.
2-1) AND 연산의 부정과 OR 연산의 관계
드모르간의 첫 번째 법칙은 다음과 같습니다.
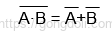
법칙은 논리식에서 AND 연산의 부정이 OR 연산의 부정과 어떻게 관계되는지를 설명합니다.
- AND 연산의 부정: 두 입력 A와 B의 AND 연산 결과를 부정한다는 것은,
A와 B가 모두 참인 경우 거짓이 된다는 것을 의미합니다. - OR 연산의 부정: 각 입력 A와 B를 각각 부정한 후 OR 연산을 한다는 것은,
A 또는 B 중 하나라도 거짓일 때 참이 된다는 것을 의미합니다.
드모르간의 첫 번째 법칙은 이러한 두 표현이 논리적으로 동일함을 보여줍니다.
즉, 두 입력의 AND 연산 결과를 부정하는 것은, 각각의 입력을 부정한 후 OR 연산을 수행하는 것과 같습니다.
이 법칙을 직관적으로 이해하기 위해, 논리적 상황을 예로 들어 설명해 보겠습니다.
이렇게 드모르간의 첫 번째 법칙은 AND 연산의 부정과 OR 연산의 부정 사이의 관계를 명확히 설명해 줍니다.
2-2) 수학적 표현과 예제
드모르간의 첫 번째 법칙은 수학적으로 다음과 같이 표현됩니다.
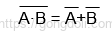
이 수식은 논리 회로 설계나 컴퓨터 프로그램에서 복잡한 논리식을 단순화하는 데 유용하게 사용됩니다.
실제 예제를 통해 이 법칙을 적용해 보겠습니다.
2-2-1) 예제 1: 논리식의 단순화
2-2-2) 예제 2: 디지털 회로 설계
디지털 회로에서, 드모르간의 법칙을 사용하여 NAND 게이트를 다른 게이트로 대체할 수 있습니다.
예를 들어, NAND 게이트로 구성된 다음 회로를 보겠습니다.
이 출력을 드모르간의 첫 번째 법칙을 사용하여 변환하면
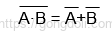
이 식은 NAND 게이트를 사용하지 않고도 NOT 게이트와 AND게이트를 사용하여 동일한 기능을 구현할 수 있음을 의미합니다.
회로에서, 드모르간의 법칙을 활용하여 필요한 게이트 수를 줄이거나, 특정한 논리 게이트를 대체하여 회로를 더 간단하고 효율적으로 만들 수 있습니다.
3. 드모르간의 두 번째 법칙
드모르간의 두 번째 법칙은 OR 연산의 부정과 AND 연산의 부정 사이의 관계를 설명합니다.
3-1) OR 연산의 부정과 AND 연산의 관계
드모르간의 두 번째 법칙은 다음과 같습니다.
이 법칙은 논리식에서 OR 연산의 부정이 AND 연산의 부정과 어떻게 관계되는지를 설명합니다.
- OR 연산의 부정: 두 입력 A와 B의 OR 연산 결과를 부정한다는 것은,
A 또는 B 중 하나라도 참이면 거짓이 되고, 둘 다 거짓일 때 참이 된다는 것을 의미합니다. - AND 연산의 부정: 각각의 입력 A와 B를 부정한 후 AND 연산을 한다는 것은,
A가 거짓이고 B가 거짓일 때 참이 된다는 것을 의미합니다.
드모르간의 두 번째 법칙은 이러한 두 표현이 논리적으로 동일함을 보여줍니다.
즉, 두 입력의 OR 연산 결과를 부정하는 것은, 각각의 입력을 부정한 후 AND 연산을 수행하는 것과 동일합니다.
이 법칙을 직관적으로 이해하기 위해, 논리적 상황을 예로 들어 설명해 보겠습니다.
이렇게 드모르간의 두 번째 법칙은 OR 연산의 부정과 AND 연산의 부정 사이의 관계를 명확히 설명해 줍니다.
3-2) 수학적 표현과 예제
드모르간의 두 번째 법칙은 수학적으로 다음과 같이 표현됩니다.
이 수식은 논리식과 회로를 단순화하는 데 매우 유용합니다. 실제 예제를 통해 이 법칙을 적용해 보겠습니다.
3-2-1) 예제 1: 논리식의 단순화
3-2-2) 예제 2: 디지털 회로 설계
디지털 회로에서, 드모르간의 법칙을 사용하여 NOR 게이트를 다른 게이트로 대체할 수 있습니다.
예를 들어, NOR 게이트로 구성된 다음 회로를 보겠습니다.
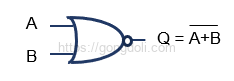
이 출력을 드모르간의 두 번째 법칙을 사용하여 변환하면
이 식은 NOR 게이트를 사용하지 않고도 NOT 게이트와 OR 게이트를 사용하여 동일한 기능을 구현할 수 있음을 의미합니다.
회로에서, 드모르간의 법칙을 활용하여 필요한 게이트 수를 줄이거나, 특정한 논리 게이트를 대체하여 회로를 더 간단하고 효율적으로 만들 수 있습니다.