Contents
1. 메쉬 전류 분석 개요
전기 회로를 분석하는 데 사용되는 메쉬 전류 분석은 복잡한 회로를 해석하고 이해하는 데 도움이 되는 중요한 도구입니다.
이 방법은 회로에서 전류의 흐름을 이해하고 예측하는 데 중점을 둡니다.
전기 회로는 다양한 전기적 구성 요소로 구성되어 있으며, 이러한 요소들 사이의 전류와 전압은 다양한 상황에서 상호 작용합니다.
이러한 상호 작용을 이해하고 예측하기 위해 회로 분석 기법이 필요합니다.
메쉬 전류 분석은 회로의 복잡성을 이해하고 각 부분의 동작을 예측하는 데 매우 유용합니다.
메쉬 전류 분석은 특히 복잡한 회로에서 효과적으로 사용됩니다.
복잡한 회로에서는 다양한 전류가 서로 교차하고 복잡하게 연결될 수 있습니다.
메쉬 전류 분석은 이러한 상황에서 전류의 흐름을 효율적으로 이해하고 예측하는 데 도움이 됩니다.
메쉬 전류 분석은 회로 설계, 문제 해결 및 실제 회로의 동작을 이해하는 데 필수적인 도구입니다.
이를 통해 전기 공학자들은 회로를 효과적으로 설계하고 문제를 해결하는 데 필요한 정보를 얻을 수 있습니다.
- 연관 참조 : 키르히호프의 회로 법칙, KCL, KVL, 예제, KCL vs. KVL,적용과 한계
- 연관 참조 : 오옴의 법칙 원리, 개념, 예제로 이해하기,전력 구하기,파이 차트
- 연관 참조 : 노드 전압 분석, 분석 방법 5단계, 예제, 메쉬 전류 분석과 비교
- 연관 참조 : 테브난의 정리, 5단계 방법, 예제, 한계와 주의 사항
- 연관 참조 : 노턴의 등가 회로, 정의, 분석 6단계, 예제, 한계와 주의 사항
- 연관 참조 : 밀만의 정리, 등가 회로, 예제,옴의 법칙과 키르히호프 법칙과 비교,한계
2. 매쉬 전류 분석이란?
2-1) 메쉬 전류 분석이나 노드 전압 분석을 사용하는 이유?
Kirchhoff의 법칙은 복잡한 전기 회로를 분석하는 기본적인 방법을 제공하지만, Mesh Current Analysis 또는 Nodal Voltage Analysis를 사용하여 이 방법을 개선하는 다양한 방법이 있습니다.
이러한 방법은 수학적 계산량을 줄여주어 다양하게 연결된 저항을 분석할 때 매우 유용합니다.
예를 들어,
전기 회로를 분석하는 데 있어서 기본적인 방법으로는 Kirchhoff의 전류 법칙과 전압 법칙을 사용합니다.
이 방법은 전기 회로의 복잡성을 이해하고 전류와 전압의 관계를 파악하는 데 도움이 됩니다.
그러나 이러한 방법은 큰 규모의 회로에서는 많은 수학적 계산이 필요하고 복잡해질 수 있습니다.
매쉬 전류 분석(Mesh Current Analysis) 또는 Nodal Voltage Analysis와 같은 방법은 전류와 전압의 관계를 더 쉽게 이해할 수 있도록 도와줍니다.
매쉬 전류 분석(Mesh Current Analysis)는 전기 회로를 메쉬(순환 경로)로 나누고, 각 메쉬에서의 전류를 변수로 설정하여 회로를 분석합니다.
이렇게 하면 전체 회로를 더 작은 부분으로 나누어서 이해하기 쉽고, 계산량도 줄일 수 있습니다.
Nodal Voltage Analysis는 노드(접점)를 기준으로 회로를 분석합니다.
각 노드에서의 전압을 변수로 설정하여 회로의 전압을 계산합니다.
이 방법은 전압을 중심으로 회로를 분석하기 때문에 전압에 관련된 문제를 더 쉽게 해결할 수 있습니다.
이러한 분석 방법을 사용하면 복잡한 회로도 더 효율적으로 분석할 수 있습니다,
2-2) 메쉬 전류 회로 분석
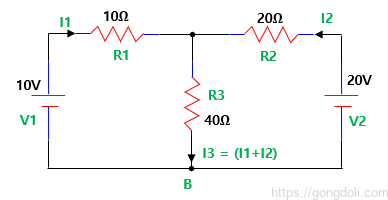
2-2-1) 키르히호프의 법칙으로 단순화하면,
수학적 계산량을 줄이는 하나의 간단한 방법은 회로를 분석할 때 Kirchhoff의 전류 법칙 방정식을 사용하여 두 저항에 흐르는 전류인 I1과 I2를 결정하는 것입니다.
그런 다음 I3의 전류를 계산할 필요가 없으므로, I3는 단순히 I1과 I2의 합이 됩니다.
그러므로 Kirchhoff의 두 번째 전압 법칙은 다음과 같이 단순화됩니다
방정식 1 : 10 = 50×I1 + 40×I2
방정식 2 : 20 = 40×I1 + 60×I2
결과적으로, 한 줄의 수학적 계산이 줄어들었습니다.
이러한 접근법은 복잡한 회로에서도 효과적으로 사용될 수 있습니다.
전체 회로를 분석하는 대신 각 부분의 전류를 분석함으로써, 수학적 계산량을 줄이고 전체적인 분석 과정을 간소화할 수 있습니다.
2-2-2) 메쉬 전류 분석으로 더욱 간편하게,
위의 회로를 해결하는 더 간편한 방법은 메쉬 전류 분석 또는 루프 분석을 사용하는 것입니다.
이 방법은 때로는 맥스웰의 순환 전류 방법(Maxwell´s Circulating Currents)이라고도 불립니다.
이 방법은 각 “닫힌 루프”에 순환 전류를 labelling하는 것으로 시작합니다.
일반적인 원칙으로, 회로 내의 각 루프에는 시계방향으로만 순환 전류를 라벨링하는 것이 좋습니다.
목적은 회로의 모든 요소를 최소한 한 번 이상 커버하는 것입니다.
필요한 분기 전류는 이전과 같이 Kirchhoff의 방법을 사용하여 해당 루프 또는 메쉬 전류에서 찾을 수 있습니다.
예를 들어,
i1= I1, i2=-I2, 그리고 I3 = I1-I2 입니다.
이제 이전과 같은 방법으로 Kirchhoff의 전압 법칙 방정식을 작성하여 해결할 수 있지만, 이 방법의 장점은 회로 방정식에서 얻은 정보가 회로를 해결하는 데 필요한 최소한의 정보임을 보장한다는 것입니다.
이 정보는 보다 일반적이며 행렬 형태로 쉽게 나타낼 수 있습니다.
이러한 방정식은 단일 메쉬 임피던스 행렬 Z를 사용하여 매우 빠르게 해결할 수 있습니다.
주 대각선 상의 각 요소는 “양수”이며 각 메쉬의 총 임피던스입니다.
그와 반대로, 주 대각선에서 벗어난 각 요소는 “영” 또는 “음수”이며 모든 적절한 메쉬를 연결하는 회로 요소를 나타냅니다.
우선, 행렬을 다룰 때 두 행렬의 나눗셈은 서로의 역행렬을 곱하는 것과 같다는 점을 이해해야 합니다.
이것은 다음과 같이 나타낼 수 있습니다.
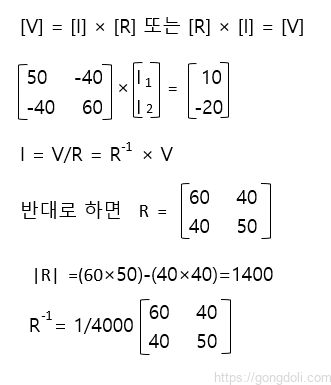
V/R이 Vx R-1과 같으므로 R의 역수를 구하면

- 여기서,
[ V ] 루프 1과 루프 2의 총 배터리 전압을 제공.
[ I ] 는 우리가 찾으려는 루프 전류의 이름을 나타냄.
[ R ] 는 저항 행렬.
[R-1]은 [R] 행렬의 역수.
I1은 -0.143A로, I2는 -0.429A입니다.
I3 = I1 – I2
따라서 I3의 합산 전류는 -0.143 – (-0.429) = 0.286A로 됩니다.
이는 연관 참조에 Kirchhoffs 회로 법칙 계산한 0.286A 전류와 동일한 값입니다.
이렇게 함으로써, 메쉬 분석은 행렬의 계산을 통해 회로를 해석하고 해결할 수 있습니다.
이것은 더 효율적이고 정확한 결과를 제공하는 방법 중 하나입니다.
3. 메쉬 전류 분석의 장점 및 다른 분석과 비교
3-1) 장점
- 간결함: 메쉬 전류 분석은 각 메쉬에 대한 방정식을 설정함으로써 회로를 간결하게 분석할 수 있습니다.
이는 복잡한 회로를 보다 단순한 부분으로 분해하여 이해하는 데 도움이 됩니다. - 효율성: 메쉬 전류 분석은 전체 회로를 각 메쉬의 전류로 분해함으로써 분석의 효율성을 높입니다.
이를 통해 전체 회로의 특성을 보다 명확하게 이해할 수 있습니다. - 정확성: 올바르게 수행된 메쉬 전류 분석은 정확한 결과를 제공합니다.
이는 전기 회로의 동작을 이해하고 문제를 해결하는 데 필요한 정확한 정보를 제공합니다.
3-2) 다른 분석과 비교
- 노드 분석과의 비교
메쉬 전류 분석은 노드 분석과 대비되는데, 노드 분석은 회로의 노드에서의 전압을 중심으로 분석합니다.
반면, 메쉬 전류 분석은 각 메쉬에서의 전류를 중심으로 분석합니다.
노드 분석은 회로의 특정 부분에 더 효과적일 수 있지만, 메쉬 분석은 복잡한 회로 전체를 더 잘 이해할 수 있습니다. - 수식의 복잡성
일부 경우에는 메쉬 전류 분석의 수식이 노드 분석에 비해 더 복잡할 수 있습니다.
그러나 대부분의 경우, 메쉬 분석은 전체적으로 더 간결하고 이해하기 쉽습니다. - 적용 가능성
메쉬 전류 분석은 주로 전류 소스가 많은 회로에 적합하며, 노드 분석은 전압 소스가 많은 회로에 적합합니다.
메쉬 전류 분석은 회로 분석에 있어 중요한 방법 중 하나로, 다른 분석 기법과 함께 사용되어 전체 회로의 이해를 돕는 데 큰 역할을 합니다.
4. 주의 사항과 고려 사항
메쉬 분석을 수행할 때 주의해야 할 사항과 고려해야 할 점들이 있습니다.
- 회로의 특성에 따른 메쉬 분석의 한계
메쉬 분석은 대부분의 회로에 적용될 수 있지만, 일부 특수한 경우에는 한계가 있을 수 있습니다.
예를 들어, 회로에 비선형 요소가 포함되거나 시간에 따라 변하는 경우에는 메쉬 분석이 복잡해질 수 있습니다. - 근사치와 정확한 해의 차이에 대한 고려
메쉬 분석은 계산의 편의를 위해 근사치를 사용할 수 있습니다.
하지만 이러한 근사치는 실제 회로의 동작과 정확한 해와의 차이를 낳을 수 있습니다.
따라서 결과를 해석할 때 이러한 차이를 고려해야 합니다. - 회로의 구성 요소 해석
회로 내에 포함된 각 구성 요소의 특성을 정확하게 이해해야 합니다.
저항, 콘덴서, 인덕터 등의 요소는 메쉬 분석에 영향을 줄 수 있으며, 이를 고려하여 분석해야 합니다. - 노드와 메쉬의 적절한 설정
메쉬 분석을 수행하기 전에 적절한 노드와 메쉬를 설정해야 합니다.
잘못된 노드나 메쉬의 설정은 잘못된 결과를 가져올 수 있으므로 주의해야 합니다. - 수학적 오류 방지
계산 과정에서의 수학적 오류를 방지하기 위해 신중하게 계산해야 합니다.
실수나 부정확한 계산이 전체 결과를 왜곡할 수 있습니다.
메쉬 분석을 수행할 때 이러한 주의사항과 고려할 사항을 명심하여 신중하게 접근해야 합니다.
이를 통해 정확하고 신뢰할 수 있는 결과를 얻을 수 있습니다.
