Contents
1. RC 미분기란 무엇인가?
RC 미분기는 입력 신호의 순간적인 변화에 민감하게 반응하는 회로입니다.
즉, 입력 신호가 급격히 변할 때 이를 빠르게 감지하고 출력 신호로 반영하는 특징을 가지고 있습니다.
이 회로는 저항(Resistor, R)과 커패시터(Capacitor, C)가 직렬로 연결되어 있어, 입력 신호에 대한 변화를 미분하는 형태로 동작하게 됩니다.
이를 통해 신호의 변화를 추출해낼 수 있기 때문에 RC 미분기 동작 원리는 특히 신호 처리, 신호 감지, 펄스 신호 생성 등의 분야에서 매우 유용하게 사용됩니다.
1-1) RC 미분기의 기본 개념
RC 미분기의 기본 개념은 ‘입력 신호의 변화율에 따라 출력이 결정된다’는 것입니다.
쉽게 말해, 입력 신호가 빠르게 변하면 그 변화량을 출력 신호로 빠르게 반영하고, 느리게 변하면 출력이 거의 없거나 매우 작아집니다.
신호의 기울기를 미분하여 출력에 반영하는 형태이므로, 일종의 엣지 검출기처럼 작동한다고도 볼 수 있습니다.
낮은 주파수에서는 커패시터의 리액턴스(XC)가 높아, 직류(DC) 전압이나 천천히 변하는 신호를 차단합니다.
반면, 높은 주파수에서는 커패시터의 리액턴스가 낮아져, 빠르게 변하는 펄스 신호가 입력에서 출력으로 바로 전달됩니다.
이는 주파수에 따라 커패시터의 리액턴스(XC)와 저항(R)의 비율이 달라지기 때문입니다.
주파수가 낮을수록 출력은 줄어들고, 주어진 시간 상수에서 입력 펄스의 주파수가 높아질수록 출력 신호는 점점 더 입력 펄스와 유사한 형태로 변합니다.
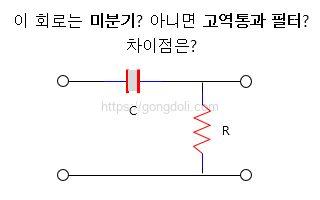
이 효과로 인해 만약 입력 신호가 사인파라면, RC 미분기는 단순한 고역통과 필터처럼 동작합니다.
이때 필터의 컷오프 주파수 또는 코너 주파수는 회로의 RC 시간 상수(τ)에 해당합니다.
따라서, 순수한 사인파를 입력으로 받을 때 RC 미분기 동작 원리에 따라 회로는 기본적인 패시브 고역통과 필터처럼 작동하며, 이때 커패시터의 리액턴스 공식인 XC = 1/(2πƒC)에 의해 결정됩니다.
결론적으로, RC 미분기 회로는 입력 신호의 미분을 수행하는 동시에 주파수에 따른 필터링을 제공하여, 고주파 신호에 대한 출력 반응이 더 크다는 특성을 가집니다.
RC 미분기 동작 원리를 바탕으로 회로의 동작을 이해하면, 신호 처리 및 필터링 응용에서의 활용성을 높일 수 있습니다.
1-2) 회로 구성 및 동작 원리
RC 미분기의 회로 구성은 매우 간단합니다.
저항(R)과 커패시터(C)가 직렬로 연결된 상태에서, 입력 신호는 이 두 요소를 통과하게 됩니다.
일반적으로 커패시터는 입력 신호와 저항 사이에 위치하며, 출력은 저항 양단에서 측정됩니다.
이때 중요한 점은 커패시터가 신호를 ‘저장’하는 성질을 가지고 있다는 것인데, 이는 신호가 변화할 때 커패시터가 그 변화에 반응하는 방식으로 나타납니다.
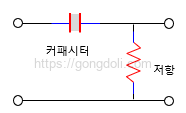
RC 미분기 동작 원리를 이해하려면, 커패시터가 충전 및 방전되는 과정을 상상해보면 됩니다.
입력 신호가 빠르게 변할 때, 커패시터는 그 변화를 즉각적으로 받아들이지 못하고 순간적으로 높은 전압을 출력하게 됩니다.
반면, 입력 신호가 천천히 변하거나 일정하면 커패시터는 거의 충전되지 않으며, 결과적으로 출력 신호도 매우 작습니다.
구체적으로 살펴보면, 입력 신호가 급격히 증가하면 커패시터는 그 변화를 즉시 따라잡지 못해 저항을 통해 출력에서 높은 전압이 발생합니다.
반대로, 입력 신호가 일정하거나 느리게 변할 때는 커패시터가 거의 반응하지 않기 때문에 출력 신호는 거의 0에 가깝습니다.
RC 미분기 동작 원리는 바로 이러한 커패시터의 성질에 기반한 것입니다.
결국, RC 미분기 동작 원리는 입력 신호의 변화를 감지하고 그 변화를 출력으로 나타내는 특성을 가진 회로라고 할 수 있습니다.
예를 들어, 직각파와 같은 급격히 변하는 신호를 입력하면, RC 미분기는 그 변화를 빠르게 반영하여 출력 신호가 급격히 변하는 패턴을 보여주게 됩니다.
- 연관 참조 : RC 충전, RC 회로 충전 시간, 충전 과정, 시간 상수, 전압.전류 변화
- 연관 참조 : RC 회로 방전 시간,전압 변화, 시간 상수, 예시1
- 연관 참조 : 적분기,RC 적분기 동작 원리, 예제1, 입력 신호에 따른 출력 변화
- 연관 참조 : RC 회로 상수 계산기, 장점 및 단점, 사용 방법
2.RC 미분기 회로 수식 설명
RC 미분기 동작 원리에서 커패시터는 입력 신호의 변화에 따라 출력 전압과 전류를 결정하는 중요한 역할을 합니다.
이를 통해 회로의 동작 원리를 더 잘 이해할 수 있으며, 특히 전압 출력과 전류 특성을 모두 다루게 됩니다.
RC 미분기 회로에서 커패시터는 저항과 직렬로 연결되어 있으며, 입력 전압 Vin(t)이 전체 회로에 인가됩니다.
출력 전압은 저항에 걸리는 전압입니다.
2-1) 커패시터 전류와 입력 전압
입력 전압 Vin(t)이 인가되면, 커패시터를 통해 흐르는 전류는 입력 전압의 변화율에 비례합니다.
이를 커패시터 전류 수식으로 표현하면
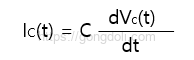
- 여기서
I𝐶(𝑡)는 시간 𝑡에서 커패시터를 통해 흐르는 전류
𝐶는 커패시턴스(커패시터의 용량)
𝑉𝐶(𝑡)는 시간 𝑡에서 커패시터에 걸리는 전압
𝑑𝑉𝐶(𝑡)/dt는 커패시터 전압의 시간에 따른 변화율을 의미
입력 전압이 빠르게 변화할수록 커패시터를 통해 흐르는 전류가 커집니다.
dt는 시간의 아주 작은 변화를 의미합니다.
이를 통해 시간에 따른 변화를 미세한 순간으로 나눠서 보는 것을 나타냅니다.
따라서 𝑑𝑡는 “시간을 잘게 쪼개서 보는” 개념이며, 이때의 변화율을 미분이라고 합니다.
이를 통해 입력 전압이 시간이 지남에 따라 어떻게 변하는지를 아주 작은 시간 단위로 살펴볼 수 있습니다.
2-2) 출력 전압 (저항에 걸리는 전압)
저항 R을 통과하는 전류는 출력 전압을 생성합니다.
옴의 법칙에 따르면
Vout(t)=iC(t)×R
여기서 커패시터 전류 수식을 대입하면,
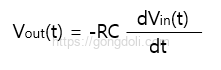
이것이 RC 미분기 수식으로, 출력 전압이 입력 전압의 변화율에 비례함을 보여줍니다.
결국, RC 미분기에서 출력 전압은 입력 전압의 변화가 얼마나 빠르게 일어나는지를 계산한 값이 됩니다.
예를 들어, 입력 전압이 빠르게 변하면 출력 전압도 큰 값을 가지게 되고, 입력 전압이 천천히 변하면 출력 전압은 작은 값을 가집니다.
2-3) 주파수에 따른 동작
고주파 신호: 입력 신호가 빠르게 변화(고주파수)할 때는 커패시터가 빠르게 충전 및 방전하므로 출력 전압이 급격히 변합니다.
저주파 신호: 입력 신호가 느리게 변화(저주파수)할 때는 커패시터를 통해 흐르는 전류가 작아져 출력 전압도 작게 나타납니다.
이때 회로는 저주파 성분을 차단하는 고역 통과 필터처럼 작동할 수 있습니다.
RC 미분기 회로에서는 출력 전압이 입력 전압의 변화율에 비례하며, 커패시터를 통한 전류는 입력 전압의 시간에 따른 변화에 비례합니다.
회로의 시간 상수 τ=RC는 입력 신호 변화에 대한 회로의 반응 속도를 결정하며, 고주파 신호에서는 출력이 입력 신호를 더 밀접하게 따르고, 저주파 신호는 필터링되어 출력 전압이 줄어듭니다.
커패시터 전류와 출력 전압 특성을 모두 이해함으로써 RC 미분기 회로가 다양한 입력 신호에 어떻게 반응하는지 알 수 있으며, 주파수에 따라 고역 통과 필터나 신호 미분 장치로 작동할 수 있습니다.
3. RC 미분 회로 동작 원리
RC 미분기 동작 원리를 이해하려면 먼저, 단일 펄스가 입력으로 들어왔을 때 회로가 어떻게 반응하는지 살펴볼 필요가 있습니다.
단일 전압 스텝 펄스가 RC 미분기 회로에 처음 입력되면, 커패시터는 빠르게 변화하는 신호에 대해 초기에는 단락 회로처럼 동작합니다.
왜냐하면, 사각파의 상승 가장자리에서 전압의 변화율 𝑑𝑉/𝑑𝑡이 매우 크기 때문입니다(이론적으로는 무한대).
이 순간에는 모든 입력 전압이 출력으로 전달되어 저항에 걸리는 전압으로 나타납니다.

입력 신호가 일정한 값을 유지하는 동안, 커패시터는 정상적인 방식으로 저항을 통해 충전되기 시작합니다.
충전 속도는 RC 타임 상수, 즉τ=RC에 의해 결정됩니다.
커패시터가 충전됨에 따라 저항에 걸리는 전압, 즉 출력 전압은 지수 함수적으로 감소하여, 커패시터가 완전히 충전되면 출력 전압이 0이 됩니다.
이 시점에서 커패시터에 걸리는 전압𝑉𝐶는 입력 펄스의 전압과 같아집니다.
VC=Vin
만약 입력 펄스가 다시 0으로 돌아가면, 𝑑𝑉/𝑑𝑡이 매우 큰 음의 변화가 발생합니다.
이때 커패시터는 급격한 전압 변화를 감지할 수 없으므로 출력에서 음의 스파이크가 발생합니다.
이후 커패시터는 정상적으로 방전되며 출력 전압은 다시 지수 함수적으로 증가하기 시작합니다.
따라서 RC 미분기 동작 원리에 따르면, 입력 신호가 급격히 변할 때마다 출력에서 전압 스파이크가 발생합니다.
입력 신호가 양의 방향으로 변화하면 양의 스파이크가, 음의 방향으로 변화하면 음의 스파이크가 출력됩니다.
이 결과, RC 미분기 출력은 입력 신호의 변화율을 반영한 그래프가 되며, 입력 신호가 사각파일지라도 출력은 사각파와 전혀 다른 형태의 양의 스파이크와 음의 스파이크로 구성됩니다.
입력 펄스의 주기 𝑇를 조정하면 RC 미분기 동작 원리에 따라 출력 펄스의 모양도 변화하며, 이는 입력 신호와 RC 타임 상수 사이의 관계에 의해 결정됩니다.
4.RC 미분기 시간 상수에 따른 출력 파형
RC 미분기 회로에서 출력 파형의 모양은 펄스 폭과 RC 시간 상수의 비율에 따라 달라집니다.
RC 시간 상수가 펄스 폭보다 훨씬 크면(예: 10RC 이상), 출력 파형은 입력 신호의 스퀘어 파형과 유사한 모양을 가지게 됩니다.
반면, RC 시간 상수가 펄스 폭보다 훨씬 작으면(예: 0.1RC 이하), 출력 파형은 매우 가파르고 좁은 피크 형태를 가지게 됩니다.
즉, RC 시간 상수를 변경하면 다양한 출력 파형을 얻을 수 있습니다.
일반적으로 RC 미분기 회로에서는 작은 시간 상수를 사용하는 것이 보편적입니다.
이렇게 하면 저항 𝑅에 걸리는 출력에서 날카롭고 뚜렷한 펄스를 얻을 수 있습니다.
예를 들어, 스퀘어 파형 펄스의 미분 결과(높은𝑑𝑉/𝑑𝑡 를 가진 스텝 입력)는 극히 짧은 스파이크 형태로 나타납니다.
이것이 RC 미분기 회로의 동작 원리입니다.

4-1) 예시
스퀘어 파형의 주기가 T=20ms이고, 펄스 폭이 10ms(주기의 절반)라고 가정해 보겠습니다.
이때 출력 전압이 초기 값의 37%까지 감소하려면 펄스 폭이 RC 시간 상수와 같아야 합니다.
즉, RC=10ms입니다.
만약 커패시터의 값 C를 1μF로 설정하면, 저항 R의 값은 10kΩ이 됩니다.
출력이 입력과 유사한 모양을 가지게 하려면, RC 시간 상수는 펄스 폭의 10배인
10RC여야 합니다.
따라서 같은 커패시터 값 1μF일 때, 저항 R은 100kΩ이어야 합니다.
반면 출력이 날카로운 펄스 형태를 가지려면 RC 시간 상수가 펄스 폭의 1/10인 0.1RC여야 하며, 이 경우 저항 R은 1kΩ이 됩니다.
즉, RC 미분기 동작 원리에서 가장 중요한 점은 입력 신호의 변화율, 즉 dV/dt에 따라 출력 신호의 모양이 달라진다는 것입니다.
입력 신호가 일정할 때는 출력이 0이지만, 입력이 급격히 변화하면 출력에서 날카로운 전압 피크가 발생합니다.
또한, RC 시간 상수가 클수록 출력 파형은 입력 신호에 가까워지고, 시간 상수가 작을수록 출력은 더 짧고 뚜렷한 펄스 형태를 나타냅니다.
5.RC 미분기의 입력 파형에 따른 출력 특성
RC 미분기는 입력 신호의 변화율에 따라 출력이 달라지며, 입력 신호가 급격히 변할수록 출력도 크게 반응합니다.
이는 RC 미분기의 핵심적인 특성으로, 신호가 얼마나 빠르게 변하는지를 포착해 출력에 반영하는 역할을 합니다.
RC 미분기 동작 원리를 이해하기 위해서는 입력 신호에 따라 출력이 어떻게 달라지는지를 살펴보는 것이 중요합니다.
5-1) 입력 신호에 따른 출력 변화
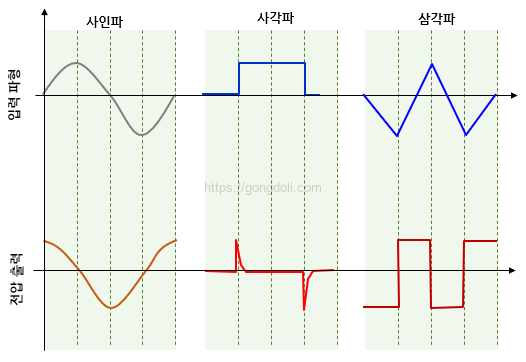
RC 미분기 동작 원리에서 가장 흥미로운 부분은 입력 신호의 형태에 따라 출력이 어떻게 변하는지입니다.
- 사각파 입력 : 사각파는 순간적으로 전압이 급격히 상승하거나 하강하는 특성을 가지고 있습니다.
이런 신호를 RC 미분기에 입력하면, 전압이 급격히 상승하는 순간에는 출력에서 큰 긍정적인 스파이크가 발생하고, 전압이 급격히 떨어지는 순간에는 큰 음의 스파이크가 발생합니다.
그 이유는, RC 미분기 동작 원리에서 중요한 것은 신호의 변화율이기 때문입니다.
사각파는 신호의 변화율이 매우 크기 때문에 그에 상응하는 출력 변화가 큰 것입니다. - 삼각파 입력 : 삼각파는 선형적으로 증가하고 감소하는 신호로, 사각파와 달리 신호가 부드럽게 변합니다.
이러한 입력이 RC 미분기에 입력되면, 출력 신호는 일정한 값으로 출력되다가, 기울기가 바뀌는 순간에 출력이 반대 방향으로 변화합니다.
삼각파의 기울기(즉, 변화율)가 일정하기 때문에, 출력 신호는 일정한 값으로 나타나는 것입니다. - 사인파 입력 : 사인파는 매끄럽게 변하는 신호로, RC 미분기에서는 신호의 기울기(미분 값)가 출력됩니다.
사인파가 최고점에서 기울기가 0이 되는 순간, 출력은 0에 가깝게 됩니다.
반대로, 사인파가 빠르게 증가하거나 감소하는 순간, 출력은 그에 맞춰 최대 또는 최소 값을 가집니다.
이는 RC 미분기 동작 원리에서 신호의 변화율이 중요한 요소로 작용하기 때문입니다.
이처럼 입력 신호의 형태에 따라 RC 미분기 동작 원리는 다르게 작동하며, 입력 신호가 얼마나 빠르게 변하는지에 따라 출력 신호의 크기와 형태가 달라집니다.

Very interesting information!Perfect just what I was searching for! “I have a hundred times wished that one could resign life as an officer resigns a commission.” by Robert Burns.
Thank you for your kind feedback!
Appreciate it for all your efforts that you have put in this. very interesting info .
Thank you so much for your kind words! It’s truly rewarding to know that the information provided resonates with you.
Nice post. I was checking continuously this blog and I’m impressed! Extremely useful info particularly the last part 🙂 I care for such info much. I was seeking this certain information for a very long time. Thank you and good luck.
Thank you so much for your kind words
I am not real wonderful with English but I find this real easygoing to read .
Thank you so much for your kind words!
I’m really glad you found the content easy to read.
I’m not very fluent in English either
I simply could not depart your website before suggesting that I extremely loved the standard info an individual provide to your visitors? Is gonna be again ceaselessly in order to inspect new posts.
That means a lot—thank you for such kind words!
I just couldn’t go away your website before suggesting that I really enjoyed the usual information an individual provide in your guests? Is going to be back regularly in order to check out new posts
Thanks so much—hope to see you back soon!
I like what you guys are up also. Such intelligent work and reporting! Keep up the excellent works guys I have incorporated you guys to my blogroll. I think it’ll improve the value of my site :).
Thank you so much—I’m honored to be part of your blogroll!
I was curious if you ever thought of changing the structure of your site? Its very well written; I love what youve got to say. But maybe you could a little more in the way of content so people could connect with it better. Youve got an awful lot of text for only having one or 2 images. Maybe you could space it out better?
Thank you for your thoughtful feedback. I’ll keep your suggestions in mind to improve the layout and balance.
I’m still learning from you, but I’m trying to achieve my goals. I definitely liked reading everything that is written on your website.Keep the stories coming. I loved it!
Thank you so much! I’m glad you enjoyed the posts and I’ll keep sharing more.
Great blog here! Also your web site loads up fast! What host are you using? Can I get your affiliate link to your host? I wish my website loaded up as quickly as yours lol
Thank you! I’m glad you find the blog excellent and the site fast. I use a Korean hosting service, so I don’t have an affiliate link to share, but I appreciate your interest.
Very nice post. I just stumbled upon your blog and wanted to say that I have truly enjoyed browsing your blog posts. In any case I will be subscribing to your feed and I hope you write again very soon!
Thank you for your kind words. I’m glad you enjoyed the posts and subscribed to the feed.