Contents
1. 밀만의 정리 개념
밀만의 정리(Millman’s theorem)는 전기 회로 분석에서 사용되는 중요한 정리 중 하나입니다.
이 정리는 복수의 병렬 전압 source가 있는 회로에서 전압을 쉽게 계산하는 데 사용됩니다.
밀만의 정리는 여러 개의 병렬 전압 source가 있는 회로에서 전압을 계산하는 방법을 제공합니다.
이 정리는 모든 병렬 전압 source의 전압에 해당하는 가중 평균을 사용하여 전체 회로의 전압을 계산합니다.
Millman’s theorem는 병렬 연결된 전압 source가 있는 회로에 적용됩니다.
병렬로 연결된 전압 source가 있을 때 이를 단일 전압으로 대체하는 데 사용됩니다.
이 정리는 병렬 연결된 전압 source의 특성을 이해하고 전압을 쉽게 계산하는 데 유용합니다.
따라서, 밀만의 정리는 병렬로 연결된 전압 source가 있는 회로에서 전압을 효과적으로 계산하는 데 사용되며, 전기 회로 분석에서 중요한 도구로 인정됩니다.
- 연관 참조 : 키르히호프의 회로 법칙, KCL, KVL, 예제, KCL vs. KVL,적용과 한계
- 연관 참조 : 메쉬 전류 분석,Mesh Current Analysis,예제, 장점 3가지, 다른 분석과 비교
- 연관 참조 : 노드 전압 분석, 분석 방법 5단계, 예제, 메쉬 전류 분석과 비교
- 연관 참조 : 노턴의 등가 회로, 정의, 분석 6단계, 예제, 한계와 주의 사항
- 연관 참조 : 테브난의 정리, 5단계 방법, 예제, 한계와 주의 사항
- 연관 참조 : 와이 델타 변환,Y-Δ 변환과 Δ-Y 변환, 변환 방정식, 예제 3개,활용
2. 밀만의 등가 회로
밀만의 정리는 여러 개의 전압 source가 병렬로 연결된 회로에서 등가 회로를 쉽게 얻는 간단한 방법을 제시합니다.
많은 회로들이 여러 개의 전압 source를 가지고 있습니다.
예를 들어, 비상 조명용 배터리 뱅크, 병렬 발전기 등이 있습니다.
이러한 병렬로 연결된 각 전압 source는 서로 다른 내부 저항(각 소스의 고유 저항)을 가지고 있으며, 전체 소스 집합은 부하(RL)에 연결됩니다.
회로의 다이어그램을 확인해보면(이미지의 왼쪽 부분을 참조), 각 각의 Source가 병렬로 연결되어 있음을 알 수 있습니다.
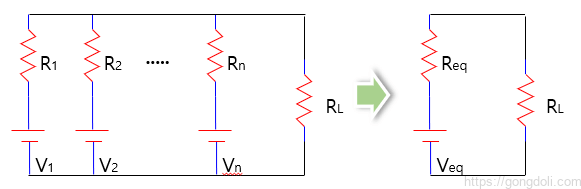
밀만의 정리를 사용하면 등가 회로를 얻을 수 있습니다(다이어그램의 오른쪽 부분 참조).
Millman’s theorem를 사용하기 위해서는 회로를 병렬 분기로 재구성해야 합니다(가능한 경우),
각 분기는 전압 source와 직렬 저항(임피던스)으로 구성되거나 전류 source와 병렬 저항(임피던스)으로 구성됩니다.
여기서,
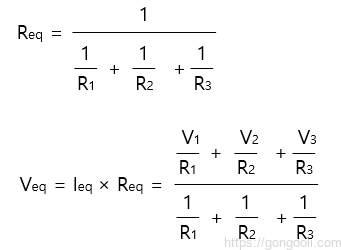
이와 같은 방식으로 Millman’s theorem를 사용하여 병렬로 연결된 여러 전압 source를 가진 회로의 등가 회로를 쉽게 얻을 수 있습니다.
3. 예제 풀이
부하 저항의 등가 회로를 찾고, 부하에 공급되는 전류를 찾는 것은 전기 회로 분석에서 중요한 단계입니다.
이를 위해서는 밀만의 정리를 이용해서 풀어보겠습니다.
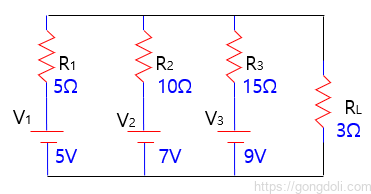

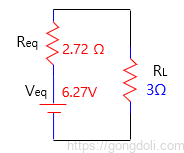
즉, 부하에 공급되는 전류는
IL = V / (Req + RL) = 6.27 V / 5.72 Ω = 1.09 A
4. 오옴의 법칙 vs 키르히호프의 법칙 vs 밀만의 정리 비교
| 특성 | 오옴의 법칙 | 키르히호프의 법칙 | 밀만의 정리 |
|---|---|---|---|
| 적용 대상 | 단일 회로 내의 전압, 전류, 저항 | 여러 회로 요소를 포함한 복잡한 회로 분석 | 병렬로 연결된 여러 전압 소스에 대한 등가 회로 분석 |
| 기본 원리 | 전류는 저항에 비례하며, 저항은 전압에 비례한다 | 회로 내의 전압 또는 전류에 대한 등식을 세워 전체 회로를 해석 | 병렬로 연결된 전압 소스의 등가 회로를 찾아 쉽게 회로를 해석하는 방법 |
| 사용 목적 | 회로 내의 특정 부분에 대한 전압, 전류, 저항을 계산 | 복잡한 회로의 전압 및 전류를 계산하여 회로 동작을 이해 | 병렬로 연결된 여러 전압 소스에 대한 등가 회로를 찾아 회로를 간단하게 해석 |
| 적용 가능성 | 단일 회로 내에서 전압, 전류, 저항에 대한 계산 | 복잡한 회로에 적용되며, 여러 노드 및 요소가 있는 회로를 해석 가능 | 병렬로 연결된 여러 전압 소스가 있는 회로에서만 적용 가능한 방법 |
| 회로 해석 난이도 | 단순한 회로에서 쉽게 적용 가능 | 회로의 복잡성에 따라 해석이 어려울 수 있음 | 병렬로 연결된 회로에서만 사용 가능하며, 이 경우 쉽게 회로를 해석할 수 있음 |
5. 밀만의 정리 한계와 주의 사항
5-1) 밀만의 정리가 적용되지 않는 경우
- Millman’s theorem는 병렬로 연결된 여러 전압 소스에 대한 등가 회로를 찾는 것에만 적용됩니다.
- 만약 회로가 복잡하게 연결되어 있거나, 다른 회로 구성 요소가 포함되어 있다면, 밀만의 정리를 적용할 수 없을 수 있습니다.
5-2) 밀만의 정리의 한계와 근거리
- Millman’s theorem는 오직 병렬로 연결된 여러 전압 source에만 적용됩니다.
- 회로에 시간에 따라 변하는 요소(주파수 응답 등)가 포함되어 있는 경우, 정확한 등가 회로를 찾는 것이 어려울 수 있습니다.
5-3) 밀만의 정리의 정확성과 신뢰성에 대한 주의사항
- 밀만의 정리는 가정과 근사치에 의존합니다. 실제 회로에서는 이상적인 조건이 아닐 수 있습니다.
- 내부 저항이나 전압 소스의 변화에 따라 정확한 결과를 얻기 어려울 수 있습니다.
- 따라서, 실제 회로에서는 Millman’s theorem의 결과를 확인하기 위해 다른 방법으로 회로를 분석하는 것이 좋습니다.
즉, 밀만의 정리는 특정한 조건에서만 적용 가능하며, 실제 회로에서는 다양한 제약 사항이 존재할 수 있습니다.
Millman’s theorem를 사용할 때에는 회로의 복잡성과 정확성을 고려하여 다른 분석 방법과 함께 사용하는 것이 중요합니다.
