Contents
1. 버터워스 필터의 개요
버터워스 필터는 주파수 응답이 통과대역에서 가능한 한 평평한 특성을 가지도록 설계된 신호 처리 필터의 한 유형입니다.
버터워스 필터는 주파수 응답이 통과대역에서 가능한 한 평평한 특성을 가지도록 설계된 필터로, 이로 인해 “최대평평성 필터(maximally flat magnitude filter)”로도 불립니다.
이러한 특성은 필터를 특정 주파수 영역에서 신호를 최대한 왜곡 없이 전달하도록 만듭니다.
버터워스 필터는 1930년에 영국의 기술자이자 물리학자인 스티븐 버터워스(Stephen Butterworth)의 논문인 “필터 증폭기 이론(On the Theory of Filter Amplifiers)”에서 이 필터의 개념과 설계 방법에 대해 상세히 설명되었습니다.
버터워스 필터의 주파수 응답은 통과대역(즉, 허용 주파수 범위)에서는 평평하게 유지되며, 중지대역(즉, 차단 주파수 범위)에서는 서서히 약해지거나 감쇄됩니다.
이 감쇄 속도는 필터의 차수에 따라 다르며, 필터 회로에서 사용되는 반응 요소의 수에 따라 결정됩니다.
일반적으로 필터는 인덕터(선포)와 캐패시터(용량)를 반응 요소로 사용합니다.
그러나 버터워스 필터는 캐패시터만 사용하여 설계되기 때문에 필터의 차수는 사용된 캐패시터의 수로 결정됩니다.
버터워스 필터는 다른 필터와 비교하여 설계하기 간단하며, 특히 설계에서 고려해야 할 매개 변수가 적습니다.
이러한 간편성으로 인해 버터워스 필터는 다양한 응용 분야에서 널리 사용되고 있습니다.
음향 및 음성 처리, 통신 시스템, 바이오의학적 신호 처리 등 다양한 분야에서 사용되며, 특히 통신 시스템에서는 채널 특성을 보정하거나 원하는 대역폭을 설정하는 데 사용됩니다.
- 연관 참조 : 능동 저역 통과 필터,1차 LPF, 전압 이득, 예제1
- 연관 참조 : 능동 고역 통과 필터,이상적인 HPF, 전압 이득, 주파수 응답
- 연관 참조 : 능동 대역 통과 필터,동작 원리,회로, 반전 BPF, 예제1
2. 버터워스 필터란?
버터워스 필터는 아날로그 필터 설계 중에서 주파수 응답이 최대한 평평한 특성을 가지도록 고안된 필터입니다.
이것은 패스 밴드와 스톱 밴드에서의 리플이 없는 최대평평한 필터 응답을 제공합니다.
다시 말해, 특정 주파수 영역에서 신호를 최대한 왜곡 없이 전달하도록 만들어진 것입니다.
이러한 디자인은 특히 통신 및 제어 시스템과 같은 응용에서 중요하며, 신호의 주파수 스펙트럼을 모양있게 조절하는 데 사용됩니다.
예를 들어, 휴대전화 통신 시스템에서는 송신된 신호의 주파수를 정확하게 제어하여 통신 채널에서의 성능을 최적화해야 합니다.
이를 위해 통신 시스템에서는 여러 필터가 사용되며, 그 중에서도 버터워스 필터는 주파수 응답이 가능한 한 평평하여 데이터 전송 속도와 품질을 최대한 유지하는 데 효과적입니다.
버터워스 필터의 특징 중 하나는 그 평평한 주파수 응답과는 대조적으로 비교적 넓은 트랜지션 밴드(transition band)를 가진다는 것입니다.
트랜지션 밴드는 패스 밴드와 스톱 밴드 사이의 주파수 범위를 나타내며, 필터의 주파수 특성이 패스 밴드에서 스톱 밴드로 원활하게 전환되는 곳입니다.
이러한 특징은 필터의 차수와 관련이 있습니다.
필터의 차수는 필터 회로 내에 사용된 반응성 요소의 수에 의해 결정됩니다.
버터워스 필터에서는 주로 캐패시터만을 사용하며, 따라서 필터의 차수는 사용된 캐패시터의 수에 의해 결정됩니다.
일반적으로, 필터의 차수가 높을수록 트랜지션 밴드의 너비가 좁아지고 롤오프 속도가 빨라집니다.
예를 들어, 1차 필터의 경우 표준 롤오프 속도는 20dB/decade(6dB/octave)입니다.
그러나 2차 필터의 경우 롤오프 속도가 40dB/decade(12dB/octave)로 두 배가 됩니다.
이와 같은 방식으로 3차, 4차, 5차 등의 고차 필터는 더 빠른 롤오프 속도를 제공합니다.
고차 필터를 구성할 때는 일반적으로 단일 필터를 연결하여 형성합니다.
예를 들어, 2차 저역 통과 필터 두 개를 연결하여 4차 저역 통과 필터를 만들 수 있습니다.
그러나 필터의 차수가 증가함에 따라 필터의 크기와 비용이 증가하고, 정확도가 감소할 수 있습니다.
따라서 필터를 설계할 때는 주파수 응답의 평평함과 트랜지션 밴드의 너비, 필터의 차수와 그에 따른 롤오프 속도 등을 고려해야 합니다.
이를 통해 원하는 응용에 가장 적합한 필터를 선택할 수 있습니다.
3. 버터워스 필터 주파수 응답
3-1) Decades and Octaves
버터워스 필터에서 “decades”와 “octaves”는 주파수 응답의 롤오프 속도를 설명하는 중요한 개념입니다.
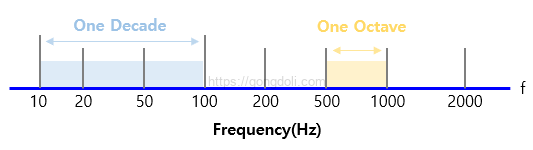
3-1-1) Decades(데케이드)
데케이드는 주파수 스케일에서 10배의 차이를 의미합니다. 즉, 한 데케이드는 주파수 영역에서 10배의 너비를 나타냅니다.
따라서, 필터의 주파수 응답이 데케이드 단위로 롤오프할 때는 해당 주파수에서 출력 신호의 에너지가 10배(또는 1/10배)로 감소합니다.
3-1-2) Octaves(옥타브)
옥타브는 주파수 스케일에서 2배의 차이를 의미합니다. 즉, 한 옥타브는 주파수 영역에서 2배의 너비를 나타냅니다.
필터의 주파수 응답이 옥타브 단위로 롤오프할 때는 해당 주파수에서 출력 신호의 에너지가 2배(또는 1/2배)로 감소합니다.
버터워스 필터에서는 주로 데케이드 단위로 롤오프 속도를 설명합니다.
일반적으로 1차 필터의 경우, 주파수가 한 데케이드씩 증가할 때 출력 신호의 에너지가 20dB씩 감소합니다.
즉, 1차 필터의 롤오프 속도는 20dB/decade입니다.
따라서, 2차 필터의 경우 롤오프 속도는 40dB/decade, 3차 필터의 경우는 60dB/decade, 그리고 4차 필터의 경우는 80dB/decade로 증가합니다.
이와 같은 방식으로 필터의 차수가 증가할수록 롤오프 속도도 증가하게 됩니다.
이러한 데케이드와 옥타브의 개념을 이해하면 필터의 주파수 응답이 어떻게 변화하는지 이해하는 데 도움이 됩니다.
특히 주파수 스펙트럼에서의 필터의 동작을 이해하는 데 중요합니다.
3-2) 로그 주파수 스케일
버터워스 필터에서 로그 주파수 스케일은 필터의 주파수 응답을 분석하고 설명하는 데 사용되는 중요한 도구입니다.
로그 주파수 스케일은 주파수를 일정한 간격으로 표현하는 대신, 로그 함수에 따라 스케일이 조정됩니다.
이러한 스케일링은 주파수 스펙트럼에서의 신호의 변화를 더 잘 이해할 수 있도록 도와줍니다.
특히 주파수 스펙트럼은 일반적으로 로그 스케일로 표시되어 있으며, 이는 인간의 청각 시스템이 주파수에 로그 스케일을 사용하여 음성과 음악을 인식하기 때문에 자연스러운 선택입니다.
로그 주파수 스케일에서는 각 주파수 간의 간격이 일정하지 않습니다.
대신 주파수 간의 간격이 더 넓은 범위에서 일어납니다.
예를 들어, 100Hz에서 200Hz로 이동하는 것은 2000Hz에서 4000Hz로 이동하는 것과 동일한 주파수 비율을 나타냅니다.
전자 회로에서는 로그 주파수 척도가 특히 유용합니다.
왜냐하면 이 척도를 사용하면 관련된 넓은 주파수 범위를 더 쉽게 시각화하고 분석할 수 있기 때문입니다.
특히 버터워스 필터와 같이 주파수 결정 저항과 커패시터가 동일한 경우에는 주파수가 결정되는 컷오프 또는 코너 주파수 (ƒ𝐶)가 필터 차수(첫 번째, 두 번째, 세 번째 또는 네 번째)와 상관없이 동일하게 유지됩니다.
컷오프 주파수는 이제 우리가 잘 알고 있는 공식을 사용하여 찾을 수 있습니다.
ƒC = 1/ 2πRC
이 공식은 컷오프 주파수와 저항 및 커패시터의 곱의 역 관계를 강조합니다.
RC의 곱이 증가하면 컷오프 주파수가 감소하여 낮은 주파수로 이동함을 나타내며,
RC가 감소하면 컷오프 주파수가 증가하여 더 높은 주파수로 이동함을 나타냅니다.
로그 주파수 척도를 사용하고 필터 회로의 구성 요소와 컷오프 주파수 간의 관계를 이해함으로써, 엔지니어들은 필터를 보다 효과적으로 설계하고 분석하여 원하는 주파수 응답과 성능 특성을 보장할 수 있습니다.
4. 버터워스 필터의 근사화(Approximation)
버터워스 필터의 근사화(Approximation)는 실제 필터 응답과 이론적인 이상적인 응답 간의 차이를 설명합니다.
이 필터는 이상적인 최대평평한 특성을 가지므로, 이상적인 필터와의 차이가 더 크게 나타나는 경우가 많습니다.
이 차이를 이해하고 관리하기 위해 다양한 근사화 기법이 사용됩니다.
- 오차 함수(Approximation Error Function)
오차 함수는 실제 필터 응답과 이상적인 응답 간의 차이를 설명하는 함수입니다.
이 함수는 주로 주파수 응답에서의 차이를 나타내며, 필터의 주파수 특성을 분석하는 데 사용됩니다. - 근사화 유형(Approximation Types)
버터워스 필터에서 사용되는 주요 근사화 유형에는 버터워스 근사화, 바이텍 근사화, 치비셰프 근사화 등이 있습니다.
각각의 근사화 방법은 필터의 주파수 응답을 근사화하는 방식에 따라 다릅니다. - 주파수 응답 특성(Frequency Response Characteristics)
필터 근사화는 주파수 응답 특성에 직접적인 영향을 미칩니다.
이상적인 버터워스 필터의 경우, 주파수 응답은 패스 밴드에서 완전히 평평하며, 스톱 밴드에서는 완전한 롤오프를 보입니다.
그러나 근사화된 필터는 이 이상적인 특성을 보장하지 않을 수 있습니다. - 오버슈팅(Overshoot) 및 언더슈팅(Undershoot)
근사화된 필터는 종종 오버슈팅 및 언더슈팅 현상을 보일 수 있습니다.
이는 필터의 주파수 응답이 이상적인 경우보다 더 크게 나타나는 현상을 나타냅니다. - 차수(Ordern)
필터의 차수가 높을수록 근사화가 더 정확하게 이루어집니다.
따라서 높은 차수의 필터를 사용하면 더 낮은 근사화 오차를 얻을 수 있습니다.
버터워스 필터의 근사화는 이상적인 필터와의 차이를 최소화하고 원하는 주파수 응답 특성을 달성하기 위해 중요합니다.
따라서 실제 응용에서는 근사화 오차를 최소화하기 위해 적절한 필터 차수와 근사화 유형을 선택하는 것이 중요합니다.
5. 1차 로우패스 버터워스 필터
5-1) 회로
버터워스 필터에서 필요한 통과 대역 이득은 주로 ‘R1’과 ‘Rf’의 저항 값에 따라 결정되며, 필터의 차단 주파수는 회로에 사용된 저항과 콘덴서의 값에 따라 달라집니다.
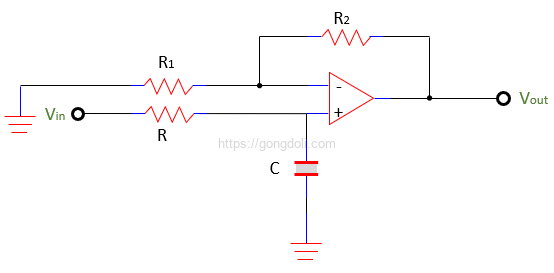
간단히 말해서, 필터의 이득은 ‘R1’과 ‘Rf’의 비율에 의해 설정됩니다.
‘R1’과 ‘Rf’의 비율이 높을수록 필터의 이득이 커지고, 낮을수록 이득이 줄어듭니다.
이는 필터가 신호를 얼마나 증폭시킬지를 결정합니다.
차단 주파수는 주로 회로에 사용된 저항과 콘덴서의 값에 따라 결정됩니다.
이 값들이 커지면 차단 주파수가 낮아지고, 작아지면 차단 주파수가 높아집니다.
따라서 회로에 사용되는 구성 요소의 선택은 필터의 작동 특성을 결정하는 데 중요한 역할을 합니다.
5-2) 동작
패스밴드 이득: 버터워스 필터의 패스밴드 이득은 주로 저항 R1과 Rf의 비율에 의해 결정됩니다.
이는 패스밴드 주파수 범위 내에서 필터의 이득을 설정합니다.
컷오프 주파수: 컷오프 주파수(fc)는 패스밴드에서 스톱밴드로의 전환을 결정하는 중요한 매개 변수입니다.
이것은 저항 R 및 커패시터 C의 값에 의해 결정되며, 𝑓𝑐=1/2𝜋𝑅𝐶로 주어집니다.
전달 함수: 필터의 전달 함수는 주파수 응답을 설명합니다.
극좌표 형식에서는
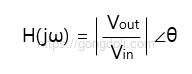
로 표현되며, 여기서 ω는 각주파수입니다.
크기 응답은
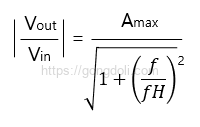
로 주어지며,
위상 응답은
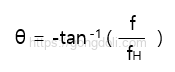
여기서 𝑓𝐻는 -3dB 주파수 또는 half-power 주파수입니다.
5-3) 특성
- 패스밴드 및 스톱밴드: 패스밴드에서는 저주파 신호가 통과하고, 스톱밴드에서는 고주파 신호가 차단됩니다.
- 이득: 저주파에서는 패스밴드 이득이 일정하며, 고주파에서는 감소합니다.
이런 특성은 주파수가 컷오프 주파수에 가까워질수록 나타납니다. - 롤오프 비율: 이 필터의 롤오프 비율은 20dB/decade 또는 6dB/octave입니다.
이는 주파수가 컷오프 주파수를 넘어갈수록 이득이 감소하는 비율을 나타냅니다.
6. 버터워스 필터의 이상적인 주파수 응답
아래 그래프는 버터워스 필터의 이상적인 주파수 응답을 보여줍니다.
그래프의 x축은 주파수를 나타내고, y축은 이득을 나타냅니다.
이 그래프를 통해 버터워스 필터의 주요 특징을 이해할 수 있습니다.
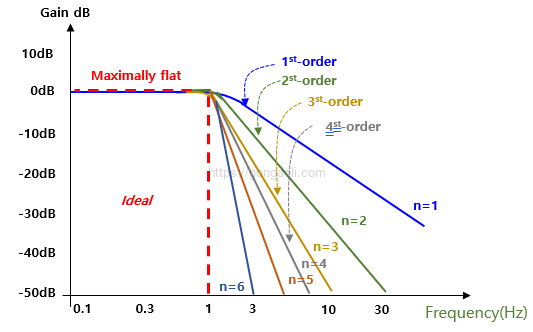
6-1) 패스밴드의 최대평평성(Maximally Flat Passband)
그래프의 왼쪽 부분에서 주파수가 낮은 영역은 패스밴드를 나타냅니다.
이 영역에서 필터는 최대한 평평한 응답을 보여야 합니다.
즉, 가능한 한 주파수가 일정하게 통과되도록 해야 합니다.
이 그래프에서는 주파수가 패스밴드에 있는 경우에는 이득이 거의 변하지 않고 일정한 값을 유지하는 것을 볼 수 있습니다.
6-2) 스톱밴드의 롤오프(Roll-off in the Stopband)
그래프의 오른쪽 부분에서 주파수가 높아지면 스톱밴드에 접어들게 됩니다.
스톱밴드에서는 필터가 신호를 차단하고, 이 때 필터의 이득이 점차적으로 감소해야 합니다.
이 그래프에서는 주파수가 스톱밴드에 가까워질수록 이득이 부드럽게 감소하는 것을 볼 수 있습니다.
6-3) 컷오프 주파수(Cutoff Frequency)
그래프에서 이득이 -3dB 지점에 도달하는 지점은 컷오프 주파수입니다.
이 지점은 패스밴드와 스톱밴드 사이의 경계를 나타내며, 이 지점 이상의 주파수에서는 필터가 점점 더 많은 신호를 차단하게 됩니다.
6-4) 리플(Ripple)
그래프에서는 이상적인 버터워스 필터이기 때문에 리플이나 왜곡이 없는 것으로 나타납니다.
즉, 그래프가 평평하게 유지되며 어떠한 주파수에서도 이득의 변동이 없는 것을 볼 수 있습니다.
이러한 그래프를 통해 버터워스 필터가 원하는 대로 작동하는지를 시각적으로 확인할 수 있으며, 필터의 주요 특성을 이해하는 데 도움이 됩니다.
6-5) 차수
버터워스 필터의 차수는 필터의 주파수 응답 특성에 중요한 영향을 미칩니다.
차수가 높을수록 필터의 롤오프 특성이 더 가파르게 변화하므로, 주파수 응답이 더 빠르게 변화합니다.
1차 필터
1차 필터는 가장 낮은 차수의 필터로, 주파수 응답의 변화가 가장 완만합니다.
그래프에서 1차 필터는 컷오프 주파수 근처에서 이득이 -3dB로 감소하기 시작하며, 이론적으로 20dB/decade의 롤오프 비율을 갖습니다.
따라서 1차 필터의 주파수 응답은 비교적 완만한 편입니다.
2차 필터
2차 필터는 1차 필터보다 더 빠르게 롤오프가 발생합니다.
그래프에서 2차 필터는 컷오프 주파수 근처에서 이득이 더 빠르게 감소하는 것을 볼 수 있습니다. 이론적으로 40dB/decade의 롤오프 비율을 갖습니다.
따라서 2차 필터는 주파수 응답의 변화가 더 빠릅니다.
3차 필터
3차 필터는 2차 필터보다 더 가파른 롤오프를 갖습니다.
그래프에서 3차 필터는 컷오프 주파수 근처에서 더 급격한 이득 감소를 보여줍니다.
이론적으로 60dB/decade의 롤오프 비율을 갖습니다.
따라서 3차 필터는 주파수 응답의 변화가 더 빠르며, 스톱밴드에서 더 급격한 감쇠를 제공합니다.
이렇게 차수가 높아질수록 필터의 주파수 응답이 더 빠르게 변화하고, 롤오프 특성이 더 가파르게 됩니다.
따라서 차수가 필터의 동작 특성을 결정하는 중요한 요소 중 하나입니다.
7. 저역 통과 버터워스 필터의 다항식
버터워스 필터의 정규화된 저역 통과 버터워스 필터 다항식은 필터의 주파수 응답을 설명하는 데 사용됩니다.
이러한 다항식은 주파수 응답을 특정 형식으로 표현하여 필터의 특성을 분석하는 데 도움이 됩니다.
다음은 버터워스 필터의 정규화된 저역 통과 버터워스 필터 다항식의 일반적인 형태입니다.
- 여기서
- Hn(s)는 n차 버터워스 필터의 전달 함수입니다.
- 𝑠는 라플라스 변환 도메인의 변수입니다.
- ωc는 정규화된 컷오프 주파수입니다.
- 이는 컷오프 주파수를 임계 주파수로 나누어 구합니다.
- 𝜔𝑐=2𝜋𝑓𝑐/𝑓𝑠 여기서 fc는 실제 컷오프 주파수이고, fs는 샘플링 주파수입니다.
- 𝑛n은 필터의 차수입니다.
이러한 다항식은 주파수 응답을 모델링하는 데 사용될 수 있으며, 필터 설계 및 분석에 중요한 도구입니다.
이러한 다항식을 사용하여 필터의 주파수 응답을 계산하고, 컷오프 주파수와 필터 차수를 조정하여 원하는 필터 특성을 얻을 수 있습니다.
아래는 버터워스 필터의 정규화된 2차 저역 통과 다항식을 나타내는 표입니다.
각 차수에 해당하는 다항식은 주어진 공식을 따라 계산됩니다.
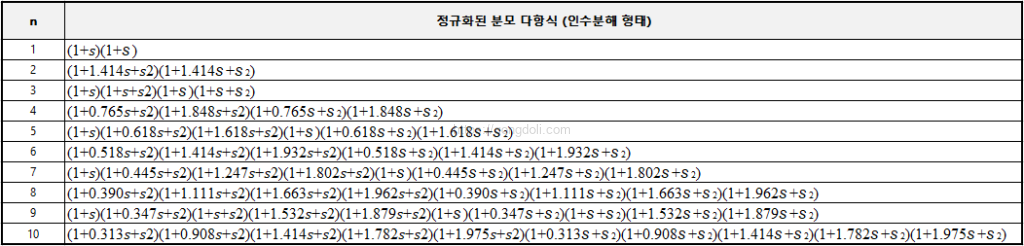
이러한 다항식은 버터워스 필터의 설계와 분석에 사용될 수 있으며, 필터의 주파수 응답을 모델링하는 데 도움이 됩니다.