병렬 인덕터, 정의, 공식, 예제 3개

1. 개요

병렬 인덕터는 회로의 전체 인덕턴스를 증가시키는 데 사용됩니다.
이들은 서로 다른 두 인덕터가 병렬로 연결되어 전류가 흐르는 방향에 따라 각 인덕터의 자기장이 서로 상쇄되지 않도록 설계됩니다.

병렬 인덕터를 사용하면 회로의 전체 인덕턴스를 증가시킬 수 있습니다.
이는 회로에 대한 전기적 특성을 조절하는 데 유용합니다.
예를 들어, 고주파 회로에서는 병렬 인덕터가 회로의 공명 주파수를 조절하고 필요한 에너지 저장을 제어하는 데 사용될 수 있습니다.

이러한 병렬 인덕터는 또한 전원 공급 안정성을 향상시키고 회로의 스파이크와 노이즈를 줄이는 데도 도움이 됩니다.
따라서 병렬 인덕터는 다양한 전기 및 전자 회로에서 중요한 구성 요소로 사용됩니다.
예를 들어, 스위칭 전원 공급기, 필터 회로, 고주파 변환기 및 레이더 시스템에서 병렬 인덕터가 널리 사용됩니다.

이러한 병렬 인덕터는 일반적으로 자기 간섭을 최소화하기 위해 서로 다른 방향으로 배치되거나 물리적으로 격리되어 설계됩니다.
이렇게 함으로써 인덕터 간의 상호 작용을 최소화하고 원하는 전기적 특성을 달성할 수 있습니다.

종종 병렬 인덕터는 다른 전기 구성 요소와 함께 사용되어 전원 공급 안정성을 향상시키고 회로의 성능을 최적화하는 데 기여합니다. 이러한 이유로 병렬 인덕터는 다양한 전자 및 전기 공학 응용 분야에서 중요한 역할을 합니다.

• 연관 참조 : 인덕터 특성, 코어의 종류, 구조와 동작원리, 특성 4가지,선택 주의 사항
• 연관 참조 : 코일의 인덕턴스,예제 2개, 선택 고려 사항
• 연관 참조 : 나선형 코일 인덕턴스 계산기,Helical coil inductance calculator, 사용 방법
• 연관 참조 : 상호 인덕턴스, 원리, 결합 계수, 예제 2개,자기 인덕턴스와 비교
• 연관 참조 : 유도 리액턴스,정의,위상 다이어그램, 주요 문제 및 해결책 4가지
• 연관 참조 : 직렬 인덕터,정의, 예제, 병렬 분류,분류에 따른 예제 2개
• 연관 참조 : 플레밍의 왼손 법칙과 오른손 법칙, 이해, 차이점
• 연관 참조 : 패러데이 전자기 유도,패러데이 실험, 1법칙, 2법칙, 차이점, 중요성
• 연관 참조 : 렌츠의 법칙, 동작 원리, 패러데이 법칙과 차이

2. 병렬 인덕터란?

병렬 연결된 인덕터의 경우, 각 인덕터는 독립적으로 작동하며 병렬 회로를 형성합니다.
이러한 인덕터는 각각 독립적으로 작동하므로 병렬 연결된 인덕터의 등가 인덕턴스를 계산할 때는 직렬 연결과는 달리 다른 방법을 사용해야 합니다.

2-1) 병렬로 연결된 인덕터

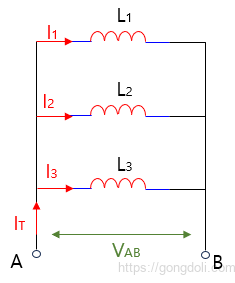
먼저 병렬로 연결된 인덕터의 등가 회로 인덕턴스 LT를 계산하려면 각 인덕터를 흐르는 전류의 합인 총 전류 I_T를 구해야 합니다.
이를 위해 Kirchhoff의 전류 법칙을 사용하여 병렬 회로에 있는 모든 인덕터에 흐르는 전류의 합이 총 전류 I_T가 됩니다.

그리고 각 인덕터에 걸리는 전압은 인덕터의 자기 유도에 의해 발생하는데, 이는 인덕터의 변화하는 전류에 의해 발생하는 자기 유도 전압입니다.

따라서 병렬 연결된 인덕터 회로에서는 각 인덕터의 전류를 고려하여 총 전류에 대한 등가 전압을 구하고, 이를 통해 병렬 회로의 등가 인덕턴스를 계산할 수 있습니다.

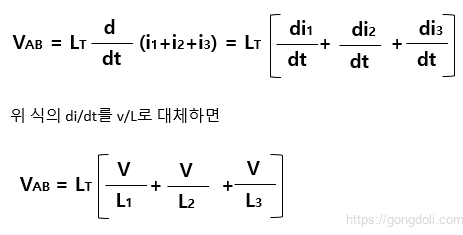
우리는 이것을 간추려서 병렬 회로의 총 인덕턴스를 계산하는 최종 식으로 줄일 수 있습니다.

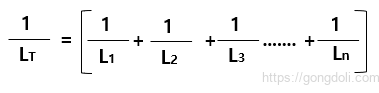
이것은 병렬 연결의 총 인덕턴스의 역수가 모든 인덕터의 개별 인덕턴스의 역수의 합이라는 것을 의미합니다.
위의 식은 병렬 연결된 코일 사이에 상호 인덕턴스가 없을 때 영향을 받습니다.

분수를 다룰 때 복잡함을 피하기 위해 우리는 총 인덕턴스를 계산하기 위해 곱셈 방법을 사용할 수 있습니다.
두 개의 인덕터가 병렬로 연결되어 있고, 그들 사이에 상호 인덕턴스가 없다면, 총 인덕턴스는 다음과 같이 주어집니다

L_T = (L₁× L₂)/(L₁+ L₂)

2-2) 예제

회로에 20 Henry와 30 Henry의 2개의 인덕터가 병렬로 연결되어 있다면 병렬 배열의 총 인덕턴스는 얼마인지 계산해 보겠습니다.

전체 인덕턴스 계산 공식은

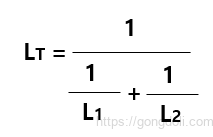
주어진 인덕턴스가 각각 20H 와 30H인 경우

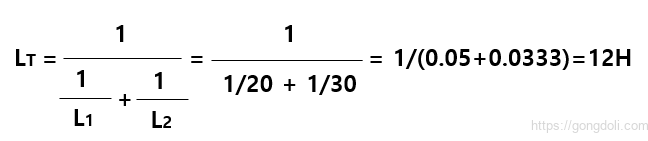
따라서 병렬 배열의 전체 인덕턴스는 대략 12 H입니다.

3. 병렬 인덕터(Mutually Coupled )

3-1) 병렬 방식의 상호 결합 인덕터

병렬로 연결된 인덕터는 서로의 자기장을 링크하게 되어 상호 인덕턴스의 효과가 발생합니다.
이 효과는 각 코일 사이의 자기 결합 정도에 따라 전체 인덕턴스를 증가시키거나 감소시킵니다.
이러한 상호 인덕턴스의 영향은 코일 간의 간격과 서로의 방향에 따라 달라집니다.

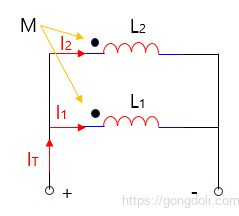
병렬로 연결된 상호 연결된 인덕터는 전체 인덕턴스를 “보조(aiding)”하거나 “반대(opposing,역방향)”하는 두 가지 방식으로 분류됩니다.
보조 연결된 병렬 코일은 전체 동등 인덕턴스를 증가시키고, 반대로 연결된 코일은 전체 동등 인덕턴스를 감소시킵니다.
이는 상호 인덕턴스가 없는 코일과 비교하여 나타납니다.

상호 결합된 병렬 코일은 극성 점 또는 극성 표시를 사용하여 서로의 상태를 나타낼 수 있습니다.
이것은 각 코일의 자기장이 어떻게 상호 작용하는지를 나타내며, 전체 인덕턴스의 변화에 영향을 줍니다.

3-2) 병렬 보조(Aiding) 인덕터

위의 설명에서 두 인덕터가 병렬로 연결되어 있기 때문에, 두 인덕터 사이의 전압은 동일해야 합니다.
따라서 두 인덕터를 통과하는 전류 i1과 i2는 전압 유지를 위해 조절됩니다.
이로 인해 두 병렬 보조 인덕터의 총 인덕턴스 LT는 다음과 같이 표시됩니다.

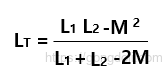
• 여기서
• 2M은 코일 L₁이 L₂에 미치는 영향을 나타냄
• 코일 L₂도 L₁에 미치는 영향을 나타냄

만약 두 인덕터의 인덕턴스가 서로 동일하고, 상호 인덕턴스가 완벽하게 형성된 경우(예: 도선 회로), 두 인덕터의 등가 인덕턴스는 L_T = L₁ = L₂ = M이 됩니다.
그러나 두 인덕터 사이에 상호 인덕턴스가 없는 경우, 등가 인덕턴스는 두 개의 자기 유도 인덕터의 경우와 마찬가지로 L ÷ 2가 됩니다.

만약 두 인덕터 중 하나의 극성이 반대라면, 두 병렬 인덕터는 상대적으로 연결되어 있고, 그 결과 상호 인덕턴스 M은 각 인덕터의 효과를 상쇄시킵니다.

3-3) 병렬 반대(Opposing,역방향) 인덕터

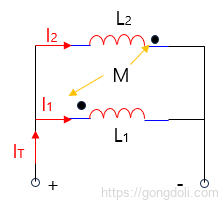
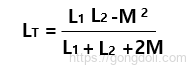
두 인덕터가 서로 동일한 값을 갖고 있고, 이들 사이에 완벽한 자기 결합이 있다면, 등가 인덕턴스와 인덕터를 통한 자기 유도 전압은 모두 0이 됩니다.
이것은 두 인덕터가 서로 상쇄되기 때문입니다.

두 인덕터에 순차적으로 흐르는 전류 i1과 i2는 서로 반대 방향인 두 인덕터 간에 발생하는 총 상호 플럭스가 0이 되므로, 두 인덕터가 서로 상쇄됩니다.
따라서 두 인덕터는 회로에서 전류의 흐름을 단락으로 만들어지게 되고, 등가 인덕턴스 LT는 (L ± M) ÷ 2와 같이 계산됩니다.

이것은 인덕터가 서로 상쇄되기 때문에 새로운 전류 경로가 형성되고, 결과적으로 전압이 인덕터를 통해 더 이상 발생하지 않게 되는 것을 의미합니다.
이러한 상황에서는 인덕터가 회로에서 “쇼트” 상태가 되어 전류의 흐름을 막게 됩니다.

3-4) 예제 1

자기 인덕턴스가 각각 75mH와 55mH인 두 개의 인덕터를 병렬로 연결합니다. 상호 인덕턴스는 22.5mH입니다.
이때 전체 인덕턴스를 계산해보겠습니다.

인덕터의 공식은

L_T=(L₁​+L₂​+2M)

• 여기서
• L_T은 병렬 조합의 총 인덕턴스
• L_1​ 과 L₂는 두 인덕터의 자기 인덕턴스
• M은 두 인덕터 사이의 상호 인덕턴스

문제에서 주어진 값은

• L₁​=75 mH
• L_2​=55 mH
• M=22.5 mH

주어진 값을 공식에 대입하면

L_T=(L₁​+L₂​+2M) = (75mH+55mH+2×22.5mH) = 175mH

따라서, 두 개의 인덕터가 병렬로 연결되어 있고, 상호 인덕턴스가 22.5mH인 경우, 총 인덕턴스는 175mH입니다.

3-5) 예제 2

다음 유도 회로의 등가 인덕턴스를 계산해 보겠습니다.

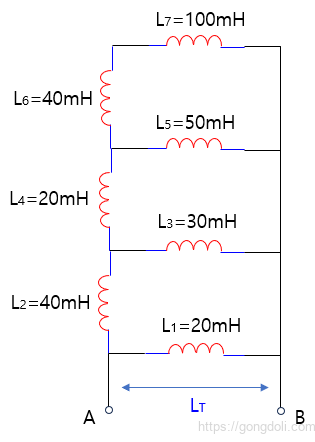
첫 번째 인덕터 분기 L_A를 계산합니다(인덕터 L₆ 및 L₇과 병행하는 인덕터 L₅)

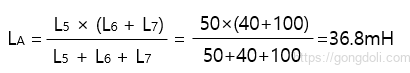
두 번째 인덕터 분기 L_B, (인덕터 L₄ 및 L_A와 병행하여 인덕터 L₃)를 계산합니다

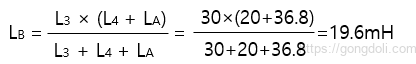
마지막으로 등가 회로 인덕턴스 L_T, (인덕터 L₂ 및 L_B와 병렬로 인덕터 L1)를 계산합니다

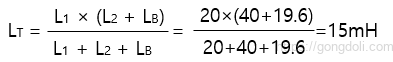
따라서, 위 회로의 등가 인덕턴스는 15mH입니다.