부동소수점과 고정소수점 변환,변환이 필요?,변환하는 방법,예시2

Contents

1. 부동소수점과 고정소수점이란?
2. 왜 부동소수점과 고정소수점 변환이 필요한가?
3. 부동소수점에서 고정소수점으로 변환하는 방법
4. 고정소수점에서 부동소수점으로 변환하는 방법

1. 부동소수점과 고정소수점이란?

부동소수점과 고정소수점 변환이 필요할 때, 이 두 표현 방식의 차이를 이해하는 것이 중요합니다.
왜냐하면, 각각의 시스템 요구 사항에 따라 적합한 표현 방식을 선택함으로써 성능과 정확성을 최적화할 수 있기 때문입니다.
예를 들어, 정밀도가 중요한 경우 부동소수점이 더 적합할 수 있으며, 반대로 속도와 메모리가 중요한 경우 고정소수점이 더 나은 선택이 될 수 있습니다.

1-1) 부동소수점(Floating Point)의 정의

부동소수점은 컴퓨터 과학에서 숫자를 표현하는 한 방법으로, 매우 큰 수와 매우 작은 수를 표현하는 데 적합합니다.
간단히 말해, 부동소수점은 소수점을 “떠다니게” 하여 다양한 크기의 숫자를 표현할 수 있게 합니다.
이를 위해 부동소수점은 아래와 같은 형식을 사용합니다.

Number=Sign×Mantissa×Base^Exponent

Sign (부호): 숫자가 양수인지 음수인지 나타냅니다.
Mantissa (가수): 숫자의 유효 자릿수를 나타냅니다.
Base (기수): 일반적으로 2입니다. 즉, 이진수 체계를 사용합니다.
Exponent (지수): 가수를 몇 번 곱할지 또는 나눌지 결정합니다.

부동소수점 표현을 사용하면 매우 큰 수(예: 3.4 × 10³⁸)와 매우 작은 수(예: 1.2 × 10^-38)를 효율적으로 표현할 수 있습니다.
이 때문에 과학 계산, 그래픽 처리 등 다양한 분야에서 부동소수점이 널리 사용됩니다.

부동소수점과 고정소수점 변환이 중요한 이유는 주로 이런 다양한 숫자 표현 방식이 서로 다른 장단점을 가지기 때문입니다.
부동소수점은 높은 정밀도와 넓은 범위의 숫자를 다룰 수 있지만, 계산 속도가 느릴 수 있으며, 소수점 이하 자릿수에 대한 정밀도 손실이 발생할 수 있습니다.

1-2) 고정소수점(Fixed Point)의 정의

고정소수점은 부동소수점과 달리 소수점의 위치가 고정되어 있는 숫자 표현 방식입니다.
즉, 숫자의 전체 자릿수 중 몇 자리를 소수점 이하에 할당할지를 미리 정해놓는 것입니다.
예를 들어, 8자리의 숫자 중에서 소수점 이하에 2자리를 할당한다면, 1234.56처럼 표현할 수 있습니다.

고정소수점의 장점
간단하고 빠른 연산: 정수 연산과 유사하기 때문에 계산이 매우 빠릅니다.
정확한 소수점 제어: 특정 자리의 소수점 이하를 정밀하게 다룰 수 있습니다.

고정소수점은 특히 임베디드 시스템이나 디지털 신호 처리(DSP)와 같은 하드웨어 제약이 있는 환경에서 자주 사용됩니다.
이런 시스템에서는 부동소수점의 높은 정밀도보다 연산 속도와 메모리 사용 효율이 더 중요한 경우가 많기 때문입니다.

부동소수점과 고정소수점 변환이 필요할 때, 고정소수점 방식은 부동소수점보다 단순하며, 예측 가능한 숫자 범위를 제공하므로, 실시간 처리 요구 사항이 있는 시스템에서 더욱 선호됩니다.

1-3) 두 가지 표현 방식의 차이점

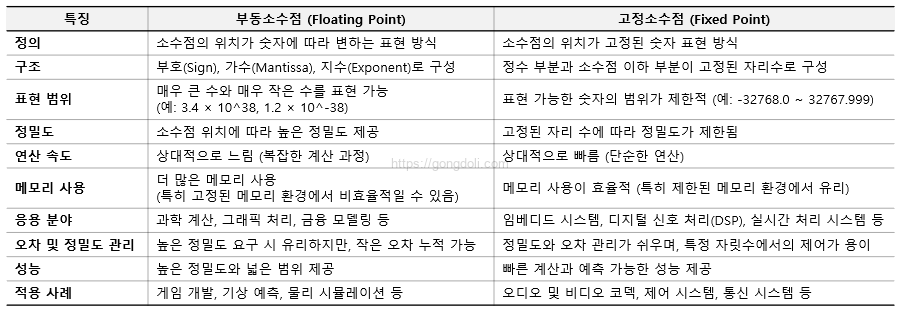
각 방식은 다양한 응용 분야에서 특정한 장단점을 가지고 있으며, 부동소수점과 고정소수점 변환이 필요한 경우 각 방식의 특성을 고려하여 선택하는 것이 중요합니다.

연관 참조 : 비트와 바이트 차이점, 발전 과정, 차이점 3가지, 중요성
연관 참조 : 2의 보수와 부호화,계산 방법,활용,부호화 개념,부호화 장점
연관 참조 : 이진수(Binary) 란?, 표기, 구조, 이진수 변환, 덧셈, 뺄셈, 곱셈, 나눗셈 연산, 예제, 컴퓨터
연관 참조 : 8진수_octal, 십진수 & 2진수로 변환, 8진수 연산,예제
연관 참조 : 16진수 (hexadecimal),표기법과 구조,16진수↔10진수/2진수 변환 예제,16진수연산

2. 왜 부동소수점과 고정소수점 변환이 필요한가?

부동소수점과 고정소수점은 각기 다른 방식으로 숫자를 표현하는 방법입니다.
그렇다면 왜 우리는 이 두 가지 표현 방식 간의 변환이 필요할까요?
다양한 이유가 있지만, 성능과 메모리 최적화, 정밀도와 정확성 요구 사항, 그리고 특정한 응용 분야의 특성 때문에 부동소수점과 고정소수점 변환이 필요합니다.

2-1) 성능 및 메모리 최적화

부동소수점과 고정소수점 변환은 성능과 메모리 최적화에 매우 중요합니다.
특히 제한된 리소스를 가진 시스템에서는 효율적인 메모리 사용과 빠른 계산이 필수적입니다.

부동소수점은 복잡한 수학 연산을 수행하는 데 유리하지만, 계산 속도가 느릴 수 있습니다.
이는 복잡한 수식에서 높은 정밀도가 요구될 때 필요한 경우가 많습니다.
예를 들어, 기상 시뮬레이션이나 물리 시뮬레이션에서 부동소수점을 사용하면 정확한 결과를 얻을 수 있습니다.
반면, 고정소수점은 간단한 수학 연산에서 빠른 성능을 제공하며, 특히 하드웨어에서 매우 효율적으로 작동합니다.
예를 들어, 임베디드 시스템에서 센서 데이터를 처리할 때, 고정소수점을 사용하면 연산 속도가 훨씬 빨라지고 메모리 사용이 줄어듭니다.
이 시스템에서는 고정소수점의 정해진 자릿수로 인해 예측 가능한 성능을 유지할 수 있습니다.

따라서, 성능이 중요한 시스템에서는 부동소수점과 고정소수점 변환을 통해 빠르고 효율적인 연산을 구현할 수 있습니다.
신호 처리 시스템에서는 부동소수점을 사용하여 데이터를 정밀하게 분석한 후, 고정소수점으로 변환하여 빠르게 처리할 수 있습니다.

2-2) 정밀도 및 정확성 요구 사항

부동소수점과 고정소수점 변환은 정밀도와 정확성 요구 사항을 충족시키는 데에도 중요합니다.
각 표현 방식은 특정한 수준의 정밀도와 정확성을 제공하며, 이 요구 사항은 응용 프로그램에 따라 다릅니다.

부동소수점은 매우 높은 정밀도를 제공할 수 있어, 매우 작은 변화도 표현할 수 있습니다.
예를 들어, 과학 연구나 금융 모델링에서 매우 정밀한 계산이 필요할 때 부동소수점이 사용됩니다.
이는 부동소수점이 소수점 위치를 자유롭게 조정할 수 있기 때문에 가능합니다.
반면, 고정소수점은 정밀도가 제한적이지만, 특정 자릿수에서의 정확한 제어가 가능하여 특정 응용에서 매우 유용합니다.
예를 들어, 오디오 및 비디오 코덱에서는 고정소수점을 사용하여 데이터 압축과 해제를 신속하게 수행하면서도, 적절한 수준의 정밀도를 유지할 수 있습니다.

정밀도와 정확성이 중요한 시스템에서는 부동소수점과 고정소수점 변환을 통해 적절한 표현 방식을 선택할 수 있습니다.
예를 들어, 디지털 신호 처리(DSP)에서는 신호를 정확하게 분석하기 위해 부동소수점을 사용하고, 분석 결과를 고정소수점으로 변환하여 빠르게 처리할 수 있습니다.

2-3) 적용 분야 예시: 임베디드 시스템, DSP

부동소수점과 고정소수점 변환은 특히 임베디드 시스템과 디지털 신호 처리(DSP) 분야에서 중요한 역할을 합니다.
이들 분야에서는 각 표현 방식의 특성을 잘 활용해야만 시스템의 효율성을 극대화할 수 있습니다.

임베디드 시스템: 이러한 시스템은 종종 제한된 메모리와 처리 능력을 가지고 있으며, 실시간으로 작동해야 하는 경우가 많습니다.
예를 들어, 마이크로컨트롤러 기반의 임베디드 시스템에서는 센서 데이터 처리나 제어 작업에 고정소수점을 사용하여 메모리 사용을 최소화하고, 빠른 연산을 가능하게 합니다.
그러나, 데이터 수집 및 초기 분석 단계에서는 부동소수점을 사용하여 높은 정밀도를 유지할 수 있습니다.
이런 시스템에서 부동소수점과 고정소수점 변환은 데이터 처리의 효율성과 정확성을 보장하는 데 필수적입니다.
디지털 신호 처리(DSP): DSP 시스템은 오디오, 비디오 및 통신 신호를 처리할 때 자주 사용됩니다.
여기서는 신호의 분석 및 변환에 높은 정밀도가 필요하지만, 실시간 처리를 위해 빠른 연산이 중요합니다.
예를 들어, 오디오 신호의 주파수 분석에는 부동소수점이 필요할 수 있지만, 그 신호를 출력 장치로 전송하거나 실시간 처리를 위해서는 고정소수점이 더 적합할 수 있습니다.
따라서, DSP 시스템에서 부동소수점과 고정소수점 변환은 성능과 정밀도 간의 균형을 맞추는 데 필수적입니다.

이와 같이, 부동소수점과 고정소수점 변환은 다양한 분야에서 중요한 역할을 하며, 각 응용 분야의 특성에 맞추어 적절하게 사용될 때 시스템의 성능과 효율성을 최적화할 수 있습니다.
부동소수점과 고정소수점 변환의 중요성을 이해하고 이를 적절히 활용하는 것은 현대의 컴퓨팅 환경에서 매우 중요합니다.

3. 부동소수점에서 고정소수점으로 변환하는 방법

부동소수점과 고정소수점 변환은 수학적 연산, 데이터 처리 및 저장 효율성을 위해 필수적입니다.
여기서는 부동소수점 수를 고정소수점 수로 변환하는 과정을 이해하기 쉽게 설명해 보겠습니다.

3-1) 부동소수점 수의 구조

부동소수점 수는 크게 세 부분으로 구성됩니다.(위에서 설명)

부호(Sign), 지수(Exponent), 가수(Mantissa).

부호 (Sign): 숫자가 양수인지 음수인지 나타내는 1비트입니다.
지수 (Exponent): 가수를 몇 번 기수(Base)로 곱할지 나타내는 부분입니다.
일반적으로 지수는 편향된 값(biased value)으로 저장됩니다.
예를 들어, IEEE 754 표준에서 단정밀도 부동소수점의 지수는 127을 기준으로 편향됩니다.
가수 (Mantissa): 실제 숫자의 유효 숫자 부분으로, 1보다 크거나 같은 수로 정규화됩니다.

예를 들어, IEEE 754 표준의 단정밀도 부동소수점은 다음과 같이 구성됩니다.

부호: 1비트
지수: 8비트
가수: 23비트

이러한 구조를 통해 매우 큰 수와 매우 작은 수를 표현할 수 있으며, 이로 인해 부동소수점 수는 다양한 수학적 연산에서 사용됩니다.

3-2) 고정소수점 수의 구조

고정소수점 수는 정수와 유사한 방식으로, 소수점이 고정된 위치에 있는 숫자 표현 방식입니다.
이는 숫자를 정수 부분과 소수 부분으로 나누는 방식으로 정의됩니다.
고정소수점 수는 주로 다음과 같이 구성됩니다.

정수 부분: 소수점 위의 자리수들로, 숫자의 전체 크기를 결정합니다.
소수 부분: 소수점 이하의 자리수들로, 숫자의 정밀도를 결정합니다.

고정소수점은 시스템에 따라 다르게 구성될 수 있지만, 일반적으로 n비트의 정수 부분과 m비트의 소수 부분으로 나뉩니다.
예를 들어, 16비트 고정소수점 표현에서는 상위 8비트가 정수 부분, 하위 8비트가 소수 부분일 수 있습니다.

이러한 구조는 계산이 매우 간단하고 빠르며, 메모리 사용이 효율적입니다.
이는 임베디드 시스템과 같은 메모리 제약이 있는 환경에서 특히 유용합니다.

10진수->부동소수점 변환 계산기

3-3) 변환 절차와 계산 예제

부동소수점에서 고정소수점으로 변환하는 과정은 다음과 같습니다.

부동소수점 수의 분리: 부동소수점 수를 부호, 지수, 가수로 분리합니다.
실수로 변환: 부호, 지수, 가수를 사용하여 부동소수점 수를 실수 형태로 변환합니다.
스케일링: 실수 형태의 숫자를 고정소수점에서 표현할 수 있는 범위로 스케일링합니다.
이를 위해 고정소수점의 스케일 팩터를 결정합니다.
정수 변환: 스케일된 실수를 정수로 변환하여 고정소수점으로 표현합니다.

예를 들어, IEEE 754 표준을 사용하여 부동소수점 수 1.75를 16비트 고정소수점으로 변환한다고 가정해 보겠습니다.
여기서 고정소수점은 8비트의 정수 부분과 8비트의 소수 부분으로 구성됩니다.

a) 부동소수점 분리

부호: 0 (양수)
지수: 127 + 0 = 127
가수: 1.75 → 1.75 = 1.11000000000000000000000 (2진수)

b) 실수로 변환

1.75=1×2⁰×(1+0.75)=1.75

c) 스케일링

고정소수점의 정수 부분과 소수 부분이 8비트씩이므로, 스케일 팩터는 2⁸=256입니다.
1.75×256=448

d) 정수 변환

스케일된 실수 448을 16비트로 표현하면, 16비트 고정소수점 수는 448=0000000111000000(2진수)입니다.

3-4) C/C++ 코드 예시

다음은 C/C++에서 부동소수점 수를 고정소수점 수로 변환하는 예제 코드입니다.

이 코드는 부동소수점 값 $1.75$ 를 고정소수점으로 변환합니다.
여기서 fractionalBits는 고정소수점에서 소수점 이하 자릿수를 나타냅니다.
이 예제에서는 소수점 이하 8비트를 사용하므로 스케일 팩터는 $256$ 입니다.

4. 고정소수점에서 부동소수점으로 변환하는 방법

고정소수점에서 부동소수점으로 변환하는 과정은 부동소수점에서 고정소수점으로 변환하는 과정과 반대입니다.
이 과정에서는 고정된 위치의 소수점을 부동소수점 표현으로 변환하여 더 큰 범위와 정밀도를 얻습니다.

4-1) 고정소수점 수에서 부동소수점 수로의 변환 과정

고정소수점 수를 부동소수점으로 변환하는 과정은 다음과 같습니다.

스케일링 백: 고정소수점 수를 원래 실수 형태로 복원하기 위해 스케일 팩터를 사용하여 값을 조정합니다.
부동소수점 표현: 복원된 실수를 부동소수점 형식으로 변환합니다.
이를 위해 소수점 위치를 조정하고, 부호, 지수, 가수를 계산합니다.

예를 들어, 16비트 고정소수점 수 448을 부동소수점 수로 변환한다고 가정해 보겠습니다.
여기서 고정소수점은 8비트의 정수 부분과 8비트의 소수 부분으로 구성됩니다.

a) 스케일링 백

고정소수점 수 448를 스케일 팩터 2⁸=256으로 나눕니다.
448/256=1.75

b) 부동소수점 표현

1.75는 부호: 0 (양수), 지수: 127 + 0 = 127, 가수: 1.75 (1.11000000000000000000000)
따라서, 부동소수점 표현은 IEEE 754 표준에 따라 1.75입니다.

4-2) 계산 방법과 예제

고정소수점 수를 부동소수점 수로 변환하는 계산 방법을 예로 들어 설명하겠습니다.

예를 들어, 고정소수점 수가 256 (8비트 정수, 8비트 소수)라고 가정해 보겠습니다.