1. 부동소수점 변환 계산기?
부동소수점 변환 계산기는 사용자가 10진수와 부동소수점을 서로 변환할 수 있는 웹 기반 계산기입니다.
이 도구는 단정밀도(32비트)와 배정밀도(64비트)를 선택할 수 있어 다양한 데이터 타입의 변환을 지원합니다.
1-1) 계산기 특징 및 장.단점
사용자는 변환 종류(10진수 → 부동소수점 또는 부동소수점 → 10진수)와 변환할 숫자를 선택하고, 비트 너비(32비트 또는 64비트)를 설정할 수 있습니다.
계산 결과는 부호, 지수, 가수로 분리되어 상세하게 표시되어 변환 과정을 이해하는 데 도움이 됩니다.
초기화 버튼을 통해 입력값을 쉽게 초기화할 수 있어 사용이 편리합니다.
- 연관 참조 : 2진수 사칙 연산 계산기, Binary calculator, 사용 방법
- 연관 참조 : 16진수 사칙 연산 계산기, hexadecimal calculator, 사용 방법
- 연관 참조 : 8진수 사칙 연산 계산기, Hexadecimal calculator, 사용 방법
- 연관 참조 : 2진수 변환기, 8진수,16진수,십진수 변환, 사용 방법
부동소수점 표현은 컴퓨터에서 수를 저장하는 중요한 방식 중 하나입니다.
이 방법은 수를 부호(±), 지수(n), 그리고 가수(xxxxx)로 나누어 표현합니다.
수의 부호는 맨 처음 비트로 0과 1을 사용하여 나타내며, 이어서 가수 부분은 1.xxxxx 형태의 이진수로 표현됩니다.
지수는 2의 거듭제곱으로 곱해지는 수를 나타내며, 이 모든 정보를 조합하여 수를 정확하게 표현할 수 있습니다.
컴퓨터는 이 정보를 0과 1로 이루어진 이진수로 저장하며, 다시 10진수로 변환할 때에는 이 정보를 해석하여 계산을 수행합니다.
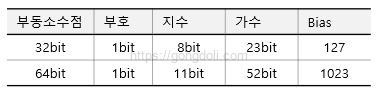
부동소수점은 특정한 규칙에 따라 표현되며, 주로 32비트와 64비트 두 가지 형식이 있습니다.
32비트의 경우 지수는 8비트로 표현되며, 이 때의 Bias 값은 127입니다.
Bias 값은 지수의 범위를 절반으로 나누어 부호와 가수를 포함하는 모든 범위를 다룰 수 있게 합니다.
반면 64비트의 경우 지수는 11비트로 표현되며, Bias 값은 1023입니다.
이를 통해 더 넓은 범위의 수를 다룰 수 있습니다.
또한, 부동소수점 표현에서는 특별한 값들이 정해져 있습니다.
범위 초과시 “반올림”
IEEE754 표기시 가수(소수점 아래부분) 표기가능 범위(예: 32bit에서는 23)를 초과하는 경우 반올림합니다.
10진수에서 5이상을 반올림 하듯, 2진수에서는 1이상을 반올림하면 됩니다.
- 0.1을 32bit 부동소수점으로 변환과정에서 가수값을 보면 반올림의 의미가 이해되실겁니다.
- 가수값: 1001100110011001100110011001… 에서
- 가수값: 10011001100110011001101 반올림된 값
- 0.1을 2진수로 바꾸면 소수점 아래부분은 1001이 반복되는데, 단정밀도(32bit)의 가수범위는 23자리까지 표현 가능하므로, 소수점 아래 24번째 자리에서 반올림하여 표현합니다.
부동소수점 변환 계산기(IEEE754)
2. 부동소수점 변환 계산기 사용 방법
사용 방법
변환할 숫자를 입력하고, 변환 종류와 비트 너비를 선택합니다.
“변환” 버튼을 클릭하여 결과를 확인합니다.
결과는 부호, 지수, 가수로 나누어져서 출력되며, 필요한 경우 10진수로의 변환 과정도 제공됩니다.
계산 결과는 계산기 하단에 표시되며, 필요한 경우 결과를 복사하여 다른 곳에 붙여넣을 수 있습니다.
주의 사항
입력하는 숫자는 올바른 형식의 10진수여야 합니다.
부동소수점 숫자의 경우 소수점 이하 자릿수를 포함하여 정확히 입력해야 정확한 변환이 이루어집니다.
변환할 비트 너비를 잘 선택해야 합니다.
단정밀도는 32비트이며, 배정밀도는 64비트이며, 이는 변환할 데이터의 정밀도에 맞게 선택해야 합니다.
계산 결과가 부동소수점의 특성과 IEEE 754 표준에 따라 반올림될 수 있습니다.
이 점을 이해하고 사용하시기 바랍니다.
