1. 부울 대수란 무엇인가?

부울 대수 법칙은 논리적 사고를 수학적으로 표현하는 방법입니다.
이는 조지 불(George Boole)이라는 영국 수학자에 의해 19세기 중반에 개발되었으며, 그의 이름을 따서 “부울 대수”라고 불립니다.
부울 대수는 0과 1이라는 두 가지 상태를 사용하여 논리 연산을 수행하며, 이를 통해 논리적 명제를 수학적으로 다룰 수 있게 합니다.

1-1) 부울 대수의 기본 개념과 역사

부울 대수 법칙의 기본 개념은 간단히 말해서, 논리 연산을 수학적으로 표현하는 체계입니다.
이는 주로 세 가지 기본 연산으로 구성됩니다.
AND(논리곱), OR(논리합), NOT(부정). 각각의 연산은 특정한 규칙에 따라 0과 1, 즉 참(True)과 거짓(False) 상태를 다룹니다.

• AND 연산 : 두 개의 입력 값이 모두 1일 때만 결과가 1이 됩니다.
  이를 기호로 표현하면 A AND B = A * B입니다.
• OR 연산 : 두 개의 입력 값 중 하나 이상이 1일 때 결과가 1이 됩니다.
  이를 기호로 표현하면 A OR B = A + B입니다.
• NOT 연산 : 입력 값이 1이면 결과가 0, 입력 값이 0이면 결과가 1이 됩니다.
  이를 기호로 표현하면 NOT A = ¬A 또는 A’입니다.

부울 대수의 역사는 조지 불(George Boole)의 작업에서 시작됩니다.
1854년에 그는 “The Laws of Thought”라는 책을 출판했으며, 이 책에서 부울 대수의 기본 원리를 설명했습니다.
조지 불은 논리적 사고를 수학적으로 표현할 수 있는 방법을 제시했으며, 이는 이후 컴퓨터 과학과 디지털 회로 설계의 근간이 되었습니다.

부울 대수 법칙은 이러한 기본 연산을 사용하여 복잡한 논리적 문제를 해결하는 데 사용됩니다.
예를 들어, “A가 참이고 B가 거짓이면 결과는?”과 같은 논리적 명제를 다룰 수 있습니다.
이러한 법칙은 수학적으로도 증명될 수 있으며, 이를 통해 디지털 시스템을 설계하고 분석하는 데 매우 유용합니다.

1-2) 전자 공학과 정보 통신에서의 부울 대수의 중요성

부울 대수 법칙은 전자 공학과 정보 통신 분야에서 매우 중요한 역할을 합니다.
현대의 거의 모든 디지털 시스템은 부울 대수의 원리를 기반으로 설계됩니다.

• 전자 공학에서의 중요성
  부울 대수는 디지털 회로의 설계와 분석에 필수적입니다.
  예를 들어, 컴퓨터의 중앙 처리 장치(CPU)는 수많은 논리 게이트로 구성되어 있으며, 이 게이트들은 부울 대수를 사용하여 논리적 연산을 수행합니다.
  간단한 예로, AND 게이트는 두 입력이 모두 참일 때만 참을 출력합니다.
  이러한 게이트들을 결합하여 더 복잡한 연산을 수행할 수 있으며, 이는 궁극적으로 컴퓨터가 데이터를 처리하고 계산을 수행하는 데 사용됩니다.
  
• 또한, 디지털 회로의 최적화에도 부울 대수 법칙이 활용됩니다.
  회로를 단순화하거나 최적화하려면 부울 대수 법칙을 사용하여 논리적 표현을 줄일 수 있습니다.
  예를 들어, A AND A는 A와 같다는 항등 법칙을 사용하여 중복된 연산을 제거할 수 있습니다.
  이는 회로의 크기를 줄이고, 전력 소비를 감소시키며, 성능을 향상시키는 데 도움이 됩니다.
  
• 정보 통신에서의 중요성
  부울 대수는 데이터 전송과 신호 처리에서도 중요한 역할을 합니다.
  예를 들어, 네트워크 라우터는 부울 대수 법칙을 사용하여 데이터 패킷이 목적지까지 올바르게 전달되도록 합니다.
  논리적 조건을 평가하고 데이터 경로를 결정하는 데 부울 대수의 원리를 적용할 수 있습니다.
  
• 또한, 암호화와 같은 데이터 보안 분야에서도 부울 대수가 사용됩니다.
  암호화 알고리즘은 데이터를 안전하게 보호하기 위해 복잡한 논리 연산을 사용하며, 이는 부울 대수 법칙에 기반을 둡니다.

부울 대수는 디지털 시스템 설계와 정보 통신의 핵심 요소입니다.
이는 전자 회로의 동작을 이해하고, 효율적인 시스템을 설계하는 데 필수적인 도구입니다.
부울 대수 법칙을 이해하고 적용하는 능력은 전자 공학과 IT 분야에서 성공적인 커리어를 구축하는 데 중요한 역할을 합니다.

• 연관 참조 : NAND 게이트 회로, 회로 구성, 특성과 성능, 장점 4개와 한계
• 연관 참조 : NOR 게이트 회로, 회로 구성, 특성 및 성능, 장점 3개와 한계
• 연관 참조 : XOR 게이트 회로 설계, 회로 구성, 특성 및 성능, 장점 3개와 한계
• 연관 참조 : XNOR 게이트 회로, 회로 구성, 특성과 성능, 장점 4개와 한계
• 연관 참조 : Buffer 회로 설계, 회로 설계의 기본 구성, 설계 고려 사항

2. 부울 대수의 기본 연산

부울 대수 법칙의 기본 연산은 AND, OR, NOT 세 가지로 구성됩니다.
이들은 각각 논리곱, 논리합, 부정 연산을 의미하며, 부울 대수 법칙의 기초를 형성합니다.

2-1) AND, OR, NOT 연산의 정의

2-1-1) AND 연산 (논리곱)

AND 연산은 두 입력이 모두 참(True)일 때만 결과가 참이 되는 연산입니다.
이 연산은 “둘 다”의 의미를 가지고 있습니다.
예를 들어, 두 조건 A와 B가 모두 참일 때만 결과가 참이 됩니다.
AND 연산은 보통 × 또는 · 기호로 표현되며, A AND B는 A × B 또는 A·B로 쓸 수 있습니다.

정의 : A * B = 1 (A = 1 그리고 B = 1 일 때만)
예제 :
A = 1, B = 1 → A * B = 1
A = 1, B = 0 → A * B = 0
A = 0, B = 1 → A * B = 0
A = 0, B = 0 → A * B = 0

2-1-2) OR 연산 (논리합)

OR 연산은 두 입력 중 하나라도 참이면 결과가 참이 되는 연산입니다.
이 연산은 “하나 이상”의 의미를 가지고 있습니다.
예를 들어, 두 조건 A와 B 중 하나라도 참이면 결과가 참이 됩니다.
OR 연산은 보통 + 기호로 표현되며, A OR B는 A + B로 쓸 수 있습니다.

정의 : A + B = 1 (A = 1 또는 B = 1 일 때)
예제 :
A = 1, B = 1 → A + B = 1
A = 1, B = 0 → A + B = 1
A = 0, B = 1 → A + B = 1
A = 0, B = 0 → A + B = 0

2-1-3) NOT 연산 (부정)

NOT 연산은 입력 값의 반대 값을 출력하는 연산입니다.
즉, 입력 값이 참이면 결과는 거짓이고, 입력 값이 거짓이면 결과는 참이 됩니다.
NOT 연산은 보통 아래처럼 A바 기호로 표현되며, NOT A바 또는 A’로 쓸 수 있습니다.

정의 : A바 = 1 (A = 0 일 때)
예제 :
A = 1 → A바 = 0
A = 0 → A바 = 1

2-2) 진리표와 연산 예제

부울 대수 법칙의 기본 연산을 이해하는 데 진리표가 매우 유용합니다.
진리표는 모든 가능한 입력 조합에 대한 출력을 명확하게 보여줍니다.

2-2-1) AND 연산 진리표

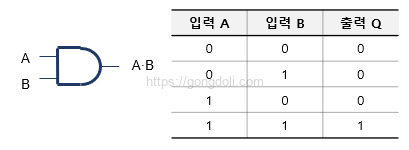
예를 들어, LED가 켜지려면 두 개의 스위치(A, B)가 모두 켜져야 한다고 가정해 보겠습니다.
이 경우 AND 연산은 두 스위치가 모두 켜졌을 때만 LED가 켜진다는 것을 보여줍니다.

2-2-2) OR 연산 진리표

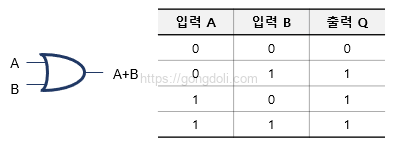
예를 들어, 집에 두 개의 문이 있다고 가정해 보겠습니다.
한개의 문이라도 열려 있으면 경보 시스템이 작동한다고 할 때, OR 연산은 두 문 중 하나라도 열리면 경보가 울린다는 것을 보여줍니다.

2-2-3) NOT 연산 진리표

예를 들어, 전등의 상태가 스위치의 반대라고 가정해봅시다.
스위치가 켜지면 전등이 꺼지고, 스위치가 꺼지면 전등이 켜지는 상황입니다.
이 경우 NOT 연산은 스위치와 전등의 상태가 반대라는 것을 보여줍니다.

3. 부울 대수 법칙의 예제

3-1) 예제1

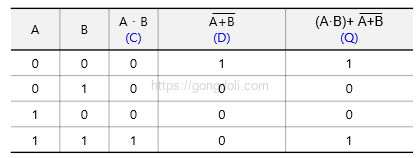
주어진 회로에서 점 C, D, Q의 논리적 함수에 대한 진리표를 작성하고, 전체 회로를 대체할 수 있는 단일 논리 게이트를 식별해 보겠습니다.

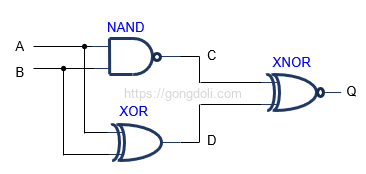
논리식을 구해보기 위해 회로의 각 점에서의 출력을 부울 대수로 표현해 보겠습니다.

점 C (A NAND B) : 점 C의 출력은 입력 A와 B의 NAND 연산 결과입니다.
NAND 연산은 AND 연산 후 결과를 NOT 연산하는 것입니다.

점 D (A XOR B) : 점 D의 출력은 입력 A와 B의 XOR 연산 결과입니다.
XOR 연산은 두 입력이 서로 다를 때만 결과가 참이 됩니다.

XOR 연산은 A와 B가 같지 않을 때 1을 출력합니다.

점 Q (C XNOR D) : 점 Q의 출력은 점 C와 D의 XNOR 연산 결과입니다.
XNOR 연산은 두 입력이 같을 때 결과가 참이 됩니다.

XNOR 연산은 두 입력이 동일할 때 1을 출력합니다.

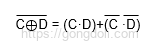
입력 A와 B의 모든 가능한 값을 나열하고, 각 값에 대한 C, D, Q의 출력을 계산하여 진리표를 작성해 보겠습니다.

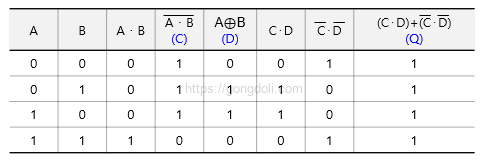
다음으로 전체 회로를 단일 논리 게이트로 대체할 수 있는지 확인하려면 Q에 대한 표현을 단순화해야 합니다.

C와 D의 조합으로 XNOR 연산을 수행합니다.
XNOR 연산은 두 입력이 같을 때 참입니다.
여기서 C와 D는 항상 같지 않음을 확인할 수 있습니다 (진리표에서 C와 D가 동일한 값이 없음).

따라서 Q의 표현은

이며, 이는 XNOR 연산의 결과입니다. 이 경우, Q는 항상 1이 됩니다.

3-2) 예제2

다음 시스템에 대한 부울 대수식을 구합니다.

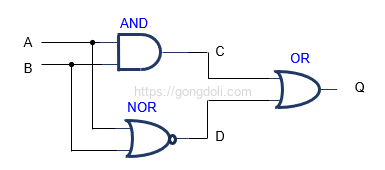
AND 게이트

AND 게이트는 입력 A와 B가 모두 참일 때만 참(True)을 출력합니다.
따라서 AND 게이트의 출력은 다음과 같습니다:

C=A⋅B

NOR 게이트

NOR 게이트는 입력 A와 B가 모두 거짓(False)일 때만 참(True)을 출력합니다.
이는 OR 게이트의 출력에 NOT 연산을 적용한 결과입니다.
따라서 NOR 게이트의 출력은 다음과 같습니다.

OR 게이트

OR 게이트는 하나 이상의 입력이 참일 때 참(True)을 출력합니다.
이 회로에서는 AND 게이트의 출력(C)와 NOR 게이트의 출력(D)을 입력으로 받습니다.
OR 게이트의 최종 출력은 다음과 같습니다.

• Q=C+D
• 여기서 C와 D를 대입하면,

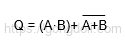
이제 부울 대수 표현 Q를 단순화해 보겠습니다.

De Morgan의 법칙 적용하면,

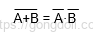
따라서,

이 식은 A와 B가 모두 1이거나, A와 B가 모두 0일 때만 참입니다.

이 식을 추가로 단순화하기 위해서는 추가적인 논리 게이트가 필요할 수 있지만, 현재 표현은 최종 형태로 간주할 수 있습니다.
즉, 이 식은 AND와 NOR 연산의 결과를 OR 게이트로 결합한 가장 간단한 형태입니다.

회로는 입력 A와 B가 모두 참이거나 모두 거짓일 때 참(True)을 출력합니다.