Contents
1. 개요
상호 인덕턴스는 전기와 자기의 상호 작용을 설명하는 개념 중 하나입니다.
두 개 이상의 코일이 서로 가까이 위치하고 있을 때, 한 코일에 흐르는 전류가 다른 코일에 전기적으로 유도되는 현상을 나타냅니다.
예를 들어, 한 코일에 전류를 흐르게 하면 주변에 자기장이 형성됩니다.
이 자기장은 다른 코일을 통해 흘러갈 수 있습니다.
이때, 첫 번째 코일의 전류가 변화하면, 그 주변의 자기장도 변화하게 되고, 이 변화된 자기장은 두 번째 코일을 통해 전류를 유도합니다.
이러한 상호 작용을 상호 인덕턴스라고 합니다.
상호 인덕턴스는 1831년에 영국의 과학자인 마이클 패러데이(Michael Faraday)에 의해 발견되었습니다.
그는 자기장의 변화가 전류를 유도한다는 것을 발견했고, 이를 상호 인덕턴스라고 명명했습니다.
이후에는 맥스웰(Maxwell)의 전자기학 이론에 의해 상호 인덕턴스의 이론적인 기초가 확립되었습니다.
- 연관 참조 : 인덕터 특성, 코어의 종류, 구조와 동작원리, 특성 4가지,선택 주의 사항
- 연관 참조 : 코일의 인덕턴스,예제 2개, 선택 고려 사항
- 연관 참조 : 나선형 코일 인덕턴스 계산기,Helical coil inductance calculator, 사용 방법
- 연관 참조 : 유도 리액턴스,정의,위상 다이어그램, 주요 문제 및 해결책 4가지
- 연관 참조 : 직렬 인덕터,정의, 예제, 병렬 분류,분류에 따른 예제 2개
- 연관 참조 : 병렬 인덕터, 정의, 공식, 예제 3개
- 연관 참조 : 플레밍의 왼손 법칙과 오른손 법칙, 이해, 차이점
- 연관 참조 : 패러데이 전자기 유도,패러데이 실험, 1법칙, 2법칙, 차이점, 중요성
- 연관 참조 : 렌츠의 법칙, 동작 원리, 패러데이 법칙과 차이
2. 상호 인덕턴스 원리
2-1) 원리
상호 인덕턴스는 두 개의 자석으로 연결된 코일 간의 회로 파라미터로, 한 코일이 생성한 변화하는 자속이 인접한 두 번째 코일로 유도되는 비율을 정의합니다.
이전에 우리는 인덕터가 자체 코일 턴 주변의 변하는 자기장으로 인해 자기 유도 전압을 생성한다고 보았습니다.
이 전압이 전류가 변하는 동일한 회로에 유도될 때 이 효과는 자기 유도 (L)라고 합니다.
그러나 이 전압이 같은 자기장 안에 있는 인접한 코일에 유도되면, 이 전압은 자기적으로 유도되거나 상호적으로 유도되거나 상호 유도라고도 합니다 (M).
그럼 두 개 이상의 코일이 공통 자속에 의해 자기적으로 연결될 때 상호 인덕턴스의 속성이 있다고 말합니다.
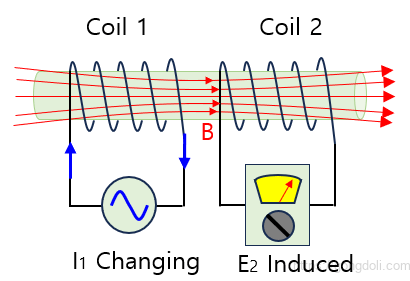
상호 인덕턴스는 변압기, 모터, 발전기 및 다른 자기장과 상호 작용하는 모든 전기 부품의 기본 동작 원리입니다.
그런 다음 상호 유도를 한 코일에서 흐르는 전류로 정의할 수 있습니다.
상호 인덕턴스는 때때로 문제가 될 수 있습니다.
“유출” 인덕턴스란 코일이 다른 부품에 불필요하게 자기장을 전달하는 현상을 말합니다.
이러한 유출 인덕턴스는 인접한 다른 부품의 동작을 방해할 수 있습니다.
간단히 말하면, 코일은 자기장을 생성합니다.
이 자기장이 다른 부품에 영향을 줄 수 있습니다.
때로는 이러한 영향이 원하지 않는 부분으로 전달되어 다른 부품의 동작을 방해할 수 있습니다.
이를 막기 위해 전기적으로 화면 처리를 하거나, 코일을 설계할 때 유출 인덕턴스를 최소화하는 방법을 사용합니다.
이렇게 함으로써 인접한 부품들 사이의 상호 작용을 최소화하고 원활한 전기적 시스템 동작을 유지할 수 있습니다.
한 코일에서 다른 코일로의 상호 인덕턴스 양은 두 코일의 상대적 위치에 매우 의존합니다.
한 코일이 다른 코일 옆에 위치하여 물리적 거리가 가까우면, 첫 번째 코일에서 생성된 거의 모든 자속이 두 번째 코일의 코일 턴과 상호 작용하여 상대적으로 큰 유도 전압을 유도하고 따라서 상대적으로 큰 상호 인덕턴스 값을 생성합니다.
마찬가지로, 두 코일이 서로 더 멀리 떨어져 있거나 서로 다른 각도에 위치하면, 첫 번째 코일에서 두 번째로 유도되는 자속의 양은 약해져서 훨씬 작은 유도 전압을 유도하고 따라서 훨씬 작은 상호 인덕턴스 값을 생성합니다.
따라서 상호 인덕턴스의 영향은 두 코일의 상대적인 위치나 간격에 크게 의존합니다.
2-2) 상호 인덕턴스 공식
코일 1인 L1에 흐르는 전류는 자기장을 형성하며, 이 자기장의 일부는 코일 2인 L2를 통과하여 상호 인덕턴스를 생성합니다.
코일 1에는 I1 전류와 N1 개의 턴이 있고, 코일 2에는 N2 개의 턴이 있습니다.
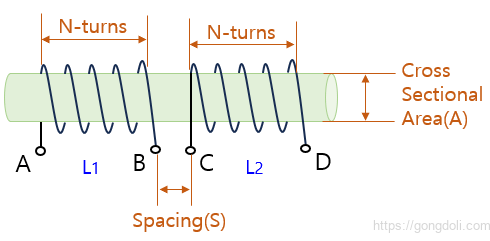
따라서 코일 2의 코일 1에 대한 Mutual Inductance M12는 서로의 위치에 따라 달라지며 다음과 같이 주어집니다
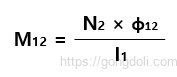
- 여기서,
- N2는 코일 2의 턴 수
- Φ12는 코일 1의 전류 I1이 생성하는 자속
마찬가지로, 코일 2에서 전류가 흐를 때 코일 1을 둘러싼 자기 플럭스는 코일 1에서 같은 전류가 흐를 때 코일 2를 둘러싼 자속과 정확히 같습니다.
따라서 코일 1의 코일 2에 대한 상호 인덕턴스는 M21로 정의됩니다.
이 상호 인덕턴스는 두 코일의 크기, 턴 수, 상대적 위치 또는 방향에 관계없이 참입니다.
이것 때문에 우리는 두 코일 간의 상호 인덕턴스를 다음과 같이 쓸 수 있습니다
M12=M21=M
따라서 자체 인덕턴스는 인덕터를 단일 회로 요소로 특성화하며, Mutual Inductance는 두 인덕터 또는 코일 간의 어떤 형태의 자기적 결합을 나타냅니다.
이는 그들의 거리와 배열에 따라 다릅니다.
또한, 각각의 코일의 자체 인덕턴스는
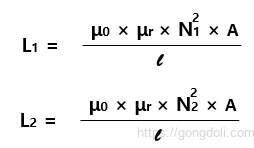
- 여기서,
- N은 턴 수
- μ는 자기 투자율
- A는 횡단면적
- l은 길이
위의 두 방정식을 교차하여, 두 코일 사이에 존재하는 상호 인덕턴스 M는 각 코일의 자기 자속으로 표현될 수 있다.
두 코일 사이의 Mutual Inductance를 나타내는 최종적이고 보다 일반적인 표현은
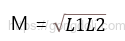
3. 상호 인덕턴스 결합 계수
위의 방정식은 두 코일 간의 Mutual Inductance를 100%의 자기적 결합과 제로 플럭스(zero flux) 유출로 가정합니다.
그러나 실제로는 항상 플럭스 유출과 위치에 따른 손실이 발생하므로, 두 코일 간의 자기적 결합은 100%를 초과할 수 없습니다.
이러한 경우 특별한 인덕티브 코일에서는 이 값이 매우 근접할 수 있습니다.
두 코일 간의 자기적 결합을 설명할 때, 총 자기 플럭스 중 일부가 두 코일에 링크되는 상황을 고려해야 합니다.
이렇게 링크된 플럭스의 양은 두 코일 간의 총 가능한 플럭스 링크의 일부로 정의됩니다.
이 분수값은 결합 계수(coefficient of coupling)라고 하며, 보통 k로 표기됩니다.
결합 계수(k)는 두 코일 간의 자기적 결합 정도를 나타내는 중요한 개념입니다.
이 값은 0과 1 사이의 수로 표현되며, 0은 두 코일 간의 아무런 결합이 없음을 의미하고, 1은 완전한 결합을 의미합니다.
따라서 결합 계수가 클수록 두 코일은 강하게 상호 작용하고, 작을수록 상호 작용이 약해집니다.
다시 말해, 결합 계수(k)가 1이면 두 코일은 완벽하게 결합되어 있습니다.
k가 0.5보다 크면 코일 간의 결합이 강하고, k가 0.5보다 작으면 코일 간의 결합이 약하다고 말할 수 있습니다.
그럼 위의 방정식은 이 결합 계수 k를 고려하도록 수정할 수 있습니다.
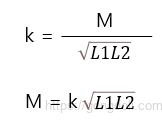
결합 계수 k가 1인 경우, 한 코일의 모든 자기장 선이 다른 코일의 모든 턴을 통과합니다.
이는 두 코일이 매우 강하게 결합되어 있음을 의미합니다.
이 때, 두 코일 간의 상호 인덕턴스는 각 코일의 인덕턴스 값의 기하 평균이 됩니다.
기하 평균은 여러 값의 곱을 취한 후에 모든 값들의 개수로 제곱근을 구하는 것입니다.
또한, 두 코일의 인덕턴스가 서로 동일하고 L1=L2인 경우, 두 코일 간의 Mutual Inductance는 한 코일의 값과 같아집니다.
이는 두 코일 간의 상호 작용이 서로 동등하고 균형을 이루고 있음을 의미합니다.
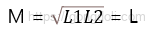
4. 예제 풀이
4-1) 예제 1
자기 인덕턴스가 각각 75mH와 55mH로 주어진 두 개의 인덕터는 첫 번째 코일에서 나오는 선속의 75%가 두 번째 코일을 절단하도록 공통의 자기 코어 위에 나란히 위치합니다. 두 코일 사이에 존재하는 총 상호 인덕턴스를 계산해 보겠습니다. ㅁ
문제에 두 인덕터의 자기 자속이 각각 75mH와 55mH로 주어졌고, 제 1 코일의 자기력선의 75%가 두 번째 코일을 통과한다고 가정합니다.
두 코일 사이에 존재하는 총 상호 인덕턴스
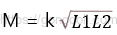
첫 번째 코일의 자기력선 중 75%가 두 번째 코일을 통과한다고 하면, 결합 계수 k는 0.75로 정의됩니다.
두 코일의 자기 자속은 각각 L1=75 mH와 L2=55 mH입니다.
주어진 값들을 공식에 대입하면
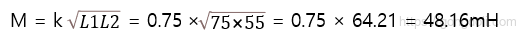
4-2) 예제 2
각각 5H, 4H의 인덕턴스를 가지는 두 코일을 비자성체 코어에 균일하게 감았을 때, 이들의 상호 인덕턴스는 1.5H로 나타났습니다.
이들 사이에 존재하는 커플링 계수를 계산해 보겠습니다.
두 코일의 상호 인덕턴스 M이 1.5 H이며, 두 코일의 자기 자속이 각각 L1=5H와 L2=4 H입니다.
결합 계수 k를 계산하기 위해
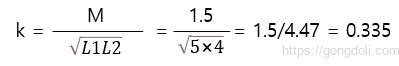
따라서, 두 코일 간에 존재하는 결합 계수는 약 0.335입니다.
5. 자기 인덕턴스와 비교
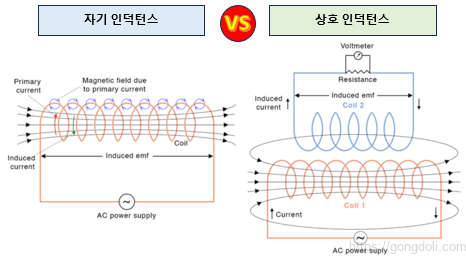
| 구분 | 자기 인덕턴스 (Self-Inductance) | 상호 인덕턴스 (Mutual Inductance) |
|---|---|---|
| 정의 | 단일 회로 요소 내에서 발생하는 자기장에 의한 전류 변화에 의한 전압 발생 | 두 개 이상의 회로 요소 간의 상호 작용으로 인한 자기장에 의한 전압 발생 |
| 적용 | 단일 회로 요소 (인덕터) | 두 개 이상의 인덕터 또는 코일 간의 관계 |
| 특징 | 자기장은 동일한 회로 요소 내에서 발생함 | 두 개 이상의 회로 요소 간에 발생함 |
| 영향 | 전류의 변화 속도에 따라 변함 | 두 코일 사이의 위치와 회로 요소 간의 상호 작용에 따라 변함 |
| 수식 | V=L*di/dt | V=M*di/dt (두 코일 간) |
| 예시 | 단일 인덕터 | 트랜스포머, 상호 인덕턴스 측정 |
| 관련 회로 요소 | 인덕터, 트랜스포머, 코일 등 |

I have learn several good stuff here. Certainly value bookmarking for revisiting. I surprise how much attempt you place to make such a great informative site.
Thank you so much! I’m glad you found the content valuable, and your support means a lot
I gotta bookmark this website it seems extremely helpful extremely helpful
Thank you so much! I’m truly glad you’re finding the site helpful.
I’ll keep doing my best to share content that’s worth bookmarking!
Have you ever considered writing an e-book or guest authoring on other sites? I have a blog based upon on the same subjects you discuss and would really like to have you share some stories/information. I know my readers would enjoy your work. If you are even remotely interested, feel free to send me an email.
Thank you so much for the kind invitation!
I’m truly honored that you thought of me. At the moment, I’m quite tied up with other commitments, so unfortunately I won’t be able to contribute right now.
I really appreciate your interest, and I hope we can connect again in the future!
I really like your writing style, great info, regards for putting up :D. “All words are pegs to hang ideas on.” by Henry Ward Beecher.
Thank you so much!
I like what you guys are up too. Such smart work and reporting! Keep up the excellent works guys I’ve incorporated you guys to my blogroll. I think it’ll improve the value of my web site 🙂
Thank you so much, that truly means a lot!
We’re thrilled to be part of your blogroll, and it’s amazing to hear that you find value in what we do.
I would like to thank you for the efforts you’ve put in writing this website. I’m hoping the same high-grade site post from you in the upcoming as well. Actually your creative writing skills has encouraged me to get my own website now. Actually the blogging is spreading its wings rapidly. Your write up is a good example of it.
Thank you so much for your kind words!
I’m truly honored that my writing inspired you to start your own website — that’s one of the best compliments I could receive.
Good write-up, I’m regular visitor of one’s website, maintain up the excellent operate, and It is going to be a regular visitor for a long time.
Thank you so much for your continued support—it truly means a lot!
I’m thrilled to know you’re a regular visitor
Deference to article author, some great selective information.
Much appreciated—glad the info stood out!
After examine a couple of of the weblog posts on your web site now, and I really like your approach of blogging. I bookmarked it to my bookmark web site checklist and will probably be checking back soon. Pls check out my site as well and let me know what you think.
Thanks a lot—I’ll try to check out your site soon!
Superb blog! Do you have any tips and hints for aspiring writers? I’m planning to start my own website soon but I’m a little lost on everything. Would you recommend starting with a free platform like WordPress or go for a paid option? There are so many options out there that I’m totally confused .. Any tips? Cheers!
Starting simple is best—free platforms help you learn before investing in paid options.
hello!,I love your writing very so much! share we communicate extra approximately your post on AOL? I need a specialist on this area to unravel my problem. Maybe that’s you! Looking forward to peer you.
Thank you for your kind words.
I couldn’t resist commenting
Thank you for taking the time to comment.