Contents
1. 수동 RC 고역 통과 필터란?
수동 RC 고역 통과 필터는 저주파 신호를 약화하거나 차단하면서 고주파 신호를 통과시키는 회로입니다.
저항 및 커패시터와 같은 수동 구성 요소로 구성되어 있습니다.
이 필터에서 커패시터는 입력 신호와 직렬로 연결되어 있으며 출력은 저항을 통해 취합니다.
필터의 동작은 커패시터의 주파수 종속 반응(리액턴스)과 저항의 특성에 의해 결정됩니다.
고주파에서는 커패시터의 리액턴스가 감소하여 회로를 통해 더 많은 전류가 흐르게 되지만, 저주파에서는 리액턴스가 증가하여 전류의 흐름이 차단됩니다.
이렇게 주파수에 따른 반응은 필터가 고주파 신호를 비교적 영향을 받지 않고 통과시키는 동시에 저주파 신호를 약화시키는 것으로 이어집니다.
패시브 RC 하이 패스 필터는 오디오 시스템, 통신 회로 및 전자 장치에서 유용한 고주파 신호를 통과시키면서 원치 않는 저주파 노이즈와 간섭을 제거하기 위해 널리 사용됩니다.
신호 처리 및 주파수 선택 응용 프로그램에서 중요한 구성 요소입니다.
- 연관 참조 : 용량성 리액턴스, 원리, 예제 3개, 그래프
- 연관 참조 : RC 수동 저역 통과 필터,출력 전압 계산,예제2,주파수 응답,2차 LPF 주파수 응답
- 연관 참조 : RL 수동 저역 통과 필터, LPF 종류,동작 원리,상한 차단 주파수, 예제1
- 연관 참조 : 수동 대역 통과 필터란?, RLC을 사용한 BPF회로,주파수 응답, 예제1,요약
- 연관 참조 : 능동 저역 통과 필터,1차 LPF, 전압 이득, 예제1
2. 이상적인 고역 통과 필터
이상적인 RC 고역 통과 필터는 저항과 커패시터가 직렬로 연결된 회로입니다.
이 필터는 주로 저주파수를 차단하고 고주파수를 통과시키는 역할을 합니다.
이상적인 필터에서는 커패시터와 저항의 특성만을 고려하며, 임피던스가 무한대로 가정됩니다.
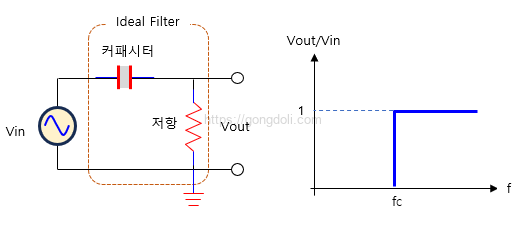
고역 통과 필터의 주요 특징은 커트오프 주파수 (Fc)입니다.
이 주파수는 필터가 입력 신호를 차단하기 시작하는 지점을 나타냅니다.
이상적인 필터에서는 Fc 이상의 주파수는 완전히 통과되고, Fc 이하의 주파수는 완전히 차단됩니다.
이상적인 RC 고역 통과 필터의 전압-주파수 응답은 Fc에서 급격한 하강을 보이며, 이 상태에서 주파수가 증가함에 따라 출력 전압이 점차 감소합니다.
이는 커패시터의 특성 때문에 발생하는데, 고주파수에서 커패시터의 임피던스가 감소하여 입력 신호를 차단합니다.
이상적인 필터는 실제 회로에서 발생하는 불완전성을 고려하지 않으며, 임피던스의 영향을 무시합니다.
따라서 실제 회로에서는 이상적인 특성을 완벽하게 구현하기 어렵습니다.
그러나 이상적인 필터의 이론적인 특징을 이해하는 것은 실제 필터 회로의 동작을 이해하는 데 큰 도움이 됩니다.
3. Real RC 고역 통과 필터
Real RC 고역 통과 필터는 이상적인 필터와 달리 실용적인 고려 사항과 한계로 인해 일부 불완전함과 제한이 있습니다.
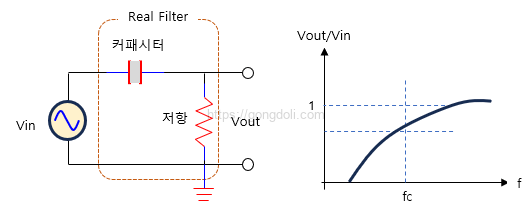
- 부품 허용 오차: 현실 세계의 회로에서 저항기와 커패시터는 허용 오차를 가지고 있습니다.
이는 제조업체에서 명시한 명목값에서 약간 벗어날 수 있음을 의미합니다.
이러한 허용 오차는 필터의 차단 주파수 및 전체 성능에 영향을 줄 수 있습니다. - 부품의 비이상적 동작: 실제 커패시터는 직렬 저항(ESR) 및 동등 직렬 인덕턴스(ESL)와 같은 기생 요소를 가지고 있으며, 실제 저항기는 고주파에서 기생용량 및 인덕턴스를 가질 수 있습니다.
이러한 비이상성은 고주파에서 부가적인 임피던스 요소를 도입하여 필터의 주파수 응답에 영향을 줄 수 있습니다. - 주파수 의존적 특성: 저항기와 커패시터 모두 주파수 의존적인 특성을 나타냅니다.
예를 들어, 커패시터는 주파수에 따라 용량이 변할 수 있으며, 저항기는 고주파에서 기생용량과 인덕턴스를 나타낼 수 있습니다.
이러한 주파수 의존적인 효과는 이상적인 필터 응답에서의 벗어남을 일으킬 수 있습니다. - 부하 효과: 고역 통과 필터의 동작은 출력에 연결된 부하의 임피던스에 영향을 받을 수 있습니다.
만약 부하 임피던스가 필터의 출력 임피던스에 비해 충분히 높지 않다면, 필터의 차단 주파수 및 감쇠 특성에 영향을 줄 수 있습니다. - 온도 의존성: 전자 부품의 특성은 온도에 따라 다를 수 있습니다.
온도의 변화는 저항기와 커패시터의 값에 영향을 줄 수 있으며, 결과적으로 특정 온도에서 필터의 성능에 변화를 일으킬 수 있습니다.
전반적으로, 이상적인 RC 고역 통과 필터는 필터 원리를 이해하기 위한 이론적 모델로 작용하지만, 현실 세계에서의 구현은 특정 응용에 대한 원하는 성능을 달성하기 위해 이러한 실용적인 제한 사항을 신중하게 고려해야 합니다.
4. 1차 고역 통과 필터의 주파수 응답
주파수 응답과 커패시터 반응에 대한 곡선은 다음과 같습니다
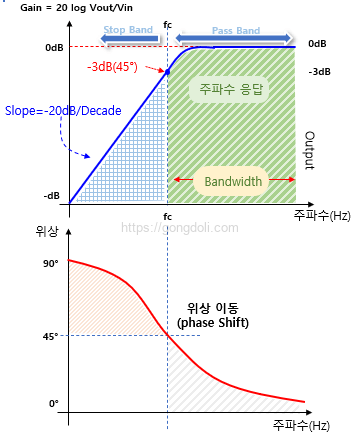
이 곡선은 고주파 필터가 저주파 필터와 정반대라는 것을 보여줍니다.
고주파 필터는 차단 주파수보다 낮은 주파수의 신호를 차단하고 출력 전압을 줄입니다.
차단 주파수에서 저항 ‘R’의 값과 커패시터 ‘X_c’의 반응이 동일해지면 출력 전압이 -20 dB/decade의 속도로 증가하고 출력 신호 레벨은 입력 신호 레벨의 -3 dB입니다.
매우 높은 주파수에서 커패시터 반응이 제로가 되면 출력 전압은 입력 전압과 동일해집니다.
낮은 주파수에서는 커패시터 반응이 무한대이므로 커패시터에 진입하는 전류를 차단하여 출력 전압이 제로입니다.
고주파 필터의 출력은 입력 신호에 대해 +45°의 위상 변화를 갖습니다.
이것은 고주파 필터의 출력이 입력 신호에 앞선다는 것을 의미합니다.
고주파에서 (f > fC) 위상 변화는 거의 제로이므로 입력 및 출력 신호가 동일합니다.
이상적인 경우, 필터는 차단 주파수 지점 이후의 주파수를 무한대로 허용하지만, 실제로는 무한대 값이 필터 설계에 사용된 구성 요소 값에 따라 다릅니다.
커패시터의 충전 및 방전 시간은 입력 신호와의 상대적인 위상 차이를 유발합니다.
커패시터와 직렬로 연결된 저항은 충전 및 방전 효과를 생성합니다.
직렬 RC 회로의 시간 상수는 커패시터가 최종 정상 상태 값의 63.2%로 충전하는 데 걸리는 시간으로 정의되며, 이는 커패시터가 정상 상태 값의 36.8%로 방전하는 데 걸리는 시간으로 정의됩니다.
이것은 ‘τ’ 기호로 표시됩니다.
시간 상수와 차단 주파수 간의 관계는 다음과 같습니다.
시간 상수 τ=RC= 1⁄2πfc 및 ω_c= 1/τ = 1/RC.
이로써 필터의 출력이 입력에 적용된 주파수 및 시간 상수에 의존함을 알 수 있습니다.
차단 주파수는?
fc = 1/ 2πfc
위상 변화 (ø) = tan-1 (2πfRc)
5. 고역 통과 필터 출력 전압 및 게인
RC 고역 통과 필터의 출력 전압 및 이득은 다음과 같은 수식으로 나타낼 수 있습니다
출력 전압 (Vout)는 RC 고역 통과 필터의 출력 전압은 입력 전압 (Vin)과 다음과 같은 비율로 결정됩니다.
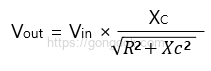
여기서 Xc는 커패시터의 적응저항을 나타냅니다.
이 수식은 커패시터와 저항으로 구성된 전기 회로에서 출력 전압을 계산하는데 사용됩니다.
이득 (Gain)은 RC 고역 통과 필터의 이득은 출력 전압과 입력 전압의 비율로 정의됩니다.
이것은 다음과 같이 표현될 수 있습니다
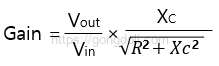
이 수식은 필터의 주파수 응답을 설명하는데 사용됩니다.
낮은 주파수에서 이득은 작고, 높은 주파수에서는 증가합니다.
이 수식들은 주파수 응답 및 전압 증폭 특성을 분석하는데 사용됩니다.
일반적으로 RC 고역 통과 필터의 출력 전압 및 이득은 입력 주파수 및 회로 구성 요소에 따라 변화하므로 이러한 수식은 설계 및 분석에 중요합니다.
5. 고역 통과 필터 예제
82pF 커패시터가 240kΩ 저항과 직렬로 연결된 간단한 수동 고역 통과 필터의 차단 주파수 (ƒc)를 계산해보겠습니다.
수동 고역 통과 필터의 차단 주파수 (ƒc)를 계산하기 위해 다음 공식을 사용할 수 있습니다.
ƒc = 1 / (2πRC)
주어진 값:
- R=240kΩ=240×103Ω
- C=82pF=82×10−12F
ƒc = 1 / (2π×240×103×82×10−12) ≈ 8087Hz ≈ 8KHz
따라서 주어진 수동 고역 통과 필터의 차단 주파수 (ƒc)는 약 8KHz입니다.
6. 2차 고역 통과 필터
2차 고역 통과 필터는 저역 통과 필터와 유사하지만, 저역 통과 필터의 반대 기능을 합니다.
이 필터는 저역 주파수를 허용하지 않고 고역 주파수를 통과시킵니다.
두 개의 반응성 요소(일반적으로 커패시터)와 한 개의 저항으로 구성되며, 일반적으로 “T” 모양의 구성으로 설계됩니다.
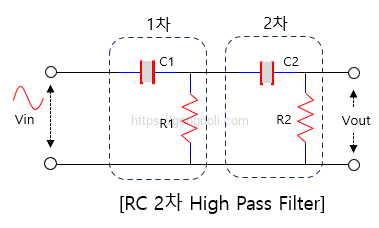
이 필터의 주요 특징 중 하나는 1차 필터와 달리 40dB/decade의 기울기를 가지고 있다는 것입니다.
이는 주파수가 두 배로 증가할 때 출력 신호의 크기가 40dB(또는 12dB/octave)씩 감소한다는 것을 의미합니다.
2차 고역 통과 필터의 주파수 응답은 저역 통과 필터와 정반대로 됩니다.
즉, 고역 주파수에서 저역 주파수로 향하는 경사가 있습니다.
이는 저역 주파수에서 고역 주파수로 신호의 크기가 급격하게 증가한다는 것을 의미합니다.
단일 단계 고역 통과 필터와 비교하여 더 효율적입니다.
왜냐하면 두 개의 저장 점을 갖기 때문입니다.
두 단계 필터의 차단 주파수는 두 개의 커패시터와 두 개의 저항 값에 따라 결정됩니다.
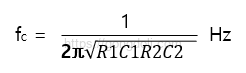

You are my inspiration, I own few web logs and infrequently run out from post :). “To die for a religion is easier than to live it absolutely.” by Jorge Luis Borges.
Thank you so much for your kind words!
Only wanna remark on few general things, The website style and design is perfect, the written content is real excellent. “Some for renown, on scraps of learning dote, And think they grow immortal as they quote.” by Edward Young.
Thank you so much for your thoughtful feedback and for sharing that brilliant quote from Edward Young!
I’m delighted that you enjoyed both the design and the content—it truly means a lot.
I?¦ll immediately grab your rss as I can’t to find your email subscription link or e-newsletter service. Do you have any? Kindly allow me know so that I may subscribe. Thanks.
Thank you so much for your interest!
I’m thrilled you’d like to subscribe. At the moment, I don’t have an email subscription or newsletter service set up,
but RSS is a great way to stay updated.
If I launch a newsletter in the future, I’ll be sure to let you know!
Oh my goodness! an incredible article dude. Thank you Nonetheless I am experiencing problem with ur rss . Don’t know why Unable to subscribe to it. Is there anyone getting an identical rss drawback? Anybody who is aware of kindly respond. Thnkx
Thank you so much for your kind words—I’m really glad you enjoyed the article!
Sorry to hear you’re having trouble with the RSS feed.
Keep functioning ,terrific job!
Thank you so much!
Hiya, I am really glad I’ve found this information. Today bloggers publish only about gossips and internet and this is really annoying. A good website with interesting content, that’s what I need. Thank you for keeping this site, I will be visiting it. Do you do newsletters? Cant find it.
Thank you so much for your kind words!
As for newsletters—there isn’t one available at the moment, but I appreciate your interest.
Hi my friend! I want to say that this article is amazing, nice written and include almost all significant infos. I would like to see more posts like this.
Thanks a lot—more posts like this are definitely on the way!
I conceive you have observed some very interesting details , thankyou for the post.
Appreciate that—thanks for reading!
It?¦s in reality a great and helpful piece of info. I am glad that you simply shared this helpful information with us. Please stay us up to date like this. Thanks for sharing.
I’ll do my best to keep it updated.
Your style is so unique compared to many other people. Thank you for publishing when you have the opportunity,Guess I will just make this bookmarked.2
Thank you! I’m glad you appreciate the unique style and want to bookmark the site.
That is the proper weblog for anyone who wants to find out about this topic. You understand a lot its virtually arduous to argue with you (not that I actually would want…HaHa). You definitely put a brand new spin on a subject thats been written about for years. Nice stuff, just great!
Thank you for your kind words. I’m glad you found the post refreshing and enjoyable.