Contents
1. 수정 발진기란?
1-1) 수정 발진기의 정의와 기본 원리
수정 발진기는 수정 크리스털(Quartz)을 사용하여 매우 안정적인 진동을 만들어내는 전자 장치입니다.
이때 수정 크리스털은 기계적인 변형에 따라 전압을 생성하는 압전 효과(piezoelectric effect)를 이용합니다.
쉽게 말해, 수정 크리스털이 전압을 받으면 진동하고, 그 진동을 통해 특정한 주파수를 얻어내는 방식입니다.
수정 발진기 원리를 조금 더 자세히 설명하면, 전압이 가해진 수정 크리스털이 특정한 주파수로 기계적으로 진동합니다.
그리고 이 진동이 다시 전기 신호로 변환되면서, 우리가 원하는 주파수를 생성할 수 있는 것입니다.
이 주파수는 매우 안정적이며, 외부 환경(온도나 전압 변화)에 큰 영향을 받지 않습니다.
그래서 시계처럼 시간이 매우 정확해야 하는 장비에 널리 쓰입니다.
1-2) 일반 발진기와의 차이점
그렇다면 수정 발진기와 일반 발진기 사이에는 어떤 차이점이 있을까요?
대부분의 발진기는 LC 회로(인덕터와 커패시터를 사용한 발진기)나 RC 회로(저항과 커패시터를 사용한 발진기)를 사용하여 주파수를 생성합니다.
이 방식은 상대적으로 간단하지만, 주파수의 안정성 면에서 한계가 있습니다.
온도 변화나 외부 환경에 따라 주파수가 쉽게 변동될 수 있기 때문이죠.
반면에, 수정 발진기 원리는 수정 크리스털을 이용해 매우 정확하고 일정한 주파수를 생성하기 때문에, 주파수 안정성 면에서 압도적인 성능을 보여줍니다.
이러한 이유로 수정 발진기는 고정밀도가 요구되는 기기에서 필수적으로 사용됩니다.
자주하는 질문 중 하나가 “수정 발진기와 LC 발진기의 차이점이 무엇인가요?”라는 질문입니다.
그 답은 바로 주파수의 안정성에서 찾을 수 있습니다.
LC 발진기는 비교적 간단하게 만들 수 있지만, 주파수가 외부 환경에 따라 변동하는 반면, 수정 발진기는 수정 크리스털의 물리적 특성 덕분에 매우 안정적인 주파수를 유지할 수 있습니다.
1-3) 수정 발진기가 널리 사용되는 이유
수정 발진기는 왜 이렇게 많은 전자 기기에 사용될까요?
그 이유는 다음과 같은 특징 때문입니다
- 높은 주파수 안정성 : 위에서 언급한 것처럼, 수정 발진기는 온도, 전압 변화에 크게 영향을 받지 않습니다.
따라서 안정적인 주파수를 오랜 기간 유지할 수 있습니다.
이는 정확한 시간이 필요한 시계나 컴퓨터, 정밀 통신 장비에서 매우 중요한 요소입니다. - 소형화 가능: 수정 크리스털은 물리적으로 작은 크기로도 높은 성능을 발휘할 수 있습니다.
그래서 스마트폰 같은 소형 기기에도 쉽게 탑재될 수 있습니다. - 낮은 가격: 수정 발진기는 대량 생산이 가능하여, 고성능임에도 불구하고 저렴한 가격으로 제공될 수 있습니다.
이는 산업 전반에서 수정 발진기를 사용하는 주요 이유 중 하나입니다.
이러한 특성들 덕분에, 수정 발진기 원리는 다양한 분야에서 필수적인 기술로 자리 잡고 있습니다.
시계, 통신 시스템, 심지어 우리가 사용하는 컴퓨터의 CPU에도 수정 발진기가 사용됩니다.
- 연관 참조 : LC 발진기란?, 구성 요소, 공진 주파수 계산, 회로 설계 방법
- 연관 참조 : Hartley 발진기 원리, 동작, 주파수 계산, 예제, 장.단점
- 연관 참조 : Colpitts 발진기 원리, 동작, 발진 회로, 주파수 계산, 예제1, 장.단점
- 연관 참조 : RC 발진기 원리, TR을 사용한 기본회로, OP Amp을 사용한 회로, 예제1, 장.단점
- 연관 참조 : Wien 브릿지 발진기 원리,예제 풀이, 장.단점
2. 수정 발진기 원리
수정 발진기의 동작 원리를 이해하면, 왜 이 기술이 안정적인 주파수를 생성할 수 있는지 명확해집니다.
수정 발진기는 수정 크리스털의 물리적 특성을 기반으로 한 발진기입니다.
2-1) 등가 회로
수정 발진기를 설명할 때 가장 중요한 개념 중 하나는 등가 회로입니다.
수정 크리스털을 전기적으로 모델링한 회로를 보면, 그것은 사실상 하나의 LC 회로처럼 동작합니다.
수정 크리스털은 기계적 진동을 통해 전자 회로에서 주파수를 결정하는데, 이때 그 등가 회로는 인덕터(L), 커패시터(C), 저항(R)의 조합으로 표현됩니다.
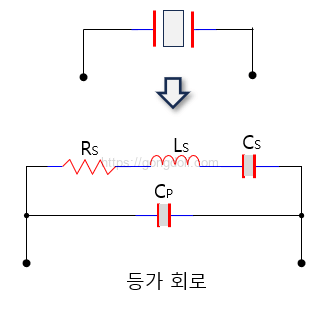
수정 크리스털의 등가 회로를 간단히 설명하면 다음과 같습니다.
- 저항(RS): 수정 크리스털의 기계적 손실을 나타냅니다.
즉, 크리스털이 진동하면서 생기는 약간의 에너지 손실을 의미합니다. - 인덕터(LS): 수정 크리스털의 질량에 해당하며, 진동하는 크리스털의 관성 효과를 나타냅니다.
- 커패시터(CS): 크리스털의 유연성 또는 저장된 전기 에너지를 나타냅니다.
- 병렬 커패시턴스 Cp는 크리스털의 전기적 연결부에서 발생하는 전기적 커패시턴스를 나타냅니다.
이는 크리스털의 기계적 특성과는 관련이 없으며, 크리스털이 외부 회로에 물리적으로 연결된 결과로 나타나는 값입니다.
이 회로는 수정 크리스털이 일정한 주파수로 진동하게 만드는데, 이때 수정 발진기 원리에 따라 안정적인 주파수가 생성됩니다.
2-2) 수정 발진기 원리
이제 수정 발진기 원리를 더 구체적으로 살펴보겠습니다.
수정 크리스털은 물리적으로 전압을 가했을 때 진동하는 성질을 갖고 있습니다.
이를 압전 효과라고 합니다.
수정 발진기는 이 압전 효과를 활용하여 매우 정밀한 주파수를 생성합니다.
수정 크리스털은 외부에서 전압을 가하면 특정 주파수로 진동을 시작합니다.
이 주파수는 수정 크리스털의 두께와 절단 각도에 따라 결정되는데, 수정의 물리적 특성 때문에 이 진동이 매우 일정하고 안정적입니다.
주파수 변화는 미세하고, 외부 환경(예: 온도 변화)에 거의 영향을 받지 않습니다.
가끔 “수정 발진기가 왜 정확한가요?”라는 질문을 하는 사람이 있습니다.
그 답은 바로 수정 크리스털의 독특한 물리적 특성에 있습니다.
수정 크리스털의 진동은 일정한 물리적 매개변수에 의해 통제되며, 전자회로와 연동하여 매우 정확한 주파수를 생성합니다.
이 때문에 수정 발진기는 시계나 통신 장비처럼 정확한 타이밍이 중요한 장치에서 필수적으로 사용됩니다.
예를 들어, 우리가 사용하는 손목시계나 스마트폰 속 수정 발진기는 32.768kHz라는 매우 정밀한 주파수를 생성합니다.
이 주파수를 통해 시간의 흐름을 정확하게 측정할 수 있는 것입니다.
그리고 이러한 원리가 수정 발진기 원리의 핵심입니다.
3. 주파수에 따른 크리스털의 임피던스
크리스털의 임피던스는 주파수에 따라 크게 변하는 특성을 가지고 있습니다.
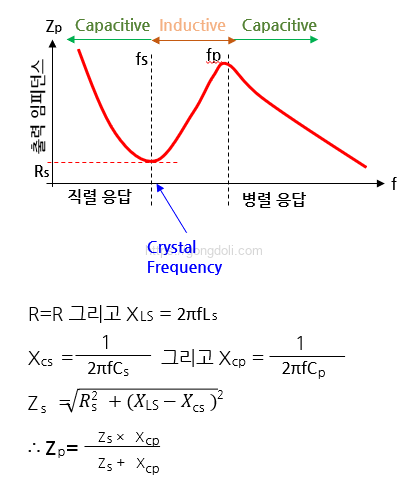
- 직렬 공진 주파수(ƒs)
주파수가 증가할 때, 크리스털은 처음에 커패시터 성질을 나타냅니다.
특정 주파수에서 Cs(직렬 커패시터)와 Ls(직렬 인덕터)의 상호작용으로 직렬 공진 회로가 형성됩니다.
이때 크리스털의 임피던스는 최소로 감소하며, Rs(직렬 저항)과 동일한 수준까지 떨어집니다.
이 지점을 직렬 공진 주파수(ƒs)라고 합니다.
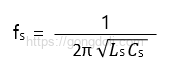
- 병렬 공진 주파수(ƒp)
주파수가 ƒs를 넘어 계속 상승하면, 크리스털은 인덕터 성질을 보이기 시작합니다.
주파수가 병렬 공진 주파수 ƒp에 도달할 때, Ls(직렬 인덕터)와 Cp(병렬 커패시터)의 상호작용으로 병렬 공진 회로가 형성됩니다.
이때 크리스털의 임피던스는 최대값에 도달하게 됩니다.
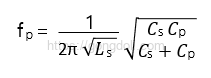
따라서 크리스털은 주파수에 따라 직렬 공진 주파수(ƒs)와 병렬 공진 주파수(ƒp)에서 각각 다른 동작을 하며, 직렬 및 병렬 공진 회로를 결합한 형태로 작동합니다.
3. 주파수에 따른 크리스털의 리액턴스
크리스털의 리액턴스는 주파수에 따라 매우 다른 양상을 보입니다.
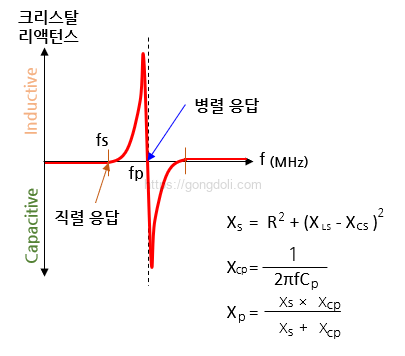
- 주파수 ƒs에서의 리액턴스 기울기
직렬 공진 주파수(ƒs)에서 크리스털의 직렬 리액턴스는 Cs(직렬 커패시턴스)에 반비례합니다.
즉, 주파수가 ƒs 아래에 있거나 ƒp 위에 있을 때 크리스털은 커패시터 성질을 나타냅니다.
- 주파수 ƒs와 ƒp 사이에서
ƒs와 ƒp 사이에서는 크리스털이 인덕터 성질을 띱니다.
이 주파수 구간에서 두 병렬 커패시턴스가 상쇄되어, 크리스털이 인덕터처럼 행동하게 됩니다.
3-1) 직렬,병렬 공진 주파수 예제
Rs = 6.4 ω, Cs = 0.09972pF 및 Ls = 2.546mH입니다.
단자 전체의 커패시턴스 Cp가 28.68pF로 측정되면 크리스털의 기본 진동 주파수와 2차 공진 주파수를 계산해보겠습니다.
먼저 직렬 공진 주파수(ƒs) 구해 보겠습니다.
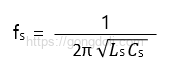
주어진 값
Ls=2.546mH=2.546×10−3H
Cs=0.09972pF=0.09972×10−12F
따라서, 직렬 공진 주파수(ƒs)는 약 9.988MHz입니다.
병렬 공진 주파수는 다음 공식으로 계산됩니다.
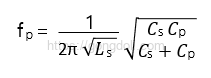
따라서, 병렬 공진 주파수(ƒp)는 약 10.006 MHz입니다.
두 공진 주파수 사이의 차이는 Δƒ = 10.006 MHz−9.988 MHz = 18 kHz
이 계산 결과는 직렬 공진 주파수와 병렬 공진 주파수 사이에 약 18kHz 차이가 발생함을 보여줍니다.
4. 크리스털의 Q-fackor
계산에서 보듯이 수정 발진기의 기본 주파수인 ƒs와 병렬 공진 주파수인 ƒp 사이의 차이는 약 18kHz로 매우 작습니다.
(10.005MHz – 9.987MHz).
그러나 이 주파수 범위에서는 수정 크리스털의 Q-팩터(품질 계수)가 매우 높습니다.
그 이유는 크리스털의 인덕턴스가 커패시턴스나 저항보다 훨씬 크기 때문입니다.
크리스털의 직렬 공진 주파수에서의 Q-팩터는 다음과 같이 정의됩니다.
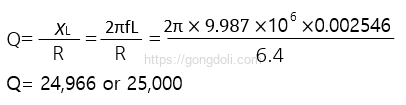
수정 발진기의 Q-팩터는 약 25,000으로 매우 높은데, 이는 수정 크리스털의 인덕턴스(XL)와 저항(R)의 비율이 높기 때문입니다.
대부분의 수정 발진기는 Q-팩터가 20,000에서 200,000 사이인 반면, 일반적인 LC 공진 회로의 Q-팩터는 1,000 이하인 경우가 많습니다.
이러한 높은 Q-팩터는 수정 발진기가 작동하는 주파수에서 더 높은 주파수 안정성을 제공하며, 발진기 회로에 이상적인 요소로 사용됩니다.
수정 발진기 원리에서 알 수 있듯이, 수정 크리스털은 전기적으로 조정된 LC 공진 회로와 유사한 공진 주파수를 가지고 있지만, 훨씬 높은 Q-팩터를 가집니다.
이는 주로 크리스털의 낮은 직렬 저항 Rs 덕분입니다.
그 결과, 수정 발진기는 특히 고주파 발진기에 매우 적합한 부품으로 선택됩니다.
일반적인 수정 발진기의 발진 주파수 범위는 약 40kHz에서 100MHz 이상으로, 회로 구성과 증폭 장치에 따라 달라질 수 있습니다.
또한, 크리스털의 절단 방식에 따라 수정이 여러 주파수에서 진동할 수 있으며, 이러한 진동은 ‘오버톤(overtones)’이라고 불리는 추가적인 발진을 생성합니다.
크리스털이 평행하거나 균일하지 않은 두께를 가지는 경우, 두 개 이상의 공진 주파수가 발생할 수 있습니다.
이 경우 기본 주파수 외에도 2차 또는 3차 고조파와 같은 여러 고조파가 생성될 수 있습니다.
그러나 일반적으로 수정 발진기의 기본 발진 주파수가 고조파보다 더 강력하게 나타나므로, 수정 발진기 원리에서 주로 기본 주파수가 사용됩니다.
수정 발진기 원리를 보면, 크리스털의 등가 회로는 세 가지 반응성 요소(두 개의 커패시터와 하나의 인덕터)를 가지며, 두 개의 공진 주파수가 존재합니다.
가장 낮은 것은 직렬 공진 주파수이고, 가장 높은 것은 병렬 공진 주파수입니다.
또한 발진기가 루프 이득이 1 이상이고 피드백이 양성인 경우, 증폭기 회로는 발진하게 됩니다.
수정 발진기 원리에서는 발진기가 크리스털의 기본 병렬 공진 주파수에서 발진하게 됩니다.
이는 전압이 적용되었을 때 크리스털이 항상 진동하려고 하기 때문입니다.
특정한 주파수에서 수정 발진기를 “조정”하여 기본 주파수의 짝수 고조파(2차, 4차, 8차 등)로 발진하도록 할 수 있으며, 이러한 발진기는 일반적으로 고조파 발진기라고 불립니다.
반면, ‘오버톤 발진기’는 기본 주파수의 홀수 배수(3차, 5차, 11차 등)에서 진동합니다.
일반적으로 오버톤 주파수에서 동작하는 수정 발진기는 직렬 공진 주파수를 사용하여 발진합니다.
5. Microprocessor의 수정 발진기
수정 발진기 원리에 대해 이야기하면서 마이크로프로세서 클록을 언급하지 않을 수 없습니다.
사실상 모든 마이크로프로세서, 마이크로컨트롤러, PIC, 그리고 CPU는 수정 발진기를 주파수 결정 장치로 사용하여 클록 파형을 생성합니다.
그 이유는 수정 발진기가 저항-커패시터(RC)나 인덕터-커패시터(LC) 발진기에 비해 가장 높은 정확도와 주파수 안정성을 제공하기 때문입니다.
CPU 클록은 프로세서의 작동 속도, 즉 데이터를 처리하는 속도를 결정합니다.
예를 들어, 클록 속도가 1MHz인 마이크로프로세서나 마이크로컨트롤러는 매 초당 100만 번의 클록 주기 동안 데이터를 처리할 수 있습니다.
수정 발진기 원리에 따라, 대부분의 마이크로프로세서 클록 파형을 생성하기 위해 필요한 것은 수정 크리스털과 15pF에서 33pF 범위의 두 개의 세라믹 커패시터뿐입니다.
다음과 같은 회로가 그 예시입니다.
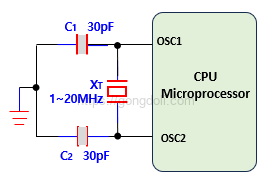
대부분의 마이크로프로세서, 마이크로컨트롤러, 그리고 PIC 칩에는 외부 수정 크리스털 회로나 표준 RC 발진기 네트워크, 또는 세라믹 공진자를 연결할 수 있는 두 개의 발진기 핀(OSC1, OSC2)이 있습니다.
이러한 마이크로프로세서 응용에서 수정 발진기는 연속적인 사각파 펄스열을 생성하며, 그 기본 주파수는 수정 발진기 자체가 결정합니다.
이 기본 주파수는 프로세서가 명령을 처리하고 시스템 타이밍을 조절하는 데 사용됩니다.
예를 들어, 수정 발진기 원리에 따르면 마스터 클록과 시스템 타이밍이 수정 발진기 회로에 의해 조정됩니다.
수정 발진기 회로는 안정적이고 정확한 주파수를 제공하기 때문에, 마이크로프로세서나 마이크로컨트롤러는 효율적으로 데이터를 처리할 수 있습니다.
수정 발진기 원리는 마이크로프로세서나 CPU에서 매우 중요한 역할을 합니다.
클록 신호의 정확성과 주파수 안정성은 프로세서가 데이터를 얼마나 신속하게 처리할 수 있는지를 결정하기 때문에, 수정 발진기 회로는 필수적인 요소입니다.