용량성 리액턴스, 원리, 예제 3개, 그래프

by

1. 용량성 리액턴스란?

용량성 리액턴스는 캐패시터가 전류를 통과하는데 제공하는 저항으로, 주파수에 따라 달라집니다.

우리는 AC와 DC 회로에서 캐패시터를 사용합니다.
그러나 AC와 DC에서 캐패시터의 행동은 다릅니다.
이는 왜냐하면 DC 주파수는 0이고 AC 주파수는 특정한 값이기 때문입니다.
이에 따라 캐패시터의 리액턴스도 두 경우에 따라 다릅니다.

캐패시터에 DC 전압을 가하면, 캐패시터는 충전 전류를 끌어들이고 공급 전압까지 충전됩니다.
공급 전압이 감소하면 캐패시터가 방전되고 캐패시터 전압이 감소합니다.

캐패시터에 AC 전압을 가하면, 캐패시터 전압은 일정하지 않고, 한 주기에서는 양수이고, 다음 주기에서는 음수가 됩니다.
이러한 조건에서 캐패시터는 공급 주파수에 따라 지속적으로 충전 및 방전됩니다.

한 주기의 양수 반주기에서는 캐패시터가 충전되고, 다음 반주기에서는 캐패시터가 저장된 에너지를 소스로 다시 피드백합니다. 따라서 완전한 주기 동안 캐패시터에 의해 소비되는 전력은 제로입니다.

캐패시터의 내부 임피던스는 충전 및 방전 전류를 제한합니다.
이 내부 임피던스는 캐패시터의 리액턴스이며, 기호로 XC로 표시합니다. 그 단위는 Ω입니다.

2. 용량성 리액턴스 원리

캐패시터 동작 원리는 캐패시터는 전기적으로 이중층으로 이루어진 구조를 가지고 있습니다.
이중층은 양극과 음극으로 이루어져 있으며, 양극에는 양의 전하가, 음극에는 음의 전하가 축적됩니다.
캐패시터는 이렇게 축적된 전하를 저장하고, 전류의 흐름을 허용합니다.

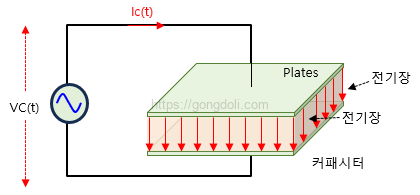
용량성 리액턴스

주파수에 따른 캐패시터의 행동: 용량성 리액턴스는 주로 AC 회로에서 중요한데, 이는 AC 전압이 주기적으로 변화하면서 캐패시터가 반복적으로 충전 및 방전되기 때문입니다.
주파수가 증가하면 캐패시터가 빠르게 충전 및 방전되는데, 이 때문에 용량성 리액턴스는 주파수의 증가에 따라 감소합니다.

저장된 에너지와 전류 흐름: 캐패시터는 전하를 축적하여 에너지를 저장합니다.
주파수가 낮은 AC 신호에서는 캐패시터가 전하를 더 많이 축적하고, 따라서 더 많은 에너지를 저장합니다.
또한, 주파수가 증가하면 캐패시터가 전류를 더 쉽게 허용하게 되어, 높은 주파수에서는 더 많은 전류가 흐릅니다.

AC와 DC 회로의 차이는 DC 회로에서는 캐패시터는 초기에만 충전되거나 방전됩니다.
이에 따라 초기에는 매우 높은 전류가 흐르지만, 시간이 지나면 전류는 줄어들어 최종적으로는 0이 됩니다.
반면에 AC 회로에서는 주기적으로 캐패시터가 충전 및 방전되므로, 계속해서 전류가 흐릅니다.

이러한 원리를 이해하면 capacitive reactance가 전기 회로에서 어떻게 작용하는지 더 잘 이해할 수 있습니다.

3. 용량성 리액턴스 계산 방법 및 예제

3-1) 공식

리액턴스와 주파수 관계는 용량성 리액턴스는 주파수와 반비례 관계에 있습니다.
수식적으로는

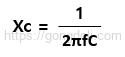
용량성 리액턴스 : 수식
  • 여기서
  • XC는 용량성 reactance (단위: 옴, Ω)
  • f는 적용된 주파수 (단위: 헤르츠, Hz)
  • C는 캐패시터의 용량 (단위: 패럿, F)
  • XC는 용량성 reactance (단위: 옴, Ω)
  • f는 적용된 주파수 (단위: 헤르츠, Hz)
  • C는 캐패시터의 용량 (단위: 패럿, F)
커패시터 리액턴스 계산기

3-2) 예제 1

1kHz 주파수에서 220nF 캐패시터의 용량 리액턴스 값을 계산하고 다시 20kHz 주파수 일 때를 계산해 보겠습니다.

캐패시터의 용량성 리액턴스를 계산한 공식을 사용하면

XC = 1 / (2πfC)

주어진 값은

  • 용량 (C) = 220nF = 220×10−9 F
  • 주파수 (f)
    • 첫 번째, 1kHz에서 = 1000 Hz
    • 두 번째, 20kHz에서 = 20000 Hz

1 KHz일 때

XC = 1 / (2πfC) = 1 / (2π×1000×220×10−9)​ ≈ 723.43Ω

20 KHz일 때

XC = 1 / (2πfC) = 1 / (2π×20000×220×10−9)​ ≈ 36.17Ω

따라서, 220nF 캐패시터의 1kHz에서의 용량성 reactance는 약 723.43Ω이고, 20kHz에서의 용량성 reactance는 약 36.17Ω입니다.

4. 용량성 리액턴스 그래프 및 예제

4-1) 용량성 리액턴스 그래프

위에 식으로부터 주파수(f)가 증가함에 따라 용량성 리액턴스(XC)가 감소하는 것을 알 수 있습니다.
반대로, 주파수가 감소함에 따라 용량성 리액턴스는 증가합니다.

이 관계는 용량성 reactance가 주파수의 지수적으로 증가하거나 감소하는 곡선으로 그래픽적으로 나타납니다.
낮은 주파수에서는 용량성 리액턴스가 높아져 캐패시터를 통한 전류 흐름이 제한됩니다.
주파수가 증가함에 따라 용량성 reactance는 감소하여 더 많은 전류가 캐패시터를 통과할 수 있게 됩니다.

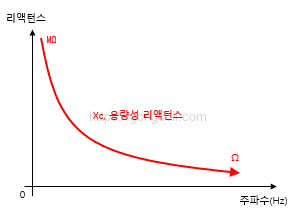
용량성 리액턴스 : 그래프

요약하면, 주파수에 대한 용량성 reactance는 높은 주파수일수록 리액턴스가 낮아지고, 낮은 주파수일수록 리액턴스가 높아지는 반비례 관계를 보입니다.

4-2) 예제 2

2.2μF 캐패시터의 리액턴스 값이 200Ω이라고 할 때, 파수f)를 구해 보겠습니다.

용량성 reactance에 대한 공식은

XC = 1 / (2πfC)

주파수 (f)를 구하기 위해 공식을 다음과 같이 풀면

f = 1 / (2πXC​C1)

주어진 값

  • XC​=200Ω
  • C=2.2μF=2.2×10−6 F

즉,

f = 1 / (2πXC​C) = 1 / (2π×200×2.2×10−6) ≈ 360.66Hz

따라서, 2.2μF 캐패시터는 약 360.66 Hz의 주파수에서 200Ω의 리액턴스 값을 갖게 됩니다.

4-3) 예제 3

용량 리액턴스가 200 ω이고 50Hz 공급 장치에 연결되어 있을 때 패러드에서 캐패시터의 값은 얼마인지 계산해 보겠습니다.

용량성 reactance에 대한 공식은

XC = 1 / (2πfC)

캐패시터의 값 (C)을 구하기 위해 공식을 다음과 같이 풀면

C= 1/(2πfXC​)

주어진 값은

  • XC​=200Ω
  • f=50 Hz

즉,

C= 1/(2πfXC​) = 1/ (2π×50×200) = ≈1.592×10−5F

따라서, 용량성 reactance가 200Ω이고 50Hz 공급에 연결된 경우 캐패시터의 값은 약 1.592×10−5F(15.92uF)입니다

5. 용량성 리액턴스 요약 및 활용

낮은 주파수에서의 높은 용량성 리액턴스: 매우 낮은 주파수에서는 캐패시터의 용량성 리액턴스가 매우 높습니다.
이는 캐패시터가 실질적으로 회로를 열고 전류 흐름을 차단하는 역할을 합니다.
이 때문에 낮은 주파수에서는 캐패시터는 거의 통과할 수 없는 장벽처럼 작동합니다.

높은 주파수에서의 낮은 용량성 리액턴스는 반면에 매우 높은 주파수에서는 캐패시터의 용량성 리액턴스가 낮아집니다.
이는 캐패시터가 실질적으로 회로에 짧은 회로를 형성하고 전류가 쉽게 흐를 수 있도록 합니다.
따라서 높은 주파수에서는 캐패시터는 전류를 자유롭게 흐르게 할 수 있습니다.

주파수가 용량에 미치는 영향은 캐패시터가 전기 회로에서 어떻게 작동하는지 이해하는 데 중요합니다.
이러한 특성은 다양한 회로 및 장치에서 캐패시터의 사용을 제어하고 설계하는 데 중요한 역할을 합니다.

예를 들어, 용량성 리액턴스를 활용하는 일반적인 예로는 필터 회로가 있습니다.
필터는 전기 회로에서 특정 주파수의 신호를 차단하거나 통과시키는 데 사용됩니다.
용량성 리액턴스는 필터 회로에서 중요한 구성 요소로 작용할 수 있습니다.

  • 로우 패스 필터 (Low Pass Filter): 로우 패스 필터는 저주파 신호를 통과시키고 고주파 신호를 차단하는 데 사용됩니다.
    이 필터에서는 캐패시터가 주요 구성 요소로 사용되며, 이 캐패시터의 용량성 리액턴스는 낮은 주파수에서는 높고 고주파에서는 낮기 때문에 저주파 신호를 쉽게 통과시키고 고주파 신호를 차단할 수 있습니다.
  • 하이 패스 필터 (High Pass Filter): 하이 패스 필터는 고주파 신호를 통과시키고 저주파 신호를 차단하는 데 사용됩니다.
    이 필터에서도 캐패시터가 주요 구성 요소이며, 낮은 주파수에서는 용량성 리액턴스가 높고 고주파에서는 낮아서 고주파 신호를 통과시키고 저주파 신호를 차단합니다.
  • 밴드 패스 필터 (Band Pass Filter): 밴드 패스 필터는 특정 주파수 범위 내의 신호를 통과시키는 데 사용됩니다.
    이 필터는 로우 패스 필터와 하이 패스 필터를 결합하여 구성될 수 있으며, 이 과정에서 캐패시터의 용량성 리액턴스가 중요한 역할을 합니다.

이러한 필터 회로에서 용량성 리액턴스를 적절히 선택하고 조절함으로써 원하는 주파수 범위의 신호를 선택적으로 통과시키거나 차단할 수 있습니다.
이를 통해 특정 응용 분야에 맞는 필터를 설계하고 구현할 수 있습니다.

Leave a Comment

error: Content is protected !!