Contents
1. 이진수란 무엇인가?
이진수(Binary)는 숫자를 0과 1, 두 가지 숫자만을 사용해 표현하는 숫자 체계입니다.
이진법이라고도 불리는 이 숫자 체계는 컴퓨터와 디지털 시스템에서 정보를 처리하고 저장하는 기본적인 방식입니다.
우리 일상에서 흔히 사용하는 10진수는 0부터 9까지의 숫자를 사용하지만, 이진수는 0과 1만을 사용합니다.
이진수(Binary)의 개념은 현대 컴퓨터 과학과 전자공학의 기초가 되는 중요한 이론입니다.
이진법의 기원은 고대 중국의 철학에서 찾아볼 수 있습니다.
기원전 9세기경의 주역(周易)에는 64개의 서로 다른 괘(卦)가 있는데, 이 괘는 음(陰)과 양(陽)으로 이루어진 이진 패턴으로 해석될 수 있습니다.
18세기 독일의 수학자이자 철학자인 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)는 이진법을 체계적으로 연구하였습니다.
그는 1703년에 발표한 논문 “Explication de l’Arithmétique Binaire”에서 이진법을 소개하며, 이를 주역의 괘와 연결지었습니다.
라이프니츠는 이진법이 수학적 계산뿐만 아니라 논리적 사고와 철학적 개념을 표현하는 데 유용하다고 주장했습니다.
이진법이 현대적 의미를 갖게 된 것은 20세기 중반에 들어서면서부터입니다.
특히, 컴퓨터 과학의 아버지로 불리는 앨런 튜링(Alan Turing)과 클로드 섀넌(Claude Shannon)이 이진수를 사용하여 컴퓨터와 디지털 시스템의 설계와 이론을 발전시켰습니다.
튜링은 컴퓨터가 논리적 연산을 수행하는 데 이진수(Binary)를 사용할 수 있음을 보였고, 섀넌은 디지털 회로에서 이진수(Binary)를 사용하여 정보를 처리하는 방식을 개발하였습니다.
오늘날 이진수(Binary)는 모든 컴퓨터 시스템의 핵심입니다.
컴퓨터는 전기 신호를 통해 정보를 처리하는데, 이때 전기 신호는 켜짐(1)과 꺼짐(0)의 두 가지 상태만 가질 수 있습니다.
이진수(Binary)는 이러한 이진 상태를 표현하기에 적합한 체계로, 컴퓨터의 메모리, 프로세서, 저장 장치 등 모든 부품에서 사용됩니다.
- 연관 참조 : 16진수 (hexadecimal),표기법과 구조,16진수↔10진수/2진수 변환 예제,16진수연산
- 연관 참조 : 8진수_octal, 십진수 & 2진수로 변환, 8진수 연산,예제
- 연관 참조 : 16진수 사칙 연산 계산기, hexadecimal calculator, 사용 방법
- 연관 참조 : 8진수 사칙 연산 계산기, Hexadecimal calculator, 사용 방법
2. 이진수(Binary) 표기법과 구조
2-1) 이진수의 기본 구조
이진수(Binary)는 두 가지 숫자, 즉 0과 1만을 사용하여 숫자를 표현합니다.
이진수는 2진법(Binary System)에 기반을 두고 있으며, 각 자리는 2의 거듭제곱을 나타냅니다.
오른쪽에서 왼쪽으로 갈수록 자릿수의 값이 증가하며, 각각의 자리는 0 또는 1의 값을 가집니다.
예를 들어, 이진수 1101은 다음과 같이 계산해 보겠습니다.
첫 번째 자리(오른쪽 끝): 1 × 20 = 1
두 번째 자리: 0 × 21 = 0
세 번째 자리: 1 × 22 = 4
네 번째 자리: 1 × 23 = 8
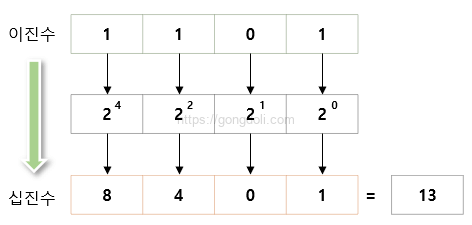
이 값을 모두 더하면
8 + 4 + 0 + 1 = 13 (십진수)
따라서, 이진수 1101은 십진수로 13을 의미합니다.
2-2) 이진수와 십진수의 차이점
십진수는 0부터 9까지의 숫자를 사용하여 수를 표현하며, 10진법(Decimal System)에 기반을 둡니다.
각 자리는 10의 거듭제곱을 나타냅니다.
예를 들어, 숫자 345는 다음과 같이 계산됩니다.
첫 번째 자리(오른쪽 끝): 5 × 100 = 5
두 번째 자리: 4 × 101 = 40
세 번째 자리: 3 × 102 = 300
이 값을 모두 더하면
300 + 40 + 5 = 345 (십진수)
이진수(Binary)와 십진수의 주요 차이점은 다음과 같습니다.
- 기수(Base): 이진수는 2를 기수로 사용하고, 십진수는 10을 기수로 사용합니다.
- 자리의 값: 이진수에서는 각 자리가 2의 거듭제곱을 나타내고, 십진수에서는 각 자리가 10의 거듭제곱을 나타냅니다.
- 사용하는 숫자: 이진수는 0과 1만을 사용하며, 십진수는 0부터 9까지의 숫자를 사용합니다.
2-3) 이진수의 기호 및 표기 방식
이진수(Binary)는 0과 1로 이루어진 숫자들의 나열로 표기됩니다.
이진수를 명확하게 구분하기 위해 ‘b’나 ‘B’를 붙여 표기하거나, ‘0b’ 또는 ‘0B’를 접두사로 붙이는 경우가 많습니다.
이는 특히 프로그래밍 언어에서 자주 사용됩니다.
예를 들어
이진수 1010은 십진수로 10입니다.
이를 명확히 구분하기 위해 1010b 또는 0b1010으로 표기할 수 있습니다.
프로그래밍 언어에서의 예시
Python에서 이진수(Binary)를 나타낼 때는 접두사 ‘0b’를 사용합니다. 예: 0b1010
C 언어에서는 접두사 ‘0b’를 사용하지 않지만, 주석으로 설명할 수 있습니다. 예: 1010 /* binary */
이진수의 각 자리는 비트(bit)라고 불리며, 8개의 비트가 모여 1바이트(byte)를 구성합니다.
각 비트는 0 또는 1의 값을 가지며, 컴퓨터에서 데이터를 표현하고 저장하는 기본 단위입니다.
예를 들어
8비트 이진수 11001010은 다음과 같은 값을 가집니다.
1 × 27 = 128
1 × 26 = 64
0 × 25 = 0
0 × 24 = 0
1 × 23 = 8
0 × 22 = 0
1 × 21 = 2
0 × 20 = 0
이 값을 모두 더하면
128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202 (십진수)
이진수(Binary)는 이러한 비트들의 조합으로 다양한 숫자와 정보를 표현하며, 컴퓨터와 디지털 시스템에서 필수적인 역할을 합니다.
3. 이진수(Binary)을 십진수로 변환 방법
3-1) 십진수를 이진수로 변환하는 방법
십진수를 이진수(Binary)로 변환하는 방법은 크게 두 가지가 있습니다.
나눗셈을 사용하는 방법과 재귀적인 방법입니다.
여기에서는 나눗셈을 사용하는 방법을 중점적으로 설명하겠습니다.
3-1-1) 나눗셈을 사용한 변환 방법
십진수를 2로 나눕니다.
나머지를 기록합니다.
몫을 다시 2로 나눕니다.
이 과정을 몫이 0이 될 때까지 반복합니다.
기록된 나머지들을 역순으로 나열합니다.
3-1-2) 예시: 십진수 19를 이진수로 변환해 보겠습니다.
- 19 ÷ 2 = 9, 나머지 1
- 9 ÷ 2 = 4, 나머지 1
- 4 ÷ 2 = 2, 나머지 0
- 2 ÷ 2 = 1, 나머지 0
- 1 ÷ 2 = 0, 나머지 1
- 기록된 나머지: 1, 1, 0, 0, 1
이진수로 변환된 값: 10011
따라서, 십진수 19는 이진수 10011로 변환됩니다.
3-2) 이진수를 십진수로 변환하는 방법
이진수를 십진수로 변환하는 방법은 이진수(Binary)의 각 자리수에 2의 거듭제곱을 곱한 후, 이를 모두 더하는 방식입니다.
이진수의 각 자리수를 확인합니다.
각 자리수에 해당 자리의 2의 거듭제곱을 곱합니다.
모든 곱셈 결과를 더합니다.
예시: 이진수 1011을 십진수로 변환해 보겠습니다.
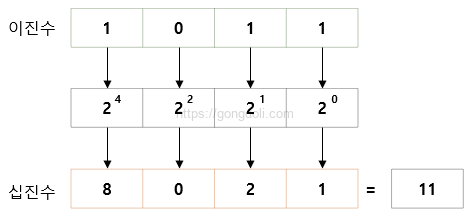
오른쪽 첫 번째 자리: 1 × 20 = 1
두 번째 자리: 1 × 21 = 2
세 번째 자리: 0 × 22 = 0
네 번째 자리: 1 × 23 = 8
이 값을 모두 더하면
1 + 2 + 0 + 8 = 11
따라서, 이진수 1011은 십진수 11로 변환됩니다.
3-3) 이진수 변환의 실생활 응용
이진수 변환은 컴퓨터 과학과 디지털 시스템에서 매우 중요한 역할을 합니다.
3-3-1) 컴퓨터 프로그래밍
컴퓨터의 모든 데이터는 이진수(Binary)로 저장되고 처리됩니다.
텍스트 파일, 이미지, 비디오 등 모든 데이터는 내부적으로 이진수 형태로 저장됩니다.
프로그래밍 언어에서 숫자를 이진수로 변환하는 기능은 가장 흔히 사용됩니다.
예를 들어, Python에서는 bin() 함수를 사용하여 십진수를 이진수로 변환할 수 있습니다.
3-3-2) 디지털 회로 설계
디지털 회로는 논리 게이트로 구성되며, 이진수를 사용하여 입력과 출력을 처리합니다.
예를 들어, AND, OR, NOT 게이트는 각각의 입력을 이진수로 처리하여 결과를 산출합니다.
마이크로프로세서는 명령어를 이진수로 해석하고 실행합니다.
이는 컴퓨터가 명령을 이해하고 수행하는 기본적인 방식입니다.
3-3-3) 네트워크와 통신
네트워크 주소(IP 주소)는 이진수(Binary)로 표현됩니다.
IPv4 주소는 32비트 이진수로 구성되며, 이는 네트워크 상에서의 장치 식별에 사용됩니다.
데이터 전송은 이진수를 사용하여 이루어집니다.
예를 들어, 인터넷을 통해 전송되는 모든 데이터 패킷은 이진수 형태로 인코딩되어 전송됩니다.
3-3-4) 디지털 이미지와 비디오
디지털 이미지와 비디오는 픽셀 단위로 저장되며, 각 픽셀의 색상 정보는 이진수(Binary)로 표현됩니다.
예를 들어, 8비트 그레이스케일 이미지는 각 픽셀이 0부터 255까지의 값을 가지며, 이는 8비트 이진수(Binary)로 저장됩니다.
비디오 압축 기술에서도 이진수를 사용하여 데이터를 효율적으로 저장하고 전송합니다.
이와 같이 이진수 변환은 컴퓨터와 디지털 시스템에서 중요한 역할을 하며, 다양한 실생활 응용에서 필수적인 기술입니다.
4. 이진수(Binary) 연산
이진수는 0과 1만을 사용하여 수를 표현하기 때문에, 이진수(Binary) 간의 연산은 십진수 연산과는 다른 규칙을 따릅니다.
이진수(Binary) 덧셈, 뺄셈, 곱셈, 나눗셈을 차례로 설명하겠습니다.
4-1) 이진수 덧셈
이진수(Binary) 덧셈은 십진수 덧셈과 유사하지만, 0과 1만을 사용합니다.
두 이진수를 더할 때 자리올림(Carry)이 발생할 수 있습니다.
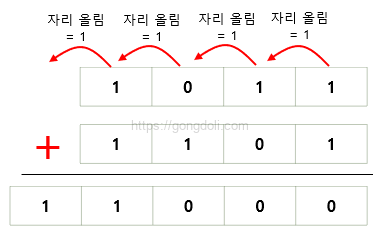
기본 규칙
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (자리올림 1)
예시: 1011 + 1101을 계산해 보겠습니다.
덧셈 과정을 단계별로 보면
오른쪽 첫 번째 자리: 1 + 1 = 0 (자리올림 1)
두 번째 자리: 1 + 0 + 1(자리올림) = 0 (자리올림 1)
세 번째 자리: 0 + 1 + 1(자리올림) = 0 (자리올림 1)
네 번째 자리: 1 + 1 + 1(자리올림) = 1 (자리올림 1)
마지막 자리: 1(자리올림)
결과는 11000입니다.
4-2) 이진수 뺄셈
이진수(Binary) 뺄셈은 십진수 뺄셈과 유사하지만, 0에서 1을 빼는 경우 자리내림(Borrow)이 발생합니다.
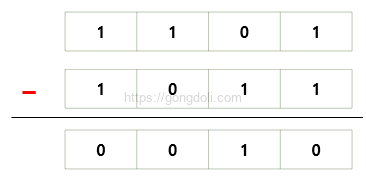
기본 규칙
- 0 – 0 = 0
- 1 – 0 = 1
- 1 – 1 = 0
- 0 – 1 = 1 (자리내림 1)
예시: 1101 – 1011을 계산해 보겠습니다.
뺄셈 과정을 단계별로 보면
- 오른쪽 첫 번째 자리: 1 – 1 = 0
- 두 번째 자리: 0 – 1 = 1 (자리내림 1)
- 세 번째 자리: 1 – 0 – 1(자리내림) = 0
- 네 번째 자리: 1 – 1 = 0
결과는 0010입니다.
4-3) 이진수 곱셈
이진수(Binary) 곱셈은 십진수 곱셈과 유사하지만, 각 자리의 곱셈 결과를 더하여 최종 결과를 얻습니다.
이진수의 곱셈은 주로 자리 이동과 덧셈으로 이루어집니다.
기본 규칙:
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
예시: 101 × 11을 계산해 보겠습니다.
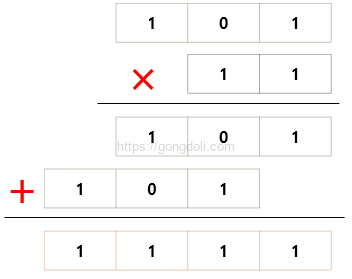
곱셈 과정을 단계별로 보면
- 첫 번째 자리: 101 × 1 = 101
- 두 번째 자리: 101 × 1 = 101 (한 자리 왼쪽으로 이동)
- 두 결과를 더하면: 101 + 1010 = 1111
결과는 1111입니다.
4-4) 이진수 나눗셈
이진수(Binary) 나눗셈은 십진수 나눗셈과 유사하지만, 이진수를 사용합니다. 나눗셈 과정은 나머지와 몫을 계산하는 단계로 이루어집니다.
예시: 11010 ÷ 11을 계산해 보겠습니다.
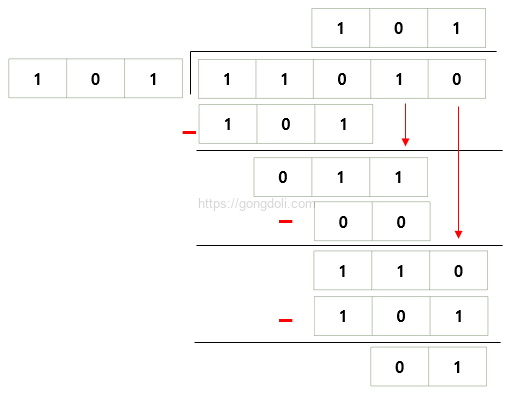
나눗셈 과정을 단계별로 보면
- 첫 번째 자리 비교: 110 >= 101, 몫 1, 나머지 011
- 나머지에 다음 자리 추가: 0110
- 네 번째 자리 비교: 0110 >= 101, 몫 1, 나머지 001
- 나머지에 다음 자리 추가: 0100
- 다섯 번째 자리 비교: 0100 < 101, 몫 0
최종 결과는 몫: 101, 나머지: 1입니다.
5. 이진수(Binary)와 컴퓨터
5-1) 컴퓨터 내부의 데이터 표현
컴퓨터는 모든 데이터를 0과 1로 이루어진 이진수 형태로 처리합니다.
이는 전자 회로가 두 가지 상태(전압이 있거나 없는 상태)를 구별할 수 있기 때문입니다.
이를 통해 컴퓨터는 다양한 데이터를 처리할 수 있습니다.
예를 들어, 숫자, 문자, 이미지, 소리 등 모든 형태의 데이터는 이진수로 변환되어 컴퓨터 내부에서 저장되고 처리됩니다.
- 숫자: 10진수 5는 이진수로 101입니다.
- 문자: 문자 ‘A’는 아스키 코드에서 10진수로 65, 이진수로는 01000001입니다.
- 이미지: 이미지는 픽셀 단위로 RGB 색상 값을 이진수로 표현하여 저장합니다.
5-2) 메모리와 이진수
컴퓨터 메모리는 데이터를 저장하는 역할을 합니다.
메모리는 여러 개의 셀로 구성되어 있으며, 각 셀은 0 또는 1을 저장할 수 있는 비트로 이루어져 있습니다.
메모리 셀들은 주소를 통해 구분되며, 각 주소에는 특정한 데이터가 저장됩니다.
- 바이트: 8비트가 모여 하나의 바이트를 구성합니다.
한 바이트는 256(2^8)가지의 값을 표현할 수 있습니다. - 메모리 주소: 메모리의 각 바이트는 고유의 주소를 갖습니다.
예를 들어, 주소 1000번지에 01010101이라는 이진수가 저장될 수 있습니다.
만약, “Hello”라는 문자열을 메모리에 저장하는 경우, 각 문자는 아스키 코드로 변환되고, 해당 이진수 값이 메모리의 연속된 주소에 저장됩니다.
5-3) 컴퓨터 명령어와 이진수
컴퓨터는 중앙처리장치(CPU)가 명령어를 실행하여 작업을 수행합니다.
이 명령어들도 이진수로 표현됩니다.
각 명령어는 특정 작업을 수행하도록 CPU에 지시합니다.
명령어는 크게 연산 명령어, 데이터 전송 명령어, 분기 명령어 등으로 나눌 수 있습니다.
- 연산 명령어: 두 숫자를 더하거나 곱하는 명령어.
예를 들어, 0001 1010은 두 숫자를 더하는 명령어일 수 있습니다. - 데이터 전송 명령어: 데이터를 특정 위치로 이동시키는 명령어.
예를 들어, 0010 0101은 데이터를 레지스터에서 메모리로 이동시키는 명령어일 수 있습니다. - 분기 명령어: 프로그램 실행 흐름을 변경하는 명령어.
예를 들어, 0100 1100은 특정 조건이 충족될 때 프로그램의 실행을 다른 위치로 이동시키는 명령어일 수 있습니다.
이러한 명령어들은 CPU의 제어 유닛에 의해 해석되어 실행됩니다.
만약, 어떤 프로그램이 “2 더하기 3″을 계산하는 경우, CPU는 이 작업을 수행하기 위한 일련의 명령어들을 이진수로 처리하여 계산 결과를 메모리에 저장하거나 출력 장치로 보냅니다.