Contents
1. 이진 가산기란?
이진 가산기 회로 설계는 두 개의 이진수를 더하는 디지털 회로를 설계하는 과정입니다.
이진 가산기는 디지털 시스템에서 중요한 구성 요소로, 0과 1로 이루어진 이진수를 더하는 연산을 수행합니다.
이진 가산기 회로 설계의 기본 개념에는 두 가지 주요 유형이 있습니다.
- 반가산기(Half Adder) : 두 개의 단일 비트 이진수를 더하는 회로입니다.
결과로는 합(Sum)과 자리올림(Carry) 값이 생성됩니다.
예를 들어, 1과 1을 더하면 합은 0이고, 자리올림은 1입니다. - 전가산기(Full Adder) : 두 개의 단일 비트 이진수와 이전 자리올림 값을 더하는 회로입니다.
결과로는 합과 새로운 자리올림 값이 생성됩니다.
전가산기는 반가산기 두 개와 추가 논리 게이트로 구성됩니다.
이진 가산기 회로 설계의 주요 기능은 다음과 같습니다.
- 이진수 덧셈 : 이진 가산기 회로 설계의 기본 기능은 두 개의 이진수를 더하는 것입니다.
이는 컴퓨터와 디지털 시스템에서 필수적인 연산입니다. - 자리올림 처리 : 덧셈 결과가 2를 초과할 경우, 자리올림 값을 생성하여 다음 자리로 전달합니다.
이는 여러 비트를 포함하는 이진수의 덧셈에서 중요한 역할을 합니다. - 병렬 덧셈 : 여러 비트의 이진수를 동시에 처리할 수 있도록 다중 비트 가산기를 구성할 수 있습니다.
이는 빠르고 효율적인 덧셈 연산을 가능하게 합니다.
- 연관 참조 : 이진 감산기 회로 설계, 직렬과 병렬 감산기 비교, 회로 설계 예제 3가지
- 연관 참조 : 비교기 회로 설계, 유형, 회로 설계 방법, 예제, 주의 사항 7가지
- 연관 참조 : 2진 디코더 회로 설계, 회로 설계 방법, 예제,설계 문제 4가지
- 연관 참조 : Encoder 회로 설계, 회로 설계 방법, 예제, 흔한 설계 문제 4가지
- 연관 참조 : Demultiplexer 회로 설계, 회로 설계 방법, 예제, 흔한 설계 문제 5가지
- 연관 참조 : Multiplexer 회로 설계,유형과 종류,회로 설계 방법, 예제
- 연관 참조 : 조합 논리 회로, 회로 설계, 부울 대수 이용, 카르노 맵 이용,예제1
2. 이진 가산기 회로 설계 방법
2-1) 기본 설계 원리: 진리표에서 논리식으로
이진 가산기 회로 설계의 첫 번째 단계는 진리표를 작성하고 이를 기반으로 논리식을 도출하는 것입니다.
진리표는 모든 가능한 입력 조합에 대한 출력을 보여주는 표입니다.
반가산기와 전가산기의 진리표를 통해 논리식을 도출할 수 있습니다.
예를 들어, 반가산기의 진리표는 다음과 같습니다.
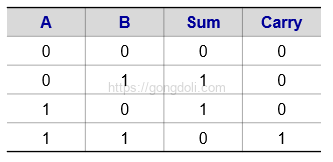
이 진리표에서 합(S)과 자리올림(C)의 논리식을 도출할 수 있습니다.
- Sum = A XOR B
- Carry = A AND B
2-2) 반가산기 설계
이진 가산기 회로 설계에서 반가산기 설계는 앞서 도출한 논리식을 기반으로 합니다.
반가산기는 두 개의 입력(A, B)과 두 개의 출력(합 S, 자리올림 C)으로 구성됩니다
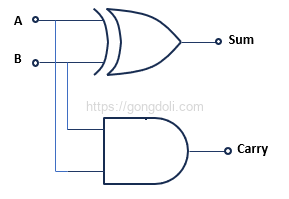
반가산기 회로 설계의 구성 요소
- XOR 게이트: 합(S) 출력
- AND 게이트: 자리올림(C) 출력
2-3) 전가산기 설계
이진 가산기 회로 설계에서 전가산기 설계는 반가산기를 두 번 사용하여 이루어집니다.
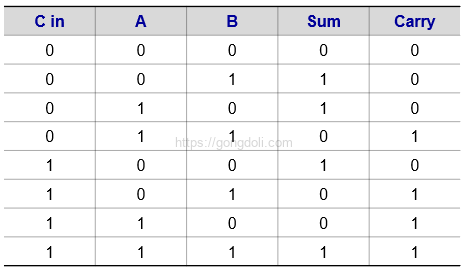
전가산기는 세 개의 입력(A, B, 이전 자리올림 Cin)과 두 개의 출력(합 S, 새로운 자리올림 Carry)으로 구성됩니다.
전가산기 회로 설계의 단계
- 첫 번째 반가산기 : A와 B를 입력하여 첫 번째 합(S1)과 첫 번째 자리올림(C1)을 얻습니다.
- 두 번째 반가산기 : S1과 Cin을 입력하여 최종 합(S)을 얻습니다.
- OR 게이트 : C1과 두 번째 반가산기의 자리올림을 OR 게이트에 입력하여 최종 자리올림(Carry)을 얻습니다.
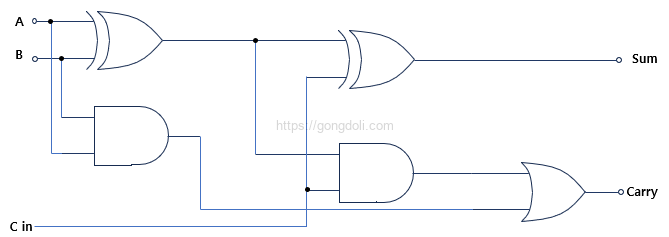
논리식
Sum = (A XOR B) XOR Cin
Carry = (A AND B) OR (Cin AND (A XOR B))
2-4) 다중 비트 가산기의 설계와 최적화
이진 가산기 회로 설계에서 다중 비트 가산기 회로 설계는 여러 개의 전가산기를 병렬로 연결하여 이루어집니다.
n-비트 가산기는 n개의 전가산기로 구성되며, 각 전가산기의 출력 자리올림은 다음 전가산기의 입력 자리올림으로 사용됩니다.
예를 들어, 4비트 가산기의 회로 설계는 다음과 같습니다.
- 4개의 전가산기를 사용하여 각 비트를 더합니다.
- 첫 번째 전가산기의 Cin은 0으로 설정합니다.
- 각 전가산기의 Cout은 다음 전가산기의 Cin으로 입력됩니다.
최적화 기법
- 캐리 룩어헤드 가산기(Carry Lookahead Adder) : 캐리 신호를 병렬로 계산하여 가산 속도를 향상시킵니다.
- 리플 캐리 가산기(Ripple Carry Adder) : 간단하지만 캐리 전파로 인해 속도가 느립니다.
- 캐리 저장 가산기(Carry Save Adder) : 여러 가산기를 병렬로 사용하여 연산 속도를 높입니다.
3. 이진 가산기 회로 설계 예제
3-1) 2비트 전가산기 회로 설계 단계별 설명
이진 가산기 회로 설계에서 2비트 전가산기는 두 개의 2비트 이진수를 더하는 회로입니다.
이는 기본적으로 두 개의 1비트 전가산기를 사용하여 설계할 수 있습니다.
각 비트의 합과 자리올림을 계산하는 단계로 구성됩니다.
1단계 : 진리표 작성
2비트 전가산기의 진리표는 각 비트에 대해 작성합니다.
여기서 A와 B는 2비트 입력, Cin은 입력 캐리, S는 합, Cout는 출력 캐리입니다.
-. 입력과 출력 변수
- A = A1A0 (2비트 입력)
- B = B1B0 (2비트 입력)
- Cin (입력 캐리)
- S = S1S0 (2비트 합)
- Cout (출력 캐리)
-. 1비트 전가산기 진리표
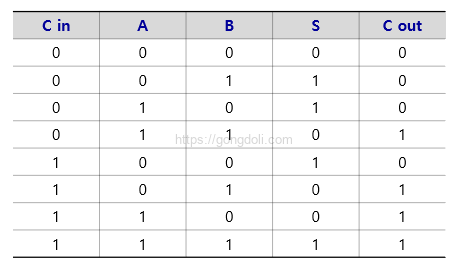
2비트 전가산기의 경우, 각 비트의 전가산기를 개별적으로 설계하여 연결합니다.
2단계 : 논리식 도출
1비트 전가산기의 논리식을 이용하여 2비트 전가산기의 논리식을 도출합니다.
-. 1비트 전가산기의 논리식
- S = (A XOR B) XOR Cin
- Cout = (A AND B) OR (Cin AND (A XOR B))
-. 2비트 전가산기의 논리식
- 첫 번째 비트(LSB)
S0 = (A0 XOR B0) XOR Cin
C1 = (A0 AND B0) OR (Cin AND (A0 XOR B0)) - 두 번째 비트(MSB)
S1 = (A1 XOR B1) XOR C1
Cout = (A1 AND B1) OR (C1 AND (A1 XOR B1))
3단계 : 회로 설계
2비트 전가산기는 두 개의 1비트 전가산기를 직렬로 연결하여 설계합니다.
각 전가산기의 출력 캐리(Carry)는 다음 비트의 입력 캐리(Cin)로 사용됩니다.
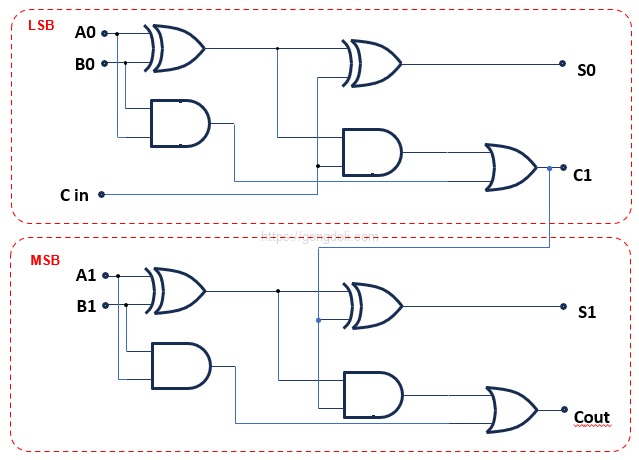
3-2) 4비트 가산기 설계 예제
이진 가산기 회로 설계에서 4비트 가산기는 두 개의 4비트 이진수를 더하는 회로입니다.
이는 4개의 1비트 전가산기를 직렬로 연결하여 설계할 수 있습니다.
각 비트의 합과 자리올림을 계산하는 단계로 구성됩니다.
1단계 : 1비트 전가산기의 진리표와 논리식
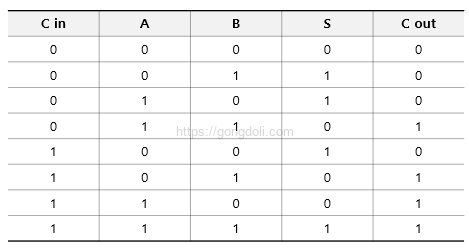
각 1비트 전가산기는 다음과 같은 논리식을 가집니다.
- S = (A XOR B) XOR Cin
- Cout = (A AND B) OR (Cin AND (A XOR B))
2단계 : 4비트 가산기의 설계
4개의 1비트 전가산기를 직렬로 연결하여 4비트 가산기를 설계합니다.
각 전가산기의 출력 캐리(Cout)는 다음 비트의 입력 캐리(Cin)로 사용됩니다.
-. 1비트 전가산기 구성
- 첫 번째 1비트 전가산기 (LSB)
입력: A0, B0, Cin
출력: S0, C1 - 두 번째 1비트 전가산기
입력: A1, B1, C1
출력: S1, C2 - 세 번째 1비트 전가산기
입력: A2, B2, C2
출력: S2, C3 - 네 번째 1비트 전가산기 (MSB)
입력: A3, B3, C3
출력: S3, Cout
3단계 : 회로 구현 단계별 설명
- 첫 번째 1비트 전가산기 (LSB)
XOR 게이트를 사용하여 A0와 B0의 XOR 값을 구합니다.
두 번째 XOR 게이트를 사용하여 첫 번째 XOR 값과 Cin의 XOR 값을 구하여 S0를 얻습니다.
AND 게이트와 OR 게이트를 사용하여 자리올림(C1)을 구합니다. - 두 번째 1비트 전가산기
XOR 게이트를 사용하여 A1과 B1의 XOR 값을 구합니다.
두 번째 XOR 게이트를 사용하여 첫 번째 XOR 값과 C1의 XOR 값을 구하여 S1을 얻습니다.
AND 게이트와 OR 게이트를 사용하여 자리올림(C2)을 구합니다. - 세 번째 1비트 전가산기
XOR 게이트를 사용하여 A2와 B2의 XOR 값을 구합니다.
두 번째 XOR 게이트를 사용하여 첫 번째 XOR 값과 C2의 XOR 값을 구하여 S2를 얻습니다.
AND 게이트와 OR 게이트를 사용하여 자리올림(C3)을 구합니다. - 네 번째 1비트 전가산기 (MSB)
XOR 게이트를 사용하여 A3과 B3의 XOR 값을 구합니다.
두 번째 XOR 게이트를 사용하여 첫 번째 XOR 값과 C3의 XOR 값을 구하여 S3을 얻습니다.
AND 게이트와 OR 게이트를 사용하여 최종 자리올림(Cout)을 구합니다.
4단계 : 회로 다이어그램
4비트 가산기의 회로 다이어그램은 다음과 같습니다.
각 전가산기는 위의 논리식에 따라 구성됩니다.
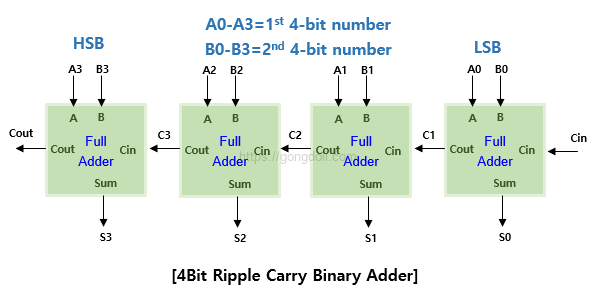
여기서 각각 1비트 전가산기를 나타내며, 각 전가산기의 출력 캐리(Cout)는 다음 전가산기의 입력 캐리(Cin)로 사용됩니다.
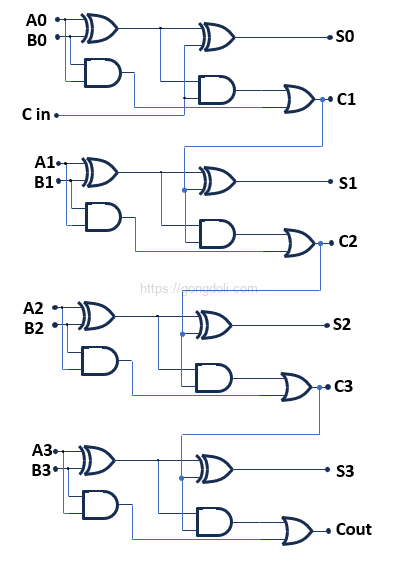
예를 들어, A = 1011 (10진수로 11), B = 1101 (10진수로 13)인 경우를 계산해 보겠습니다.
- LSB(첫 번째 비트) 전가산기
A0 = 1, B0 = 1, Cin = 0
S0 = 0, C1 = 1 - 두 번째 비트 전가산기
A1 = 1, B1 = 0, Cin = 1
S1 = 0, C2 = 1 - 세 번째 비트 전가산기
A2 = 0, B2 = 1, Cin = 1
S2 = 0, C3 = 1 - MSB(네 번째 비트) 전가산기
A3 = 1, B3 = 1, Cin = 1
S3 = 1, Cout = 1
즉 최종 결과는 Sum = 11000 (10진수로 24), 최종 캐리(Cout) = 1