Contents
1. RC 적분기란 무엇인가?
1-1) 적분기의 기본 개념
RC 적분기는 입력 신호의 “적분”을 수행하는 회로입니다.
즉, 입력 신호가 시간에 따라 어떻게 변화하는지 기록하여 이를 누적한 값을 출력으로 내보냅니다.
이 과정에서, 입력 신호가 크면 출력이 빠르게 증가하고, 입력 신호가 작으면 출력이 느리게 변하게 됩니다.
RC 적분기의 주요 요소는 저항(R)과 커패시터(C)이며, 이들이 어떻게 연결되는지에 따라 회로의 동작이 달라집니다.
적분기의 기본적인 역할은 입력 신호의 누적 값을 계산하는 것으로, 주로 저주파 신호를 처리하는 데 사용됩니다.
1-2) RC 적분기와 RC 미분기의 차이점
RC 적분기와 RC 미분기는 신호 처리에서 상반된 역할을 합니다.
RC 미분기는 입력 신호의 변화율(즉, 기울기)을 출력으로 내보냅니다.
반면, RC 적분기는 입력 신호의 변화들을 누적하여 전체적인 신호의 크기를 출력합니다.
- RC 미분기: 입력 신호의 순간적인 변화에 민감하며, 급격한 변화가 있을 때 출력에서 스파이크처럼 날카로운 신호를 나타냅니다.
신호의 가장 큰 변화 부분을 강조하는 역할을 합니다. - RC 적분기: 신호의 변화가 시간이 지남에 따라 축적됩니다.
따라서 완만한 변화나 일정한 신호에서도 출력이 지속적으로 증가하거나 감소합니다.
신호의 누적된 에너지를 출력하는 특성이 있습니다.
이렇게, RC 적분기 동작 원리는 신호를 천천히 축적하여 입력의 전반적인 경향을 나타내는 데 중점을 둔 회로입니다.
이를 통해 신호의 큰 흐름을 파악할 수 있어, 필터나 데이터 신호 처리에 유용하게 쓰입니다.
- 연관 참조 : RC 충전, RC 회로 충전 시간, 충전 과정, 시간 상수, 전압.전류 변화
- 연관 참조 : RC 회로 방전 시간,전압 변화, 시간 상수, 예시1
- 연관 참조 : 미분기,회로 수식,RC 미분기 동작 원리,입력 파형에 따른 출력 파형, 예제1
- 연관 참조 : RC 회로 상수 계산기, 장점 및 단점, 사용 방법
2. RC 적분기의 회로 구성과 동작 원리
2-1) 회로 구성 요소 설명
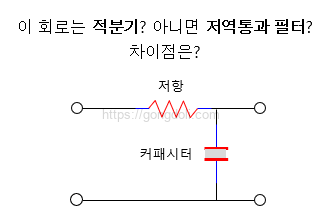
RC 적분기는 간단하게 저항(R)과 커패시터(C)로 이루어진 회로입니다.
이 두 가지 구성 요소의 연결 방식에 따라 입력 신호의 적분이 이루어지며, 회로의 특성이 결정됩니다.
RC 적분기의 기본적인 회로 구성은 다음과 같습니다.
- 저항(R): 입력 신호가 먼저 저항을 통과하게 되는데, 저항은 신호가 커패시터로 들어가는 속도를 조절합니다.
저항 값이 클수록 신호가 천천히 변하게 되며, 반대로 저항 값이 작을수록 신호가 빠르게 변화합니다. - 커패시터(C): 저항을 통과한 신호가 커패시터에 축적됩니다.
커패시터는 전압을 축적하는 특성을 가지고 있어, 입력 신호가 시간이 지남에 따라 커패시터에 축적되면서 출력 신호가 점차 증가하거나 감소하게 됩니다.
RC 적분기는 고정된 저항이 커패시터와 직렬로 연결된 것으로, 커패시터는 주파수에 따라 달라지는 리액턴스(Xc)를 가지고 있습니다.
주파수가 낮을 때는 커패시터의 리액턴스가 높아지며, 주파수가 높을 때는 리액턴스가 낮아집니다.
이는 표준적인 커패시터 리액턴스 공식인 Xc = 1/(2πƒC)으로 설명할 수 있습니다.
이 현상은 패시브 저역 통과 필터(Low Pass Filter, LPF)에서 나타나며, RC 회로에서 쉽게 볼 수 있는 특성입니다.
만약 입력 신호가 사인파라면, RC 적분기는 일정 주파수 이상에서 단순한 저역 통과 필터처럼 동작하게 됩니다.
이 필터는 컷오프 주파수 이상의 신호를 감소시키며, 컷오프 주파수는 회로의 RC 시간 상수(tau, τ)와 일치합니다.
순수한 사인파가 입력되었을 때 RC 적분기는 패시브 저역 통과 필터처럼 작동하여, 컷오프 주파수 이상의 신호는 출력에서 감소하게 됩니다.
미분기 설명할때도 애기했듯이, RC 시간 상수는 저항과 커패시턴스의 시간에 대한 관계를 나타냅니다.
이 시간 상수는 초 단위로 측정되며, 저항(R)과 커패시터(C)의 곱에 비례합니다.
즉, 회로에서 커패시터의 충전 또는 방전 속도는 이 RC 시간 상수에 의해 결정됩니다.
결론적으로, RC 적분기 회로는 입력 신호의 변화에 따라 커패시터가 충전되고 방전되면서, 출력에서 신호의 적분된 값이 나타나도록 동작합니다.
이러한 RC 적분기 동작 원리는 특히 필터링 응용 분야에서 유용하게 사용되며, 주파수에 따른 신호 처리에 중요한 역할을 합니다.
2-2) RC 적분기의 동작 원리
RC 적분기의 동작 원리는 신호를 시간에 따라 적분하여 출력하는 과정입니다.
다시 말해, 입력 신호가 커패시터에 충전되면서 시간에 따른 전압 변화가 누적되고, 그 결과 출력에서 신호의 “적분” 값이 나타나게 됩니다.
이를 조금 더 구체적으로 설명하면, 입력 신호가 RC 적분기에 인가될 때 저항을 거친 신호가 커패시터로 흐르게 됩니다.
이때 커패시터는 즉각적으로 신호를 반영하지 않고, 입력 신호가 계속 유지되면 커패시터에 전하가 점차 쌓이게 됩니다.
이 과정이 바로 신호의 적분입니다.
입력 신호가 변하지 않고 일정하게 유지되면, 커패시터는 계속 충전되어 출력 전압이 서서히 증가합니다.
반대로 입력 신호가 감소하면, 커패시터는 방전되어 출력 전압이 감소하게 됩니다.
이렇듯 입력 신호의 변화가 지속적으로 커패시터에 반영되면서, 신호의 전체적인 흐름이 출력에서 나타나게 됩니다.
“어떻게 단순한 회로가 신호를 적분할 수 있는가?”라는 질문을 한다면, 그 답은 바로 커패시터의 특성에 있습니다.
커패시터는 전압을 천천히 축적하거나 방전하는 특성을 가지고 있기 때문에, 시간이 지남에 따라 신호가 어떻게 변화했는지를 반영하는 적분 회로로 동작할 수 있습니다.
이처럼 RC 적분기 동작 원리는 신호가 시간에 따라 어떻게 변해왔는지를 누적하여 출력하는 과정으로 설명됩니다.
입력 신호가 시간이 지남에 따라 어떻게 축적되는지에 따라 출력 신호가 결정되므로, 이러한 특성을 잘 이해하면 RC 적분기의 동작을 명확히 파악할 수 있습니다.
RC 적분기 동작 원리를 더 깊이 이해하기 위해, 단일 펄스 신호를 회로에 적용해 보겠습니다.
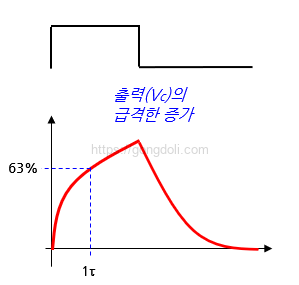
입력에 단일 펄스가 들어오면, 커패시터는 저항을 통해 충전됩니다.
그러나 커패시터는 즉시 충전되지 않고, 충전 속도는 RC 시간 상수에 따라 지수적으로 증가합니다.
입력 펄스가 끝나면, 커패시터는 다시 방전되기 시작하며, 출력 신호는 역시 지수적으로 감소하게 됩니다.
충전은 커패시터가 충전될 때, 전압은 다음과 같은 식으로 증가합니다.
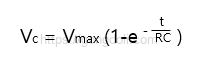
방전은 커패시터가 방전될 때 전압은 다음과 같이 감소합니다.
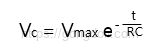
이 두 식은 RC 적분기 동작 원리에 따라 커패시터가 어떻게 시간에 따라 전압을 적분하고 저장하는지를 보여줍니다.
2-3) 커패시터의 전류와 충전 속도
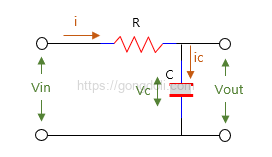
커패시터에 흐르는 전류는 다음과 같이 표현됩니다.
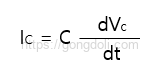
이 식은 커패시터 전압의 시간에 따른 변화율에 따라 커패시터에 흐르는 전류가 결정된다는 것을 나타냅니다.
또 다른 표현으로, 전류는 전하의 시간에 따른 변화율로 나타낼 수 있으며, 이를 다음과 같이 쓸 수 있습니다.
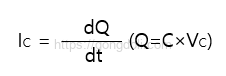
여기서 전하 Q는 커패시터에 쌓이는 전압에 비례합니다.
RC 적분기 동작 원리에서 중요한 점은 커패시터가 충전되거나 방전되는 속도가 저항 R과 커패시터 C의 값에 의해 결정된다는 것입니다.
이 두 값의 곱은 RC 시간 상수로 나타내며, 이는 회로에서의 충전/방전 속도를 결정합니다.
RC 적분기 회로의 시간 상수는 저항 R과 커패시터 C의 곱으로 정의됩니다.
τ=R×C
이 시간 상수는 커패시터가 최대 전압의 63.2%까지 충전되거나, 방전 시 36.8%로 떨어지는 데 걸리는 시간을 나타냅니다.
이 값은 RC 적분기 동작 원리에서 매우 중요한 요소입니다.
커패시터가 충전되거나 방전되는 시간은 R과 C에 따라 달라지며, 이 값이 커질수록 충전과 방전이 느려집니다.
RC 적분기 동작 원리에 따르면, 입력 신호는 저항을 통해 커패시터로 전달되며, 커패시터에서 출력 전압이 나타납니다.
입력 신호가 일정한 전압일 때, 커패시터는 시간이 지남에 따라 충전되고 출력 전압은 지수 함수적으로 증가합니다.
이때 출력 전압은 입력 전압의 적분 값에 해당하며, 이 적분 과정이 회로에서의 핵심 역할을 합니다.
입력 신호가 주어졌을 때, 출력 전압은 시간에 따른 입력 전압의 적분으로 표현할 수 있습니다.
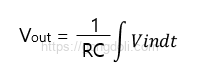
이 식은 RC 적분기 동작 원리의 본질을 설명하며, 입력 신호가 시간이 지남에 따라 적분되어 출력으로 나타남을 보여줍니다.
3. 적분기 회로 예제
RC 적분기 동작 원리에 대해 자세히 설명하기 위해, 구체적인 회로 예시를 들어보겠습니다.
입력 신호가 회로에 어떻게 영향을 미치는지 설명하겠습니다.
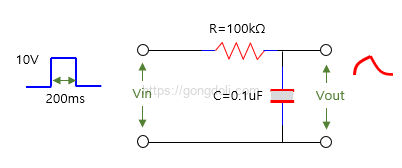
우선, RC 적분기 회로의 시간 상수를 계산해야 합니다.
시간 상수,𝜏는 저항R과 커패시터C의 곱으로 정의되며, 이를 통해 회로의 충전 및 방전 속도를 결정할 수 있습니다.
예를 들어, 위에 그림처럼 저항R이 100kΩ이고 커패시터C가 1μF인 경우 시간 상수는 다음과 같이 계산됩니다.
τ=R×C=100kΩ×1μF=100ms
이 값은 커패시터가 회로에서 충전되거나 방전되는 데 걸리는 시간의 중요한 지표입니다.
RC 적분기 동작 원리에 따르면, 이 시간 상수는 출력 전압이 입력 신호를 따라 어떻게 변화하는지를 결정하는 요소입니다.
이제 입력 신호로 스텝 전압 펄스를 회로에 가해보겠습니다.
가령, 펄스의 지속 시간이 시간 상수의 두 배인 200ms라고 가정해 보겠습니다.
이 경우 RC 적분기 동작 원리에 따르면, 커패시터는 입력 신호에 따라 충전되고, 시간이 지남에 따라 전압이 증가합니다.
RC 적분기 동작 원리에 따르면, 커패시터는 지수적으로 충전되며, 시간 상수 2τ(200ms) 동안 커패시터는 최대 충전량의 약 86.4%까지 충전됩니다.
입력 펄스의 크기가 10V라고 가정하면, 커패시터의 전압은 다음과 같이 증가합니다.
VC=10V×0.864=8.64V
즉, 커패시터는 8.64V까지 충전된 후, 입력 신호가 0으로 돌아가면 저항을 통해 다시 방전되기 시작합니다.
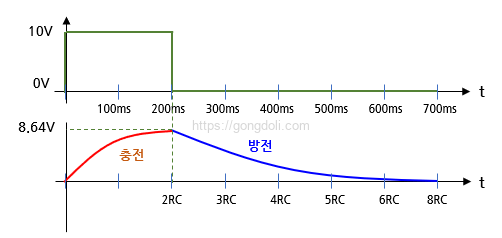
RC 적분기 동작 원리에 따르면, 커패시터는 입력 신호가 0이 되면 방전됩니다.
이때 방전 속도 역시 시간 상수 τ=100ms에 따라 결정됩니다.
커패시터가 완전히 방전되기까지는 일반적으로 5τ, 즉 500ms가 걸리며, 그동안 커패시터의 전압은 지수적으로 감소하게 됩니다.
입력 펄스가 주기적으로 발생하며, 그 사이에 커패시터가 충분히 방전될 시간을 가지면, 회로는 안정적인 적분 동작을 유지할 수 있습니다.
다시 말해, 커패시터는 매 펄스마다 입력 신호를 적분하고, 출력 신호는 그 결과로 나타납니다.
입력 펄스가 10V의 크기와 200ms의 지속 시간을 가지고 있을 때, 커패시터의 충전 및 방전 과정은 다음과 같은 곡선으로 나타낼 수 있습니다.
입력 신호가 들어오면 커패시터는 8.64V까지 충전되며, 이후 입력이 0V로 돌아가면 커패시터는 저항을 통해 방전됩니다.
이러한 과정은 반복되며, 출력 전압은 입력 신호의 적분에 따라 변합니다.
이처럼, RC 적분기 동작 원리에 따라 입력 신호의 크기와 시간 상수에 따라 커패시터의 충전 및 방전 과정이 결정되고, 출력 신호는 이에 따라 변화합니다.
입력 신호가 커질수록 커패시터는 더 높은 전압까지 충전되고, 반대로 입력 신호가 작거나 시간이 짧을수록 커패시터는 더 낮은 전압에서 방전됩니다.
4. 입력 신호에 따른 출력 변화
RC 적분기 회로에서 입력 신호가 어떤 형태인지에 따라 출력 신호의 특성이 크게 달라집니다.
RC 적분기 동작 원리는 입력 신호의 형태를 적분하여 출력 신호로 만들어내기 때문에, 입력 신호가 정현파인지, 삼각파인지, 혹은 다른 형태인지를 이해하는 것이 중요합니다.
4-1) 정현파와 삼각파 입력에 대한 출력 특성
정현파(Sine Wave) 입력에 대한 출력 정현파를 RC 적분기의 입력으로 넣으면 출력 신호는 무엇을 적분하느냐에 따라 달라집니다.
정현파는 수학적으로 일정한 주기를 가지며 부드럽게 오르내리는 파형이기 때문에, 이를 적분한 출력 신호는 원래의 정현파에 90도 위상이 이동된 형태가 됩니다.
예를 들어, 만약 입력으로 순수한 사인파가 주어졌다면, RC 적분기는 이 사인파의 적분 결과로 코사인파를 출력하게 됩니다.
이는 회로가 주파수에 따라 신호를 저역 통과 필터처럼 처리하기 때문에 주파수가 낮은 신호를 그대로 전달하며, 이를 적분하여 위상이 이동된 신호를 출력하는 방식입니다.
즉, RC 적분기 동작 원리에 따라 정현파 입력은 일정한 주기를 가지는 부드러운 코사인파 출력으로 변환됩니다.
이 과정에서 출력의 진폭은 입력 주파수와 RC 시간 상수에 의해 조절됩니다.
삼각파(Triangle Wave) 입력에 대한 출력 삼각파 입력은 직선적으로 상승하고 하강하는 특성을 가지고 있습니다.
삼각파의 적분을 수행하면, 출력 신호는 곡선적으로 변형된 파형이 됩니다.
삼각파는 선형적인 변화이기 때문에, 이를 적분하면 출력은 기울어진 구간에서 곡선을 형성하며 포물선(parabolic) 모양의 신호가 나타납니다.
삼각파는 일정하게 상승하는 부분과 일정하게 하강하는 부분으로 나뉘는데, RC 적분기는 이 변화를 인식하여 이를 적분한 곡선 형태로 출력합니다.
따라서 출력 신호는 매우 부드럽고 둥근 파형이 되며, 삼각파보다 더욱 느린 변화의 특징을 가집니다.
4-2) 다양한 입력 신호에 따른 출력 분석
펄스 신호 (Pulse Wave) 펄스 신호는 매우 짧은 시간 동안의 빠른 변화가 특징입니다.
펄스 입력 신호를 RC 적분기에 적용하면, 출력 신호는 펄스의 빠른 상승과 하강 구간을 적분한 결과로 나타납니다.
펄스의 빠른 상승 부분을 적분하면 출력은 천천히 상승하며, 반대로 펄스가 빠르게 내려가는 부분에서는 출력이 천천히 감소합니다.
결과적으로 펄스 신호의 출력은 계단형 파형처럼 보이게 됩니다.
구형파 (Square Wave) 구형파는 일정한 주기를 가지고 갑작스럽게 상승하고 하강하는 특성이 있습니다. 구형파를 적분하면 출력은 천천히 증가하거나 감소하는 형태가 됩니다.
이는 구형파의 빠른 상승 구간이 적분되어 출력에서 선형적으로 증가하는 구간으로 나타나고, 빠른 하강 구간이 적분되어 선형적으로 감소하는 구간으로 변환되기 때문입니다.
이로 인해 구형파 입력에 대한 출력은 삼각파와 유사한 형태가 됩니다.
복잡한 신호 (Complex Waveform) 복잡한 신호는 다양한 주파수와 파형을 혼합한 입력 신호를 의미합니다.
이러한 신호를 RC 적분기에 입력하면, 출력은 각 주파수 성분을 적분한 결과로 다양한 파형들이 겹쳐 나타나게 됩니다.
특히 주파수가 높은 성분일수록 적분에 의해 출력에서 부드럽게 처리되며, 주파수가 낮은 성분은 적분 결과 큰 영향을 미치지 않게 됩니다.
결론적으로, RC 적분기 동작 원리는 입력 신호의 형태에 따라 출력에서 매우 다른 파형을 생성할 수 있습니다.
정현파는 위상이 이동된 코사인파로, 삼각파는 곡선형 파형으로, 구형파는 삼각파로 변환되며, 다양한 입력 신호는 이 적분 과정을 통해 각기 다른 출력 신호를 만들어냅니다.

I have been reading out some of your stories and i can claim pretty nice stuff. I will definitely bookmark your blog.
Thank you so much for your kind words! I’m thrilled you enjoy the stories and appreciate you bookmarking the blog
I simply couldn’t leave your site before suggesting that I actually enjoyed the usual information a person supply for your visitors? Is gonna be again regularly in order to investigate cross-check new posts.
That truly means a lot—thank you! I’m so glad the regular content resonated with you.
It’s perfect time to make a few plans for the long run and it’s time to be happy. I have learn this post and if I may just I want to suggest you few attention-grabbing things or suggestions. Maybe you could write subsequent articles referring to this article. I wish to read even more issues approximately it!
Thank you so much for your thoughtful message!
I’m really glad the post resonated with you.
I’d love to hear your suggestions, and I’ll definitely keep them in mind for future articles.
It means a lot that you’re interested in reading more!
Good post. I study one thing more challenging on different blogs everyday. It’s going to all the time be stimulating to learn content material from different writers and follow a little bit one thing from their store. I’d favor to make use of some with the content material on my weblog whether or not you don’t mind. Natually I’ll offer you a link in your net blog. Thanks for sharing.
Thank you so much for your kind words and thoughtful approach!
I’m glad you found the content engaging and inspiring.
Feel free to use parts of it on your blog—as long as you include a link back, that’s absolutely fine.
Saved as a favorite, I really like your blog!
Thanks a lot—so glad you liked it!
he blog was how do i say it… relevant, finally something that helped me. Thanks
Happy it was helpful—thanks for sharing your thoughts!
Absolutely pent content, Really enjoyed studying.
Thank you for your kind words. I’m glad you enjoyed reading the content.
As I web site possessor I believe the content material here is rattling excellent , appreciate it for your efforts. You should keep it up forever! Best of luck.
Thank you for your kind words. I truly appreciate your encouragement and support.