Contents
1. 조합 논리 회로란?
1-1) 정의 및 개요
조합 논리 회로(Combinational Logic Circuit)는 디지털 회로의 기본적인 구성 요소 중 하나로, 입력 신호에 의해 즉시 출력이 결정되는 회로입니다.
이 회로는 이전 상태나 시간적 변화와 무관하게 현재 입력에 따라서만 동작합니다.
즉, 입력과 출력 간의 직접적인 관계가 있으며, 이는 조합 논리 회로가 매우 빠르게 동작할 수 있게 합니다.
조합 논리 회로는 여러 개의 논리 게이트로 구성됩니다.
논리 게이트는 기본적인 논리 연산을 수행하는 소자로, 대표적인 예로는 AND, OR, NOT 게이트가 있습니다.
이러한 게이트를 조합하여 복잡한 논리 연산을 수행할 수 있으며, 다양한 디지털 장치에서 사용됩니다.
간단한 예로 디지털 도어락을 생각해 볼 수 있습니다.
디지털 도어락은 특정한 비밀번호 입력(입력 신호)에 따라 문을 열거나 닫는 동작(출력 신호)을 합니다.
이때, 입력된 비밀번호가 올바르면 문이 열리고, 틀리면 문이 닫힌 채로 유지됩니다.
이러한 동작은 현재 입력된 비밀번호에만 의존하며, 이전에 입력된 비밀번호와는 상관없습니다.
이처럼, 조합 논리 회로는 입력된 신호만을 고려하여 즉시 출력을 결정합니다.
조합 논리 회로는 진리표(Truth Table)와 부울 대수(Boolean Algebra)를 사용하여 설계됩니다.
진리표는 모든 가능한 입력 조합에 대해 대응되는 출력을 명시한 표로, 이를 기반으로 회로의 동작을 정의할 수 있습니다.
부울 대수는 논리 연산을 수학적으로 표현하는 방식으로, 회로 설계에서 중요한 역할을 합니다.
1-2) 순차 논리 회로와의 차이점
조합 논리 회로와 순차 논리 회로는 디지털 회로 설계에서 중요한 두 가지 개념입니다.
이 둘은 여러 면에서 차이가 있으며, 이를 이해하는 것이 회로 설계의 기초를 이해하는 데 중요합니다.
- 조합 논리 회로는 현재 입력에 따라 즉시 출력이 결정됩니다.
이전 입력이나 상태는 출력에 영향을 주지 않습니다. - 순차 논리 회로는 현재 입력뿐만 아니라 이전 상태에도 의존하여 출력이 결정됩니다.
시간의 흐름과 내부 상태 정보가 중요한 역할을 합니다.
조합 논리 회로는 입력에 의존하여 즉각적인 출력을 생성하는 디지털 회로로, 논리 게이트를 통해 구현됩니다.
이는 과거 상태나 시간적 변화를 고려하지 않고, 현재 입력만을 기반으로 동작합니다.
이와는 달리, 순차 논리 회로는 입력뿐만 아니라 이전 상태와 클럭 신호에 따라 동작이 변화합니다.
조합 논리 회로는 단순함과 빠른 응답 시간이 필요로 하는 여러 응용 분야에서 널리 사용됩니다.
예를 들어, 기본적인 논리 연산, 데이터 라우팅, 디지털 신호 처리 등에서 조합 논리 회로는 핵심적인 역할을 합니다.
이를 통해 우리는 컴퓨터나 디지털 시스템에서 복잡한 연산과 처리를 신속하게 수행할 수 있습니다.
- 연관 참조 : 이진 감산기 회로 설계, 직렬과 병렬 감산기 비교, 회로 설계 예제 3가지
- 연관 참조 : 비교기 회로 설계, 유형, 회로 설계 방법, 예제, 주의 사항 7가지
- 연관 참조 : 이진 가산기 회로 설계, 회로 설계 방법, 예제 설계 2가지
- 연관 참조 : 2진 디코더 회로 설계, 회로 설계 방법, 예제,설계 문제 4가지
- 연관 참조 : Encoder 회로 설계, 회로 설계 방법, 예제, 흔한 설계 문제 4가지
- 연관 참조 : Demultiplexer 회로 설계, 회로 설계 방법, 예제, 흔한 설계 문제 5가지
- 연관 참조 : Multiplexer 회로 설계,유형과 종류,회로 설계 방법, 예제
2. 조합 논리 회로의 설계
조합 논리 회로의 설계는 디지털 회로의 핵심적인 부분으로, 입력 신호에 따라 특정한 논리적 출력을 생성하는 과정을 포함합니다.
조합 논리 회로는 이전 상태에 의존하지 않고, 현재 입력 신호만을 고려하여 출력을 즉각적으로 생성하는 특성을 가지고 있습니다.
이를 설계하는 방법에는 여러 가지가 있으며, 여기서는 부울 대수식, 진리표와 카르노 맵, 그리고 최소화 기법 및 회로 최적화에 대해 설명하겠습니다.
2-1) 부울 대수식을 이용한 회로 설계
부울 대수식(Boolean Algebra)은 조합 논리 회로 설계의 기초입니다.
부울 대수는 논리 연산을 수학적으로 표현하며, 이를 통해 회로의 동작을 정의하고 최적화할 수 있습니다.
- 부울 대수식의 기초
부울 대수는 AND, OR, NOT 연산을 사용하여 논리 표현식을 만듭니다.
예를 들어, 두 개의 입력 A와 B에 대한 AND 연산은 A×B 또는 AB로 표현되며, 이는 A와 B가 모두 참일 때만 참을 출력합니다.
OR 연산은 A+B로 표현되며, A나 B 중 하나라도 참일 때 참을 출력합니다.
NOT 연산은 ‾A 또는 A′ 로 표현되며, A가 참일 때 거짓을, 거짓일 때 참을 출력합니다.
- 부울 대수식을 이용한 회로 설계
먼저, 요구 사항을 분석하여 회로가 어떤 논리적 기능을 수행해야 하는지 결정합니다.
이를 바탕으로 입력 변수와 출력 변수 간의 관계를 정의하는 불 대수식을 작성합니다.
예를 들어, 두 개의 입력 A와 B를 받아 출력 C를 생성하는 회로가 AND 연산을 수행해야 한다면, C는 A×B로 정의됩니다.
부울 대수식을 기반으로 논리 게이트를 조합하여 회로를 구성합니다.
간단한 예로, 세 개의 입력 A, B, C가 주어졌을 때, 출력 Z가 다음과 같이 정의된다고 가정해 보겠습니다.
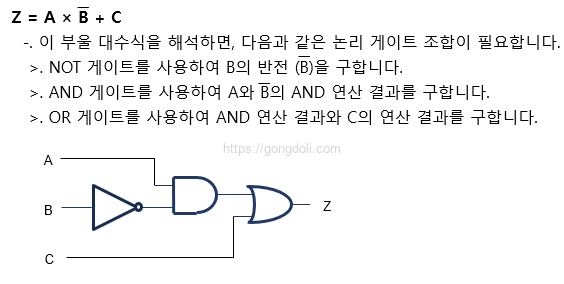
이러한 과정을 통해 조합 논리 회로의 구조를 도출할 수 있습니다.
2-2) 진리표와 카르노 맵(Karnaugh Map)
조합 논리 회로의 설계에서 진리표(Truth Table)와 카르노 맵(Karnaugh Map)은 중요한 도구입니다.
이들은 회로의 논리적 동작을 시각적으로 표현하고, 이를 최적화하는 데 유용합니다.
진리표(Truth Table)
진리표는 모든 가능한 입력 조합에 대해 해당하는 출력을 명시하는 표입니다.
이를 통해 회로의 동작을 명확하게 이해할 수 있습니다.
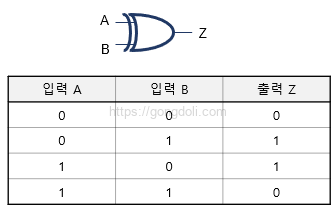
예를 들어, 두 개의 입력 A와 B가 주어졌을 때, 이들의 모든 조합과 해당 출력 Z를 진리표로 작성하면 다음과 같습니다.
이 진리표는 XOR 게이트의 동작을 설명하는 것으로, 입력 A와 B가 다를 때 출력 Z가 1임을 나타냅니다.
카르노 맵(Karnaugh Map)
카르노 맵은 진리표의 정보를 시각적으로 정리하여 논리식을 간단하게 최소화할 수 있는 도구입니다.
이는 2차원 또는 3차원 표 형태로 구성되어, 인접한 셀들이 논리적으로 연관된 값을 가지도록 배치됩니다.
예를 들어, F=A’B’C+A’BC+A’BC’+ABC’를 카르노 맵을 이용해서 간소화 해보겠습니다.
우선, 주어진 논리식을 바탕으로 진리표를 작성해 봅시다. 각 항은 다음과 같은 입력 조합에 대해 출력을 1로 만듭니다.
- A′B′C는 A=0,B=0,C=1일 때 1.
- A′BC는 A=0,B=1,C=1일 때 1.
- A′BC′는 A=0,B=1,C=0일 때 1.
- ABC′는 A=1,B=1,C=0일 때 1.
이것을 진리표로 나타내면
이제 카르노 맵에 위의 진리표를 매핑해 보겠습니다.
3개의 변수를 사용하는 3×2 카르노 맵은 다음과 같이 그립니다:
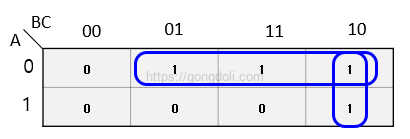
카르노 맵에서 인접한 ‘1’들을 그룹화합니다.
그룹화할 수 있는 최대 크기의 직사각형 또는 정사각형 그룹을 찾아야 합니다.
따라서 최소화된 식은 F=A’+BC’ 입니다.
회로 최적화
최소화된 논리식을 바탕으로 회로의 설계를 간소화하여 불필요한 논리 게이트를 제거합니다.
예를 들어, 복잡한 다단계 논리 회로를 단일 단계로 줄이거나, 공통된 논리 연산을 공유하는 게이트를 합치는 방법으로 최적화할 수 있습니다.
이를 통해 회로의 크기, 전력 소모, 응답 시간을 줄일 수 있습니다.