Contents
1. 개요
저항은 직렬 연결, 병렬 연결 또는 직렬 및 병렬 저항의 조합을 통해 더 복잡한 저항 연결을 구성할 수 있습니다.
직렬 저항의 경우 등가 저항은 직렬로 연결된 개별 저항의 수학적 조합으로 계산됩니다.
저항은 전압을 전류로 변환하거나 전류를 전압으로 변환하는 데 사용되는 기본 전자 부품일 뿐만 아니라,
값의 조절을 통해 변환된 전류나 전압에 다른 가중치를 부여하여 전압 기준 회로 및 응용 프로그램에 활용될 수 있습니다.
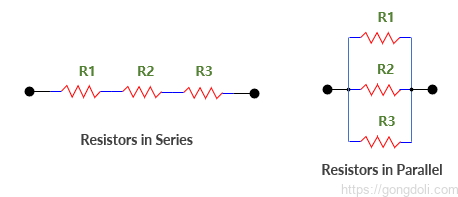
직렬 또는 직렬 및 병렬 저항 계산과(아래 참조) 같은 복합적인 저항 연결의 경우 단일한 등가 저항으로 대체될 수 있습니다.
등가 저항 또는 임피던스와 같은 용어로 사용되며, 저항 연결의 복잡성과 관계없이 모든 저항은 오옴의 법칙과 키르히호프의 회로 법칙을 기본적으로 따릅니다.
직렬 및 병렬 저항 계산과 같은 용어는 다양한 저항 구성의 전기적 특성을 계산하고 이해하는 데 중요한 역할을 합니다.
- 연관 참조 : 오옴의 법칙 원리, 개념, 예제로 이해하기,전력 구하기,파이 차트
- 연관 참조 : 저항기 종류와 장단점, 저항률이란?,저항 vs. 저항률, 종류12가지
- 연관 참조 : 저항값 색상 코드,색상 코드 표, 저항값 읽는 방법,SMD 읽는 방법
- 연관 참조 : 저항과 저항률(resistivity), 개념, 차이, 예제 풀이,중요성
2. 직렬 저항의 이해
직렬 및 병렬 저항 계산에서 직렬 저항은 저항이 한 줄로 늘어선 형태로 연결되었다고 생각하면 됩니다.
첫 번째 저항을 통과하는 전류는 다른 저항을 통해 흐를 수밖에 없기 때문에 두 번째 저항과 세 번째 저항을 지나야 합니다.
따라서 직렬로 연결된 저항들은 하나의 경로를 통해 흐를 수 있기 때문에 전류는 모든 저항을 통과하며 동일합니다.
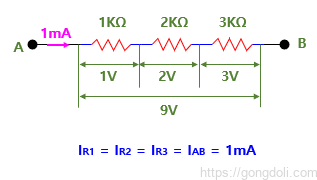
2-1) 직렬 저항 회로
직렬 및 병렬 저항 계산에서 직렬 저항 회로는 저항들이 직렬로 연결되어 있기 때문에 전류는 연결된 모든 저항을 통과하며,
회로의 총 저항인 RT는 모든 개별 저항의 합과 같아야 합니다.
즉, RT=R1+R2+R3
위의 간단한 예시에서 저항의 개별 값들을 가지고, 총 등가 저항인REQ는 다음과 같이 주어집니다
REQ=R1+R2+R3=1kΩ+2kΩ+6kΩ=9kΩ
위의 예시에서 볼 수 있듯이, 세 개의 개별 저항을 하나의 9kΩ 등가 저항으로 대체할 수 있습니다.
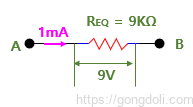
네 개, 다섯 개 또는 그 이상의 저항이 모두 직렬로 연결된 회로에서는 회로의 총 또는 등가 저항인RT는 여전히 모든 개별 저항을 합한 값이 됩니다.
그리고, 저항이 추가될수록 등가 저항도 커지게 됩니다.
이 총 저항은 일반적으로 등가 저항으로 알려져 있으며, “회로 내의 전류나 전압 값에 영향을 주지 않고 직렬로 연결된 모든 저항을 대체할 수 있는 단일 저항 값”으로 정의될 수 있습니다.
따라서 저항을 직렬로 연결하여 회로의 총 저항을 계산하는 공식은
Rtotal = R1 + R2 + R3 + ….. Rn
2-2) 직렬 저항 등가 회로
직렬 및 병렬 저항 계산에서 직렬 저항의 등가 저항 또는 총 저항인 RT은 개별 저항의 대수적 합과 동일한 회로에 대해 동일한 효과를 갖습니다.
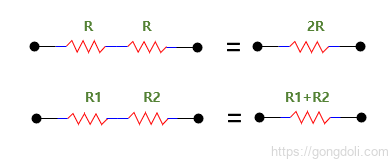
- 직렬로 연결된 동일한 저항: 만약 두 개의 저항 또는 임피던스가 동일하고 같은 값인 경우, 총 또는 등가 저항 RT는 한 저항의 값의 두 배가 됩니다.
즉, 2R이며, 세 개의 동일한 저항이 직렬로 연결된 경우, 3R 등이 됩니다. - 직렬로 연결된 불균형한 저항: 만약 두 개의 저항 또는 임피던스가 불균형하고 서로 다른 값인 경우, 총 또는 등가 저항 RT는 두 저항의 수학적 합이 됩니다. 즉, R1+R2가 됩니다. 세 개 이상의 불균형 (또는 동일한) 저항이 직렬로 연결된 경우 등가 저항은 R1+R2+R3+… 등이 됩니다.
저항이 직렬 회로에서 연결되는 경우 항상 중요한 점은 수학이 올바른지 확인하는 것입니다.
직렬로 연결된 두 개 이상의 저항의 총 저항 RT은 항상 연결된 체인에서 가장 큰 저항의 값보다 크게 됩니다.
위의 예시에서 RT=9kΩ이지만, 가장 큰 값의 저항은 단지 6kΩ입니다.
2-3) 직렬 저항 회로 예제
아래와 같은 직렬 회로가 있다고 하면,
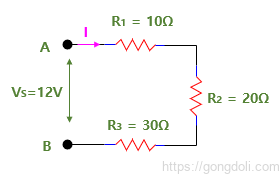
직렬 회로에서 각 저항에 대한 등가 저항, 직렬 전류, 전압 강하 및 전력을 계산한 결과입니다.
| 저항 (Resistance) | 전류 (Current) | 전압 (Voltage) | 전력 (Power) |
|---|---|---|---|
| R1 = 10Ω | I1 = 200mA | V1 = 2V | P1 = 0.4W |
| R2 = 20Ω | I2 = 200mA | V2 = 4V | P1 = 0.8W |
| R3 = 30Ω | I3 = 200mA | V3 = 6V | P1 = 1.2W |
| RT = 60Ω | IT = 200mA | VS = 12V | PT = 2.4W |
위의 회로에서 RT=60Ω, IT=200mA, VS=12V 및 PT=2.4W임을 확인할 수 있습니다.
3. 병렬 저항의 이해
직렬 및 병렬 저항 계산에서 병렬 저항 연결은 회로 전류가 여러 경로를 통해 흐를 수 있기 때문에 회로 전류는 하나의 경로로 제한되지 않습니다.
따라서 병렬 회로의 저항은 전류 분배기로 분류됩니다.
여러 경로가 제공되기 때문에 공급 전류가 흐를 수 있는데, 병렬 연결의 모든 분기에서 전류가 동일하지 않을 수 있습니다.
그러나 병렬 저항 네트워크의 모든 저항에 걸리는 전압 강하는 동일합니다.
따라서 병렬로 연결된 저항은 공통 전압을 가지며, 이는 모든 병렬로 연결된 요소에 대해 참입니다.
따라서 병렬 저항 회로는 두 점(또는 노드)에 연결된 저항으로 정의되며, 공통 전압원에 연결된 여러 전류 경로를 가지고 있음을 알 수 있습니다.
그런 다음 아래 병렬 저항 예에서 저항 R1, R2 및 R3은 모두 표시된 두 지점 A와 B 사이에 병렬로 연결됩니다.
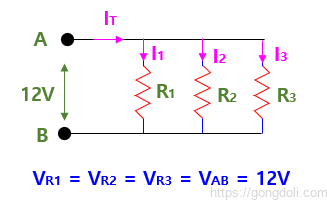
3-1) 병렬 저항 회로
직렬 및 병렬 저항 계산에서 이전의 직렬 저항 연결에서는 회로의 총 저항인 RT가 모든 개별 저항을 합한 값과 같음을 알았습니다.
병렬 저항의 경우 등가 회로 저항 RT는 다르게 계산됩니다.
여기서는 개별 저항의 역수 (1/R) 값이 저항 자체가 아닌 모두 함께 더해집니다.
이를 통해 등가 저항을 구할 수 있습니다.
3-2) 병렬 저항 등가 회로
직렬 및 병렬 저항 계산에서 여러 개의 저항이 병렬로 연결된 경우 등가 저항의 역수는 개별 저항의 역수들의 대수적 합입니다.
병렬로 연결된 두 저항 또는 임피던스가 같고 동일한 값을 가진 경우, 총 등가 저항 RT는 한 저항의 값의 반입니다.
이는 R/2로 같으며, 세 개의 동일한 저항이 병렬로 연결된 경우, R/3이 됩니다.
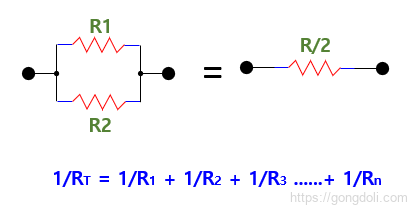
등가 저항은 항상 병렬 네트워크에서 가장 작은 저항보다 작습니다.
따라서 총 저항 RT는 병렬 저항이 추가됨에 따라 항상 감소합니다.
병렬 저항은 전도도(Conductance)라고 하는 값으로 제공되며, 기호 G이며 전도도의 단위는 시멘스(Siemens)입니다.
전도도는 저항의 역수 또는 역수입니다 (G = 1/R).
전도도를 다시 저항 값으로 변환하려면 전도도의 역수를 취해야하며, 이를 통해 병렬 저항의 총 저항 RT를 얻을 수 있습니다.
이제 같은 두 점 사이에 연결된 저항기가 병렬로 연결된다는 것을 알게 되었습니다.
그러나 병렬 저항 회로는 위에 제시된 형태 이외에도 여러 형태를 가질 수 있습니다.
3-3) 다양한 병렬 저항 연결
아래의 저항 연결는 서로 다르게 보일 수 있지만 모두 병렬로 저항기로 배열되어 있으므로 동일한 조건과 방정식이 적용됩니다.
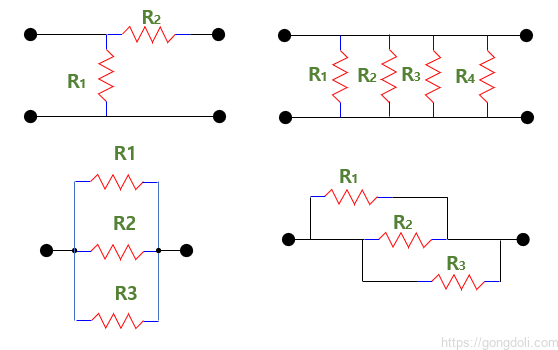
3-4) 병렬 저항 예제
다음과 같이 병렬 회로에 연결된 저항들의 총 저항인 RT를 찾을 수 있습니다.
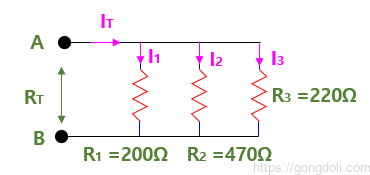
저항기가 병렬로 연결된 경우, 두 단자 A와 B 간의 총 저항 RT는 아래와 같이 계산됩니다

저항 값이 서로 다른 경우에도 이러한 역수 계산 방법은 하나의 병렬 네트워크 내에서 연결된 개별 저항의 모든 수를 계산하는 데 사용될 수 있습니다.
그러나 만약 병렬로 연결된 저항이 두 개뿐이라면, 총 또는 등가 저항 값인 RT를 더 간단하고 빠르게 찾기 위해 역수 계산을 조금 줄일 수 있는 더 간단한 공식을 사용할 수 있습니다.
두 개의 저항이 병렬로 연결된 경우, 동일한 값이거나 다른 값을 가지는 경우에도 총 저항 값을 찾는 더 간단한 곱-합산 방법은 다음과 같습니다
RT=(R1×R2)/(R1+R2)
4. 직렬 및 병렬 저항 계산 예제
4-1) 직렬 및 병렬 저항 계산 예제
직렬 및 병렬 저항 계산의 예를 들어, 다음 회로에서 12V 공급원에서 총 전류 (IT)를 계산해 보겠습니다.
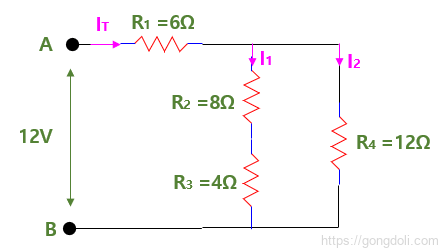
처음에는 이것이 어려운 것처럼 보일 수 있지만, 조금 더 자세히 살펴보면 R2와 R3 두 저항이 실제로 “직렬” 조합으로 연결되어 있음을 알 수 있습니다.
따라서 직렬 저항에서와 같이 이들을 더하여 등가 저항을 생성할 수 있습니다.
즉, 이 조합의 결과 저항은 다음과 같습니다.
R2 + R3 = 8Ω + 4Ω = 12Ω
따라서 R2와 R3 위의 두 저항을 12Ω의 저항 하나로 대체할 수 있습니다.
따라서 우리의 회로에는 이제 저항 R4와 “병렬”로 연결된 저항 RA가 있습니다.
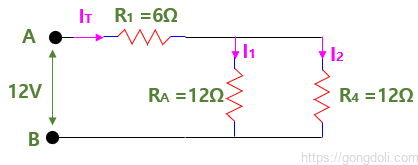
병렬 저항 공식을 사용하여이 병렬 조합을 하나의 등가 저항 값인 R(조합)으로 줄일 수 있습니다.
두 병렬 저항에 대한 공식은 다음과 같습니다.
Req=1/RA+1/R4=1/12+1/12=0.1667Ω
RT = 1/Req = 1/0.1667 = 6Ω
*. RT=(RA*R4)/(RA+R4) = (12*12)/(12+12) = 6Ω
따라서 직렬 및 병렬 저항 계산의 결과적인 저항 회로는 다음과 같습니다.
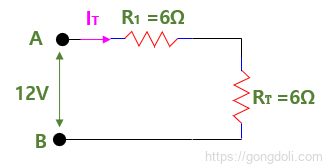
나머지 두 저항인 R1과 RT은 “직렬” 조합으로 연결되어 있으며 다시 직렬에 있는 저항을 더하여 (시리즈 저항) 점 A와 B 사이의 총 회로 저항은 다음과 같이 주어집니다.
즉, 직렬 및 병렬 저항 계산은
RAB = RT + R1 = 6Ω + 6Ω = 12Ω
