Contents
1. 키르히호프의 법칙(Kirchhoffs Circuit Law)이란?
키르히호프의 회로 법칙은 전기 회로에서 전압과 전류의 관계를 설명하는 중요한 법칙 중 하나입니다.
이 법칙은 헤르만 키르히호프가 발견했으며, 전기 회로에서 전압 및 전류의 유지를 설명합니다.
키르히호프의 회로 법칙에는 두 가지가 있습니다. 하나는 “전압 법칙”이고, 다른 하나는 “전류 법칙”입니다.
전압 법칙 (Kirchhoff’s Voltage Law, KVL)은 닫힌 회로의 모든 루프에 따라 적용됩니다.
이 법칙에 따르면 어떤 닫힌 경로를 따라 이동할 때, 전압의 총합은 항상 0이 됩니다.
다시 말해, 전기 회로의 모든 경로를 따라 이동하면 전압의 증가와 감소는 항상 상쇄되어야 합니다.
전류 법칙 (Kirchhoff’s Current Law, KCL)은 노드(접점)에 적용됩니다.
이 법칙에 따르면 어떤 노드에서 나가는 전류의 총합은 그 노드로 들어오는 전류의 총합과 같아야 합니다.
즉, 노드에서 전류는 보존됩니다.
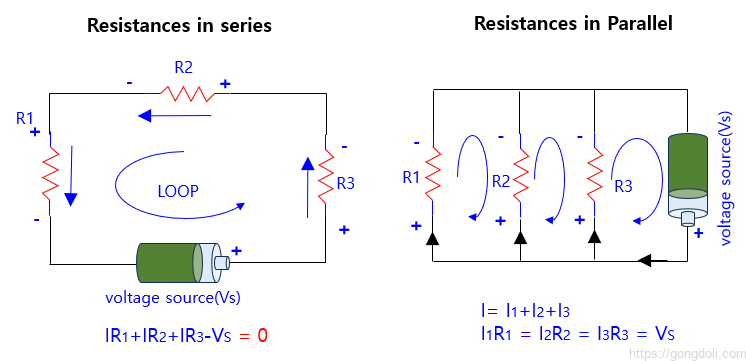
저항에 대한(연관 참조 : 직렬 및 병렬 저항 계산)것과 같이, 두 개 이상의 저항이 직렬, 병렬 또는 그 조합으로 연결되어 있는 경우 등가 저항( RT )을 찾을 수 있으며, 이러한 회로는 오옴의 법칙을 따릅니다.
그러나 가끔은 브릿지나 T 연결과 같은 복잡한 회로에서 오옴의 법칙만으로 회로 내의 전압이나 전류를 찾을 수 없는 경우가 있습니다.
이러한 유형의 계산에는 회로 방정식을 얻기 위한 특정한 규칙이 필요하며, 이를 위해 키르히호프의 회로 법칙을 사용할 수 있습니다.
1845년 독일 물리학자인 구스타프 키르히호프는 전기 회로 내에서 전류와 에너지의 보존에 관련된 두 가지 법칙 또는 규칙을 개발했습니다.
이 두 규칙은 보통 키르히호프의 회로 법칙으로 알려져 있으며, 하나는 폐회로 내에서 흐르는 전류를 다루는 것인 키르히호프의 전류 법칙(KCL)이고, 다른 하나는 폐회로 내에 있는 전압원을 다루는 것인 키르히호프의 전압 법칙(KVL)입니다.
- 연관 참조 : 직렬 및 병렬 저항 계산, 직렬 저항 예제, 병렬 저항 예제, 직병렬 저항 예제
- 연관 참조 : 오옴의 법칙 원리, 개념, 예제로 이해하기,전력 구하기,파이 차트
- 연관 참조 : 메쉬 전류 분석,Mesh Current Analysis,예제, 장점 3가지, 다른 분석과 비교
- 연관 참조 : 노드 전압 분석, 분석 방법 5단계, 예제, 메쉬 전류 분석과 비교
- 연관 참조 : 테브난의 정리, 5단계 방법, 예제, 한계와 주의 사항
- 연관 참조 : 노턴의 등가 회로, 정의, 분석 6단계, 예제, 한계와 주의 사항
- 연관 참조 : 밀만의 정리, 등가 회로, 예제,옴의 법칙과 키르히호프 법칙과 비교,한계
- 연관 참조 : 와이 델타 변환,Y-Δ 변환과 Δ-Y 변환, 변환 방정식, 예제 3개,활용
2. 키르히호프의 회로 법칙(Kirchhoffs Circuit Law) – KCL
키르히호프의 전류 법칙(KCL) 또는 KCL은 “접점 또는 노드에 들어오는 총 전류 또는 전하는 노드를 떠나는 전하와 정확히 같으므로 노드 내에서 전하가 손실되지 않는다”라고 말합니다.
다시 말해, 노드에 들어오고 나가는 모든 전류의 대수적 합은 0과 같아야 합니다.
즉, I(나가는) + I(들어오는) = 0이 되어야 합니다.
이러한 개념은 키르히호프에 의해 제안된 것으로 전하의 보존이라고도 합니다.
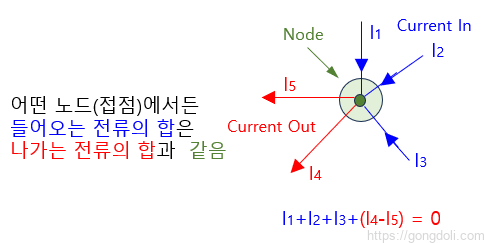
전류가 노드로 들어오고 나가는 경우를 예로 들면, 노드에 들어오는 세 개의 전류 I1, I2, I3은 모두 양수입니다.
반면 노드에서 나가는 두 개의 전류 I4와 I5는 음수입니다.
따라서 이를 다음과 같이 표현할 수 있습니다.
I1 + I2 + I3 – I4 – I5 = 0
전기 회로에서 “노드”는 케이블 및 구성 요소와 같은 두 개 이상의 전류를 운반하는 경로나 요소의 연결점 또는 교차점을 일반적으로 가리킵니다.
노드로 전류가 흐르려면 닫힌 회로 경로가 존재해야 합니다.
병렬 회로를 분석할 때 키르히호프의 전류 법칙을 사용할 수 있습니다.
3. 키르히호프의 회로 법칙(Kirchhoffs Circuit Law) – KVL
키르히호프의 전압 법칙(Kirchhoff’s Voltage Law, KVL)은 “전압 원본에 의해 구동되는 닫힌 회로 연결 내에서, 회로 루프 주변의 총 전압은 동일한 루프 내의 모든 전압 감소의 합과 같으며, 이 값은 0이다”라고 설명됩니다.
다시 말해, 닫힌 회로 내의 모든 전압 소스와 전압 감소의 대수적 합은 0이어야 합니다.
전압 감소의 대수적 합이 전압 소스의 대수적 합과 같음을 의미합니다.
이러한 개념은 키르히호프의 에너지 보존의 법칙으로 알려져 있습니다.
전압 법칙을 이해하기 위해서는 회로를 따라서 시작점에서 출발하여 같은 방향으로 계속 이동하면서 모든 전압 감소의 방향을 주의 깊게 살펴봐야 합니다.
이동한 후에는 다시 시작점으로 돌아와야 합니다. 시계 방향이나 반시계 방향을 유지하는 것이 중요하며, 그렇지 않으면 최종 전압 합이 0이 되지 않을 수 있습니다.
직렬 회로를 분석할 때 키르히호프의 전압 법칙을 사용할 수 있습니다.
키르히호프의 회로 법칙을 사용하여 DC 회로 또는 AC 회로를 분석할 때 회로의 부분을 설명하는 데 사용되는 여러 정의 및 용어가 있습니다.
이러한 용어는 회로 분석에서 자주 사용되므로 이해하는 것이 중요합니다.
회로 분석에서 노드, 경로, 가지, 루프 및 메쉬와 같은 용어가 자주 사용됩니다.
★ 일반적인 DC 회로 관련 용어
- 회로 – 회로는 전기 전류가 흐르는 닫힌 루프 전도 경로입니다.
- 경로 – 연결 요소나 원본의 단일 선로입니다.
- 노드 – 노드는 두 개 이상의 회로 요소가 연결되거나 결합되어 서로 연결되는 회로 내의 접점, 연결 또는 단자입니다. 노드는 점으로 표시됩니다.
- 가지 – 가지는 두 개의 노드 사이에 연결된 단일 또는 여러 구성 요소(저항기 또는 원본)입니다.
- 루프 – 루프는 회로 내에서 어떤 회로 요소나 노드도 두 번 이상 만나지 않는 간단한 닫힌 경로입니다.
- 메쉬 – 메쉬는 다른 경로가 없는 단일 닫힌 루프 시리즈 경로입니다. 메쉬 내에는 루프가 없습니다.
4. 키르히호프의 회로 법칙(Kirchhoffs Circuit Law) – 예제 풀이
40Ω 저항기 R3를 흐르는 전류(I3)를 구해보겠습니다.
회로에는 3개의 가지, 2개의 노드(A와 B) 및 2개의 독립적인 루프가 있습니다.
키르히호프의 전류 법칙(KCL)을 사용하여 방정식은
- 노드 A에서: I1 + I2 = I3
- 노드 B에서: I3 = I1 + I2
키르히호프의 전압 법칙(KVL)을 사용하여 루프는
- 루프 1은 10 = R1×I1 + R3×I3 = 10×I1 + 40×I3
- 루프 2은 20 = R2 ×I2 + R3× I3 = 20×I2 + 40×I3
- 루프 3은 10 – 20 = 10×I1 – 20×I2
I3는 I1 + I2의 합이므로 방정식을 다시 작성할 수 있습니다.
방정식 1 : 10 = 10×I1 + 40×(I1 + I2) = 50×I1 + 40×I2
방정식 2 : 20 = 20×I2 + 40×(I1 + I2) = 40×I1 + 60×I2
이제 우리는 뺄셈에 의해 줄어들 수 있는 두 “동시 방정식”을 가지고 있습니다.
이를 통해 I1과 I2의 값을 얻을 수 있습니다.
I2의 값으로 I1을 대체하면 I1의 값이 -0.143 A임을 얻을 수 있습니다.
I1의 값으로 I2를 대체하면 I2의 값이 +0.429 A임을 얻을 수 있습니다.
따라서 : I3 = I1 + I2
저항기 R3를 흐르는 전류는 다음과 같습니다
-0.143 + 0.429 = 0.286 A
및 저항기 R3에 걸리는 전압은 다음과 같습니다
0.286 x 40 = 11.44 V
I1에 대한 음수 부호는 초기에 선택한 전류 방향이 잘못되었음을 의미하지만, 여전히 유효합니다.
실제로 20V 배터리가 10V 배터리를 충전하고 있습니다.
5. KCL vs. KVL
| 특징 | KCL (키르히호프의 전류 법칙) | KVL (키르히호프의 전압 법칙) |
|---|---|---|
| 적용 대상 | 전류에 대한 법칙 | 전압에 대한 법칙 |
| 적용 방법 | 각 노드의 전류 합이 0이 되어야 함 | 닫힌 회로의 전압 합이 0이 되어야 함 |
| 적용 예시 | 병렬 분기에서 각 분기에 흐르는 전류 | 회로의 루프에서 전압 강하 및 상승 |
| 수식 | Σ(I_in) = Σ(I_out) | Σ(V_sources) = Σ(V_drops) |
| 유용성 및 활용 | 분기 회로 분석 및 노드에서 전류 계산 | 닫힌 회로의 전압 강하 및 상승 계산 |
| 회로 분석 | 복잡한 병렬 회로 분석에 유용 | 닫힌 회로의 전압 변화 및 흐름 분석 |
| 물리적 해석 | 전류의 대한 보존 법칙 | 에너지의 대한 보존 법칙 |
KCL은 노드에서의 전류의 합이 0이 되어야 한다는 점에 중점을 두며, KVL은 닫힌 회로에서의 전압의 합이 0이 되어야 한다는 점에 중점을 둡니다.
이러한 두 가지 법칙은 회로 분석에 있어서 중요한 개념이며, 각각의 특징에 따라 다른 종류의 회로 분석에 활용됩니다
6. 키르히호프의 회로 법칙(Kirchhoffs Circuit Law)적용과 한계
6-1) 키르히호프 회로 법칙의 적용
키르히호프의 회로 법칙은 회로의 구성과 구조에 관계 없이 모든 회로를 분석하는 데 적용할 수 있습니다.
이러한 법칙은 다양한 응용 분야에서 유용하게 활용됩니다.
- 알 수 없는 요소의 결정: 키르히호프의 법칙은 회로에서 알 수 없는 요소인 저항, 임피던스, 전압 및 전류(방향 및 값)를 결정하는 데 사용됩니다.
회로 내의 각 요소에 대한 전압과 전류를 계산하여 이러한 값을 찾을 수 있습니다. - 분기 회로 분석: 분기 회로에서 각 분기를 통과하는 전류는 모든 접합부에 키르히호프의 전류 법칙을 적용하여 결정됩니다.
각 접합부에서 전류의 합은 0이 되어야 합니다.
또한 각 루프에 키르히호프의 전압 법칙을 적용하여 회로의 전압을 결정할 수 있습니다. - 루프 회로 분석: 루프 회로에서 각 독립 루프를 통과하는 전류는 각 루프에 키르히호프의 전압 법칙을 적용하여 결정됩니다.
이를 통해 회로의 각 구성 요소에서 전류를 계산할 수 있습니다.
이러한 분석을 통해 회로의 전체 동작을 이해하고 최적화할 수 있습니다.
6-2) 키르히호프의 회로 법칙의 한계
- 복잡한 회로
많은 노드와 루프가 있는 복잡한 회로의 경우, 수백 개의 방정식이 필요할 수 있으며, 분석이 어려울 수 있습니다. - 비선형 회로
회로의 구성 요소가 비선형 요소(다이오드, 트랜지스터 등)로 이루어진 경우, 키르히호프의 법칙이 정확하지 않을 수 있습니다. - 위상 및 주파수 응답
키르히호프의 회로 법칙은 DC(직류) 및 저주파수 AC(교류) 회로에 대해 적용되지만, 고주파 AC 회로에 대해서는 정확하지 않을 수 있습니다.
키르히호프의 회로 법칙은 대부분의 기본적인 전기 회로에서 유용하지만, 대규모 및 복잡한 회로에서는 다른 방법과 함께 사용되어야 합니다.