Contents
1. 개요
키르히호프 회로 법칙, 메쉬 전류 분석, 그리고 노드 전압 분석을 사용하여 복잡한 전기 회로를 해결하는 방법이 있습니다.
키르히호프의 다음으로 가장 흔히 사용되는 회로 분석 이론 중 하나인 테브난의 정리에 대해 살펴보겠습니다.
테브난의 정리는 “여러 전압과 저항을 포함하는 선형 회로는 하나의 전압과 하나의 저항으로만 구성된 등가 회로로 대체될 수 있다”고 말합니다.
다시 말해, 어떤 회로든 얼마나 복잡하더라도, 단 하나의 일정한 전압 소스가 연결된 저항(또는 임피던스)과 부하에 연결된 하나의 저항으로만 구성된 등가 이차 회로로 단순화할 수 있습니다.
즉, 테브난의 정리는 복잡한 회로를 간단한 등가 회로로 대체하여 회로 분석을 용이하게 만듭니다.
이를 통해 우리는 전력 시스템 및 다른 연결된 회로의 동작을 더 잘 이해하고 예측할 수 있습니다
다만, 테브난의 회로 정리는 전류와 전압의 관점에서 수학적으로 설명될 수 있지만, 큰 네트워크에서는 메쉬 전류 분석 또는 노드 전압 분석만큼 강력하지 않습니다.
왜냐하면 테브난 연습에서는 일반적으로 메쉬 또는 노드 전압 분석을 사용해야 하기 때문에, 처음부터 사용하는 것이 좋습니다.
그러나 트랜지스터, 전압 Source(예: 배터리) 등의 테브난의 등가 회로는 회로 설계에 매우 유용합니다.
- 연관 참조 : 키르히호프의 회로 법칙, KCL, KVL, 예제, KCL vs. KVL,적용과 한계
- 연관 참조 : 오옴의 법칙 원리, 개념, 예제로 이해하기,전력 구하기,파이 차트
- 연관 참조 : 메쉬 전류 분석,Mesh Current Analysis,예제, 장점 3가지, 다른 분석과 비교
- 연관 참조 : 노드 전압 분석, 분석 방법 5단계, 예제, 메쉬 전류 분석과 비교
- 연관 참조 : 노턴의 등가 회로, 정의, 분석 6단계, 예제, 한계와 주의 사항
- 연관 참조 : 밀만의 정리, 등가 회로, 예제,옴의 법칙과 키르히호프 법칙과 비교,한계
- 연관 참조 : 와이 델타 변환,Y-Δ 변환과 Δ-Y 변환, 변환 방정식, 예제 3개,활용
2. 테브난의 정리 5단계
전기 회로에서 테브난의 정리를 적용할 때, 우리는 주어진 회로를 더 단순한 등가 회로로 대체할 수 있습니다.
이를 이해하기 위해 우리는 일련의 단계를 따를 것입니다.
- source 회로 분석: 우선, 우리는 source 회로를 분석합니다.
이것은 다양한 전압과 저항으로 구성된 복잡한 회로일 수 있습니다. - 등가 전압 계산: 다음으로, 등가 전압을 계산합니다.
등가 전압은 회로의 출력 단자 사이에서 나타나는 전압입니다.
이것은 회로의 전체 특성을 대표합니다. - 등가 저항 계산: 그 후, 등가 저항을 계산합니다.
등가 저항은 회로를 대체할 때 source 회로와 등가 회로가 동일한 출력을 제공하도록 하는데 중요합니다. - 등가 회로 구성: 마지막으로, 등가 전압과 등가 저항을 사용하여 등가 회로를 구성합니다.
이 등가 회로는 source 회로와 동등한 동작을 합니다.
3. 테브난의 정리 예제
테브난의 정리는 복잡한 전기 회로를 단순한 등가 회로로 대체하여 회로 분석을 용이하게 만드는 이론입니다.
이를 통해 우리는 복잡한 회로를 단순화하여 전압 및 전류를 쉽게 계산할 수 있습니다.
예를 들어,
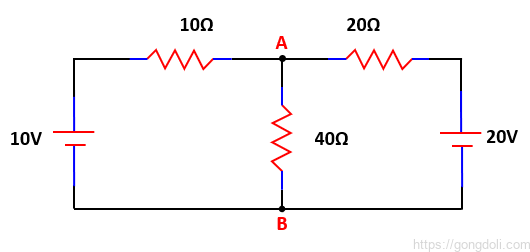
3-1) source 회로 분석
먼저, 회로를 분석하기 위해 단자 A-B에 연결된 중심 40Ω 부하 저항을 제거하고, 전압 source에 연관된 모든 내부 저항을 제거해야 합니다.
이를 위해 회로에 연결된 모든 전압 source을 단락시키고, 즉 v = 0으로 만들거나, 회로에 연결된 모든 전류 source을 Open시켜 i = 0으로 만듭니다.
이렇게 하는 이유는 회로 분석을 위해 이상적인 전압 source 또는 이상적인 전류 source을 가지기를 원하기 때문입니다.
등가 저항 Rs의 값은 모든 전압 source이 단락된 상태에서 단자 A와 B로부터 바라볼 때의 총 저항을 계산하여 얻습니다.
그러면 다음과 같은 회로를 얻을 수 있습니다.
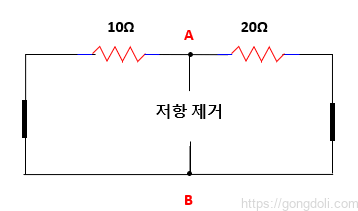
3-2) 등가 저항 계산(Rs)
전압 Vs는 단자 A와 단자 B 사이에 개방 회로가 있을 때 전체 전압으로 정의됩니다.
부하 저항 RL이 연결되지 않은 상태입니다.
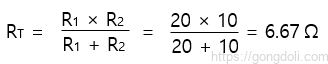
3-3) 등가 전압 계산(Vs)
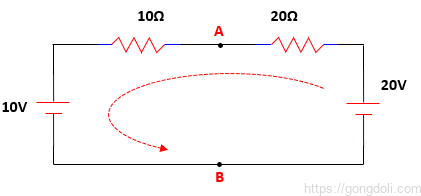
이제 두 전압을 회로에 다시 연결해야 하며 VS = VAB로서 루프 주변에 흐르는 전류는
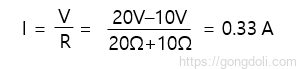
이 전류는 0.33 A(330mA)로 두 저항 모두에 공통되므로 20Ω 저항 또는 10Ω 저항에 걸친 전압 강하는

즉, 테브난의 등가 회로는 6.67Ω의 직렬 저항과 13.33v의 전압원으로 구성됩니다.
3-4) 등가 회로 구성
40Ω 저항을 회로에 다시 연결하면
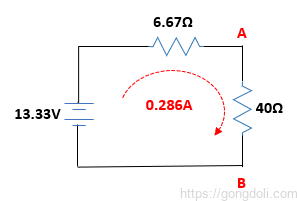
이를 통해 회로 주변에 흐르는 전류는
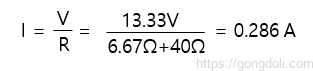
4. 테브난의 정리 한계와 주의 사항
테브난의 정리는 전기 회로를 간단한 등가 회로로 대체하여 분석을 용이하게 만드는 강력한 도구입니다.
그러나 테브난의 정리를 적용할 때 주의해야 할 몇 가지 한계와 제약 사항이 있습니다.
테브난 정리의 한계와 주의사항
- 비선형 회로: 테브난 정리는 선형 회로에만 적용됩니다.
비선형 요소가 있는 경우에는 적용할 수 없습니다. - 시간에 따른 변화: 테브난 정리는 정상 상태에서만 유효합니다.
시간에 따라 변하는 회로나 주파수 응답 등의 동적인 특성은 고려되지 않습니다. - 주파수 응답: 고주파 회로나 높은 주파수에서는 회로의 용량이나 인덕턴스가 중요한 역할을 할 수 있습니다.
이러한 경우에는 테브난 정리가 적용되지 않을 수 있습니다. - 근거리 효과: 회로의 크기가 작거나, 저항 값이 극히 작은 경우에는 회로의 근거리 효과가 무시될 수 있습니다.
이러한 경우에는 테브난 정리를 적용하기 어려울 수 있습니다. - 복잡한 회로 구성: 테브난 정리는 단순한 회로 구성에서 가장 잘 작동합니다.
복잡한 회로 구성에서는 적용이 제한될 수 있으며, 메쉬 분석이나 노달 분석과 같은 다른 회로 분석 기법이 필요할 수 있습니다.
이러한 한계와 제약 사항을 고려하여 테브난 정리를 적용할 때에는 주의가 필요합니다.
적절한 상황에서 테브난 정리를 사용하면 회로 분석을 간편하게 할 수 있지만, 그렇지 않은 경우에는 다른 회로 분석 방법을 고려해야 합니다.
