1. 16진수 (hexadecimal)란 무엇인가?
16진수 (Hexadecimal)는 숫자를 표현하기 위해 16개의 기호를 사용하는 숫자 체계입니다.
16진수는 컴퓨터 과학 및 디지털 전자공학에서 중요한 역할을 하며, 주로 메모리 주소, 색상 코드, 머신 코드 등에서 사용됩니다.
16진수는 0에서 9까지의 숫자와 A에서 F까지의 알파벳을 사용하여 숫자를 표현합니다.
여기서 A는 10, B는 11, C는 12, D는 13, E는 14, F는 15를 나타냅니다.
예를 들어, 16진수 1A는 10진수로 26을 의미합니다.
16진수, 또는 헥사데시멀(Hexadecimal) 숫자 체계는 비교적 최근에 발명된 것입니다.
다른 고대 숫자 체계와 달리, 16진수는 컴퓨터 과학과 디지털 전자공학의 발달과 함께 등장했습니다.
16진수 (hexadecimal)의 기원은 20세기 중반으로 거슬러 올라갑니다.
컴퓨터가 개발되면서, 데이터와 명령어를 효율적으로 표현하고 조작할 필요성이 생겼습니다.
초기의 컴퓨터는 2진수(0과 1)를 사용하여 데이터를 처리했지만, 긴 2진수 문자열을 다루는 것은 어렵고 오류가 발생하기 쉬웠습니다.
이에 따라 더 짧고 간결한 방법으로 데이터를 표현할 수 있는 16진수가 도입되었습니다.
16진수 (hexadecimal)는 각 자리에서 4개의 이진수 비트를 사용하여 숫자를 표현할 수 있습니다.
즉, 4비트는 16가지의 서로 다른 값을 가질 수 있으며, 이는 0부터 15까지의 숫자로 표현됩니다.
이 때문에 16진수는 2진수와 자연스럽게 연결되며, 컴퓨터 시스템에서 매우 유용하게 사용됩니다.
- 연관 참조 : 이진수(Binary) 란?, 표기, 구조, 이진수 변환, 덧셈, 뺄셈, 곱셈, 나눗셈 연산, 예제, 컴퓨터
- 연관 참조 : 8진수_octal, 십진수 & 2진수로 변환, 8진수 연산,예제
- 연관 참조 : 2진수 사칙 연산 계산기, Binary calculator, 사용 방법
- 연관 참조 : 8진수 사칙 연산 계산기, Hexadecimal calculator, 사용 방법
2. 16진수 (hexadecimal) 표기법과 구조
2-1) 16진수의 기본 구조
16진수 (Hexadecimal)는 16개의 기호를 사용하는 숫자 체계입니다.
각 자리는 0부터 15까지의 값을 가질 수 있으며, 이를 표현하기 위해 0부터 9까지의 숫자와 A부터 F까지의 알파벳이 사용됩니다.
다음 표는 16진수의 각 기호와 그에 대응하는 10진수 값을 보여줍니다.
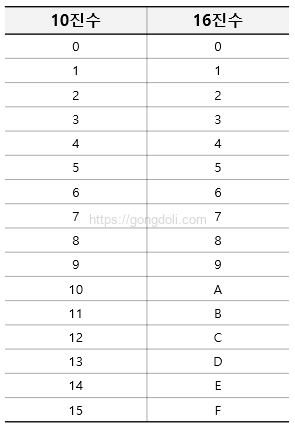
16진수는 자리 값의 가중치가 16의 거듭제곱으로 증가합니다.
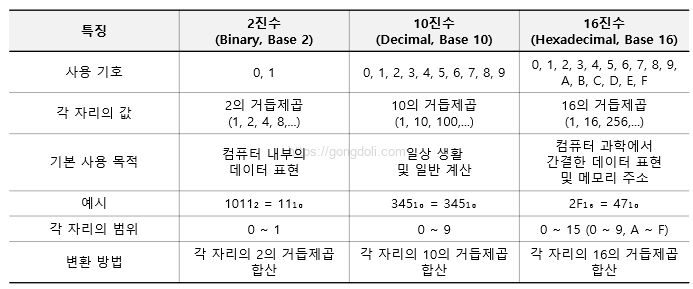
2-2) 16진수와 다른 진법(2진수, 10진수)과의 차이점
2-2-1) 2진수에서 10진수로 변환
2진수 1011을 10진수로 변환해 보겠습니다.
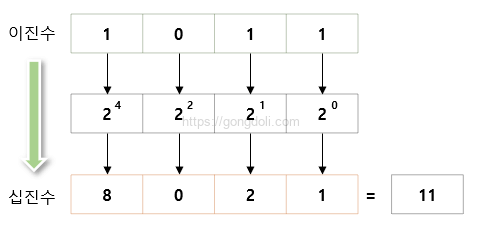
즉, 100112=1110
10진수 11을 2진수로 다시 변환하면
1110=10112
2-2-2) 16진수에서 10진수로 변환
16진수 2F를 10진수로 변환해 보겠습니다.
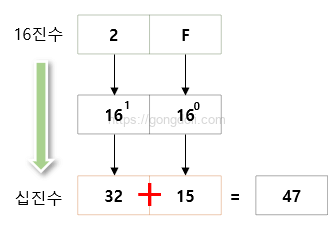
10진수에서 16진수로 다시 변환하면
4710 = 47/16 = 2𝐹16
2-3) 16진수의 기호 및 표기 방식
16진수 (hexadecimal)는 일반적으로 숫자 앞에 “0x” 또는 “0X”를 붙여 표기합니다.
이는 다른 진법과 구분하기 위해 사용됩니다.
예를 들어, 10진수 255는 16진수로 변환하면 0xFF로 표기됩니다.
이 표기 방식은 프로그래밍 언어에서 특히 많이 사용됩니다.
예를 들어 C언어에서의 사용하는 경우에는
int num = 0x1A3; // 16진수 1A3를 변수에 저장웹 디자인에서의 사용하는 경우에는
<p style="color: #FF5733;">이 텍스트는 주황색입니다.</p>여기서 #FF5733은 16진수로 표현된 색상 코드로, 각각 빨강, 초록, 파랑(RGB) 성분을 나타냅니다.
16진수 (hexadecimal)는 컴퓨터 과학과 디지털 전자공학에서 중요한 숫자 체계로, 0에서 15까지의 값을 표현하기 위해 0-9와 A-F의 기호를 사용합니다.
2진수, 10진수와 비교하여 더 간결하고 효율적인 데이터 표현을 제공하며, 주로 메모리 주소, 색상 코드, 디버깅 정보 등에 사용됩니다.
16진수 (hexadecimal)는 일반적으로 “0x” 또는 “0X”를 앞에 붙여 다른 진법과 구분합니다.
3. 16진수/10진수/2진수 변환 예제
3-1) 16진수↔10진수 변환 방법
3-1-1) 16진수를 10진수로 변환하는 방법
16진수 (hexadecimal)를 10진수로 변환하는 방법은 각 자리의 값을 16의 거듭제곱과 곱한 후, 이를 모두 합산하는 것입니다.
예를 들어 16진수 2F3를 10진수로 변환해 보겠습니다.
각 자리의 값을 10진수로 변환하면
2= 2
F=15
3=3
각 자리의 값을 16의 거듭제곱과 곱하면
2 × 16² = 2 × 256 = 512
F × 16¹ = 15 × 16 = 240
3 × 16⁰ = 3 × 1 = 3
모두 합산하면
512 + 240 + 3 = 755
따라서 16진수 2F3는 10진수로 755입니다.
3-1-2) 10진수를 16진수로 변환하는 방법
10진수를 16진수 (hexadecimal)로 변환하는 방법은 16으로 나누고, 나머지를 구하는 과정을 반복하는 것입니다.
예를 들어, 10진수 755를 16진수로 변환해 보겠습니다.
755를 16으로 나누고 나머지를 구하면
755 ÷ 16 = 47, 나머지 3
몫 47을 16으로 나누고 나머지를 구하면
47 ÷ 16 = 2, 나머지 15 (F)
몫 2를 16으로 나누고 나머지를 구하면
2 ÷ 16 = 0, 나머지 2
나머지를 역순으로 배열하면
2F3
따라서 10진수 755는 16진수로 2F3입니다.
3-2) 16진수↔2진수 변환 방법
3-2-1) 16진수를 2진수로 변환하는 방법
16진수 (hexadecimal)를 2진수로 변환하는 방법은 각 16진수 자리를 4비트의 2진수로 변환하는 것입니다.
예를 들어, 16진수 2F3를 2진수로 변환해 보겠습니다.
각 자리의 16진수 (hexadecimal)를 2진수로 변환하면
2: 0010
F: 1111
3: 0011
각 4비트 2진수를 나열하면
0010 1111 0011
따라서 16진수 2F3는 2진수로 0010 1111 0011입니다.
3-2-2) 2진수를 16진수로 변환하는 방법
2진수를 16진수 (hexadecimal)로 변환하는 방법은 4비트씩 묶어서 각각을 16진수로 변환하는 것입니다.
예를 들어, 2진수 0010 1111 0011를 16진수로 변환해 보겠습니다.
4비트씩 묶으면
0010, 1111, 0011
각 묶음을 16진수로 변환하면
0010: 2
1111: F
0011: 3
따라서 2진수 0010 1111 0011는 16진수 (hexadecimal)로 2F3입니다.
4. 16진수 연산
4-1) 16진수 덧셈
16진수 (hexadecimal) 덧셈은 10진수 덧셈과 유사하지만, 각 자리의 합이 16을 초과할 경우 자리 올림이 발생합니다.
예를 들어,16진수 1A3 + 2F5을 계산해 보겠습니다.
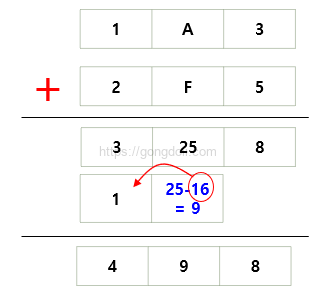
- 각 자리의 값을 더함
가장 오른쪽 자리: 3 + 5 = 8
가운데 자리: A (10) + F (15) = 25 (1 올림, 25 – 16 = 9)
가장 왼쪽 자리: 1 + 2 + 1(올림) = 4 - 결과
1A3 + 2F5 = 498
따라서 16진수 1A3와 2F5를 더한 결과는 498입니다.
4-2) 16진수 뺄셈
16진수 (hexadecimal) 뺄셈은 10진수 뺄셈과 유사하지만, 각 자리에서 빌림이 필요할 경우 16진수 (hexadecimal)의 값을 빌려옵니다.
예를 들어, 16진수 3B2 – 1A4 를 계산해 보겠습니다.
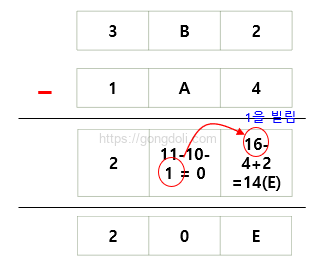
- 각 자리의 값을 뺌
가장 오른쪽 자리: 2 – 4 = -2 (1 빌림, 2 + 16 – 4 = 14 (E))
가운데 자리: B (11) – A (10) – 1 (빌림) = 0
가장 왼쪽 자리: 3 – 1 = 2 - 결과
3B2 – 1A4 = 20E
따라서 16진수 3B2에서 1A4를 뺀 결과는 20E입니다.
4-3) 16진수 곱셈
16진수 (hexadecimal) 곱셈은 각 자리를 곱하고 자리 올림을 처리하는 방식입니다.
예를 들어, 16진수 2A × 3을 계산해 보겠습니다.
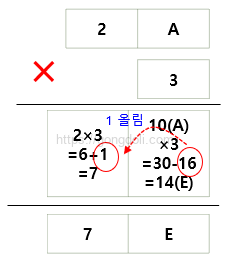
- 각 자리의 값을 곱함
A (10) * 3 = 30 (1 올림, 30 – 16 = 14 (E))
2 * 3 + 1 (올림) = 7 - 결과
2A * 3 = 7E
따라서 16진수 2A와 3을 곱한 결과는 7E입니다.
4-4) 16진수 나눗셈
16진수 (hexadecimal) 나눗셈은 10진수 나눗셈과 유사하게 나눗셈을 수행하고 나머지를 계산하는 과정입니다.
예를 들어, 16진수 7D ÷ 5를 계산해 보겠습니다.
16진수 7D를 10진수로 변환하면
7D₁₆ = 7 × 16¹ + D × 16⁰
D는 16진수에서 13에 해당하므로,
7 × 16 + 13 = 112 + 13 = 125₁₀
10진수 125를 10진수 5로 나누면
125 ÷ 5 = 25 (몫), 나머지 0
몫을 16진수 (hexadecimal)로 변환하면
25₁₀ = 19₁₆ (10진수 25를 16진수로 변환하는 방법은 아래 참조)25를 16으로 나누면 됩니다.
- 25 ÷ 16 = 1, 나머지 9
- 따라서 25₁₀ = 19₁₆
- 나머지를 16진수로 변환하면
- 나머지 0은 그대로 16진수 0
즉, 결과는
- 7D₁₆ ÷ 5₁₆ = 19₁₆, 나머지 0
따라서 16진수 (hexadecimal) 7D를 5로 나눈 결과는 몫이 19, 나머지가 0입니다.