Contents
1. 8진수(octal)란 무엇인가?
8진수_octal는 컴퓨터 과학과 디지털 시스템에서 사용되는 수 체계 중 하나로, 0에서 7까지의 숫자를 사용하여 값을 표현합니다.
8진수는 2진수나 16진수와 같이 컴퓨터 시스템에서 데이터를 효율적으로 처리하고 표현하는 데 중요한 역할을 합니다.
8진수_octal는 기본적으로 8을 기수(base)로 하는 수 체계입니다.
이는 0에서 7까지의 8가지 숫자를 사용하여 모든 수를 표현합니다.
8진수는 주로 컴퓨터 과학에서 간단하게 2진수(Binary)를 표현하는 데 사용되며, 특히 초기 컴퓨터 시스템과 프로그래밍에서 많이 사용되었습니다.
예를 들어, 10진수(Decimal) 8은 8진수로 10이며, 이는 1 * 8^1 + 0 * 8^0 = 8을 의미합니다.
8진수_octal 체계는 고대 문명에서도 그 기원을 찾을 수 있습니다.
특히, 8진수는 인간이 손가락을 사용하여 셈을 할 때 시작되었을 가능성이 큽니다.
사람들은 양 손을 모두 사용하여 10진법으로 숫자를 셀 수 있지만, 한 손의 손가락 8개를 이용하여 셈을 하는 방법이 8진법의 기원으로 여겨지기도 합니다.
또한, 바빌로니아와 같은 고대 문명에서도 8진수의 흔적이 발견됩니다.
바빌로니아인들은 60진법을 사용했으나, 그 안에서 부분적으로 8진수와 비슷한 체계를 사용했습니다.
컴퓨터 과학에서 8진수는 특히 초기 컴퓨터 시스템과 프로그래밍에서 매우 중요한 역할을 했습니다.
컴퓨터 내부에서 모든 데이터는 2진수로 표현됩니다.
하지만, 2진수는 자릿수가 너무 길어 읽기와 쓰기가 어렵기 때문에, 이를 더 간결하게 표현하기 위해 8진수가 사용되었습니다.
예를 들어, 2진수 11010100은 8진수로 324로 변환할 수 있습니다.
이렇게 변환하면 데이터의 표현이 더 간단해지고, 오류를 줄일 수 있습니다.
또한, 유닉스와 같은 운영 체제에서는 파일 권한을 설정할 때 8진수를 사용합니다.
파일 권한은 읽기, 쓰기, 실행의 세 가지 권한을 각각 3비트씩 사용하여 설정합니다.
이를 8진수로 표현하면, 한 자리 숫자(0부터 7)로 각 권한을 쉽게 나타낼 수 있습니다.
이러한 이유로 8진수(octal)는 컴퓨터 과학의 역사에서 중요한 위치를 차지하게 되었으며, 오늘날에도 특정 분야에서 여전히 사용되고 있습니다.
8진수는 2진수와 10진수 사이의 중간 다리 역할을 하며, 복잡한 이진 데이터를 보다 쉽게 다룰 수 있도록 도와줍니다.
- 연관 참조 : 이진수(Binary) 란?, 표기, 구조, 이진수 변환, 덧셈, 뺄셈, 곱셈, 나눗셈 연산, 예제, 컴퓨터
- 연관 참조 : 16진수 (hexadecimal),표기법과 구조,16진수↔10진수/2진수 변환 예제,16진수연산
- 연관 참조 : 2진수 사칙 연산 계산기, Binary calculator, 사용 방법
- 연관 참조 : 16진수 사칙 연산 계산기, hexadecimal calculator, 사용 방법
2. 8진수_octal의 표기법과 구조
2-1) 8진수의 기본 구조
8진수_octal는 0부터 7까지의 숫자를 사용하여 모든 수를 표현합니다.
즉, 각 자리에는 0, 1, 2, 3, 4, 5, 6, 7의 값만 올 수 있습니다.
8진수는 8을 기수(base)로 하며, 각 자리의 값은 8의 거듭제곱 배수로 계산됩니다.
예를 들어, 8진수 103를 10진수로 변환해 보겠습니다.
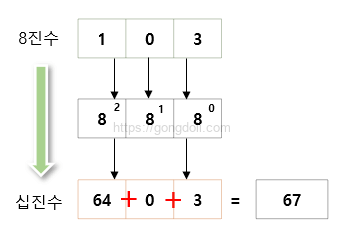
8진수 103에서 각 자리의 값: 1, 0, 3
자리의 위치에 따른 가중치: 8², 8¹, 8⁰
1 × 8² = 1 × 64 = 64
0 × 8¹ = 0 × 8 = 0
0 × 8⁰ = 3 × 1 = 3
합계: 64 + 0 + 3 = 67
따라서, 8진수 103는 10진수로 67입니다.
2-2) 8진수와 다른 진법(2진수, 10진수, 16진수)과의 차이점
8진수_octal는 2진수, 10진수, 16진수와 다음과 같은 차이점이 있습니다.
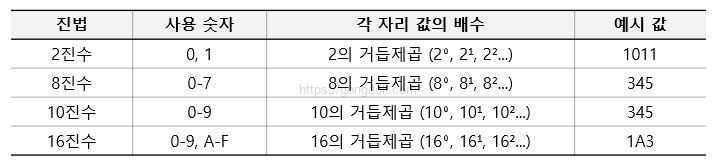
- 2진수 (Binary): 0과 1 두 개의 숫자만 사용합니다.
각 자리는 2의 거듭제곱 배수로 계산됩니다.
예를 들어, 2진수 1011은 10진수로 11입니다. - 8진수 (Octal): 0부터 7까지의 숫자를 사용합니다.
각 자리는 8의 거듭제곱 배수로 계산됩니다.
예를 들어, 8진수 345는 10진수로 229입니다. - 10진수 (Decimal): 0부터 9까지의 숫자를 사용합니다.
각 자리는 10의 거듭제곱 배수로 계산됩니다.
예를 들어, 10진수 345는 그대로 345입니다. - 16진수 (Hexadecimal): 0부터 9까지와 A부터 F까지의 숫자를 사용합니다.
A는 10, B는 11, C는 12, D는 13, E는 14, F는 15를 의미합니다.
각 자리는 16의 거듭제곱 배수로 계산됩니다.
예를 들어, 16진수 1A3은 10진수로 419입니다.
2-3) 8진수의 기호 및 표기 방식
8진수(octal)는 주로 컴퓨터 과학과 디지털 시스템에서 사용됩니다.
- 숫자 사용: 0부터 7까지의 숫자를 사용합니다.
예를 들어, 8진수 127은 유효한 8진수입니다. - 접두사 사용: 프로그래밍 언어에서 8진수를 표시할 때, 종종 접두사를 사용합니다.
예를 들어, Python에서는 0o 또는 0O를 접두사로 사용하여 8진수를 나타냅니다. (예: 0o127.) - 구분을 위한 표기: 10진수와 구분하기 위해, 종종 8진수는 8진수 또는 Octal이라고 명시합니다.
예를 들어, 8진수 123은 10진수로 1 × 8² + 2 × 8¹ + 3 × 8⁰ = 64 + 16 + 3 = 83입니다.
2진수 101100을 8진수로 변환하면 54입니다. (2진수를 3자리씩 묶어 계산: 101(5) 100(4))
이처럼, 8진수는 컴퓨터 시스템과 프로그래밍에서 중요한 역할을 하며, 데이터를 효율적으로 표현하고 처리하는 데 유용합니다.
이를 이해하고 활용하는 것은 디지털 시스템과 컴퓨터 과학을 배우는 데 필수적입니다.
3. 8진수_octal의 표기법과 구조
3-1) 8진수를 10진수로 변환하는 방법
8진수_octal를 10진수로 변환하는 방법은 각 자리 숫자에 8의 거듭 제곱을 곱한 후, 이를 모두 더하는 방식입니다.
예를 들어, 8진수 345를 10진수로 변환해 보겠습니다.
3 × 8² + 4 × 8¹ + 5 × 8⁰
3 × 64 + 4 × 8 + 5 × 1
192 + 32 + 5 = 229
즉, 8진수(octal) 345는 10진수로 229를 의미합니다.
3-2) 10진수를 8진수로 변환하는 방법
10진수를 8진수로 변환하는 방법은 10진수를 8로 나눠서 나머지를 구하고, 이를 역순으로 배열하는 방식입니다.
예를 들어, 10진수 229를 8진수로 변환해 보겠습니다.
먼저, 10진수 229를 8로 나누면
- 229 ÷ 8 = 28, 나머지 5
- 28 ÷ 8 = 3, 나머지 4
- 3 ÷ 8 = 0, 나머지 3
나머지를 역순으로 배열하면, 345가 나옵니다.
따라서, 10진수 229는 8진수로 345입니다.
3-3) 8진수를 2진수로 변환하는 방법
8진수_octal를 2진수로 변환하는 방법은 각 8진수 자리를 3자리의 2진수로 바꾸는 방식입니다.
각 8진수 숫자는 3자리의 2진수로 표현할 수 있기 때문입니다.
예를 들어, 8진수 345를 2진수로 변환해 보겠습니다.
8진수 각 자리의 2진수 변환
3 = 011
4 = 100
5 = 101
변환된 값을 순서대로 배열하면, “011 100 101”
따라서, 8진수 345는 2진수로 011100101입니다.
3-4) 2진수를 8진수로 변환하는 방법
2진수를 8진수_octal로 변환하는 방법은 2진수를 오른쪽에서부터 3자리씩 묶어서 각 묶음을 8진수로 바꾸는 방식입니다.
예를 들어, 2진수 011100101을 8진수로 변환해 보겠습니다.
2진수를 오른쪽에서부터 3자리씩 묶습니다.
011 100 101
각 묶음을 8진수로 변환하면
011 = 3
100 = 4
101 = 5
변환된 값을 순서대로 배열하면 345입니다.
따라서, 2진수 011100101은 8진수로 345입니다.
4. 8진수(octal) 연산
8진수_octal 연산은 10진수 연산과 유사하지만, 각 자리의 값이 8을 넘지 않는다는 점에서 차이가 있습니다.
4-1) 8진수 덧셈
8진수_octal 덧셈은 10진수 덧셈과 같은 방법으로 수행되지만, 각 자리의 값이 8 이상이면 자리 올림을 해야 합니다.
예를 들어, 8진수 345와 127을 더해보겠습니다.
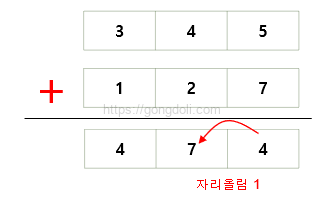
덧셈 과정을 해보면
5 + 7 = 12 (8진수로 14, 자리 올림 1)
4 + 2 + 1(자리 올림) = 7
3 + 1 = 4
따라서, 8진수 345와 127을 더한 결과는 474입니다.
4-2) 8진수 뺄셈
8진수_octal 뺄셈도 10진수 뺄셈과 유사하지만, 값이 0보다 작아질 때는 자리 내림을 해야 합니다.
예를 들어, 8진수 345에서 127을 빼보겠습니다.
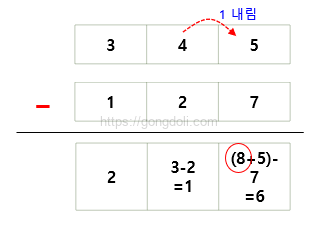
뺄셈 과정을 해보면
5 – 7는 불가능하므로 자리 내림
15(8 + 7) – 7 = 6 (자리 내림 1)
3 – 1(자리 내림) – 2 = 0
3 – 1 = 2
따라서, 8진수 345에서 127을 뺀 결과는 216입니다.
4-3) 8진수 곱셈
8진수_octal 곱셈은 각 자리 숫자를 곱한 후 자리를 맞춰 더하는 방식입니다.
예를 들어, 8진수 34와 12를 곱해보겠습니다.
곱셈 과정을 해보면
34 × 2 = 70 (10진수로 28)
>. 뒷자리 4×2=8(십진수)로 8진수로 나누면, 몫은 1, 나머지는 0
>. 앞자리 3×2=6(십진수)로 8진수로 나누면, 몫은 0, 나머지는 6(자리올림 1)
즉, 7(6+자리올림1)0(뒷자리나머지) = 70
34 × 1 = 34 (10진수로 28)
>. 뒷자리 4×1=4(십진수)로 8진수로 나누면, 몫은 0, 나머지는 4
>. 앞자리 3×1=3(십진수)로 8진수로 나누면, 몫은 0, 나머지는 3
즉, 34
결과를 더하면 340+70=420 (10진수로 216)
따라서, 8진수 34와 12를 곱한 결과는 420입니다.
4-4) 8진수 나눗셈
8진수_octal 나눗셈은 10진수 나눗셈과 비슷하지만, 결과를 8진수로 유지해야 합니다.
예를 들어, 8진수 752를 4로 나눠보겠습니다.
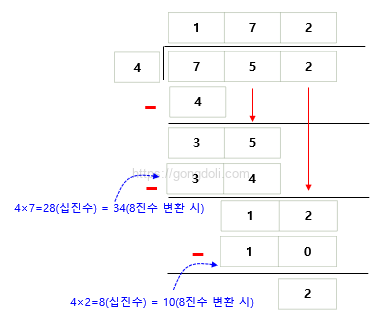
나눗셈 과정을 해보면
7 ÷ 4 = 4이고, 다음 자리 내림하면
35 ÷ 4 = 34 (4×7=28[십진수]이고, 이것을 8진수로 나누면 몫은 3, 나머지는 4 즉, 34가 됩니다. )
12 ÷ 4 = 3 (4×2=8[십진수]이고, 이것을 8진수로 나누면 몫은 1, 나머지는 0 즉, 10가 됩니다. )
따라서, 8진수 752를 4로 나눈 결과는 172, 나머지는 2입니다.