Contents
1. AC 회로의 저항과 리액턴스?
AC 회로의 저항과 리액턴스는 전기 회로에서 중요한 개념입니다.
이를 이해하기 위해서는 전기의 기초적인 원리와 전류의 흐름, 그리고 교류와 직류의 차이를 알아야 합니다.
AC 회로의 저항과 리액턴스 모두 전류의 흐름을 방해하는 것은 동일합니다.
물에 비유해서 설명해보도록 하겠습니다.
저항(Resistance)은 물이 흐르는 파이프를 생각해보겠습니다.
파이프의 내부가 까다로운 장애물로 가득찬 경우, 물이 흐르는 속도가 느려지고 힘이 필요합니다.
이 장애물은 물의 흐름을 제한하는데, 이것이 바로 저항입니다.
전기 회로에서도 저항은 전류의 흐름을 제한하고, 전압에 의해 전류가 흐를 때 열을 발생시킵니다.
리액턴스(Reactance)는 이번에는 물의 운동을 더 생각해겠습니다.
예를 들어, 물이 왕복하는 운동을 생각해보겠습니다.
수면을 위아래로 움직이는 파도와 비슷한 개념입니다.
이때 물의 질량이나 운동량이 파도의 크기와 진폭에 영향을 줍니다.
전기 회로에서 리액턴스는 주파수에 따라 변하는 전기적인 운동이나 반응을 나타냅니다.
이것은 콘덴서와 인덕터에서 발생하며, 전류의 변화를 제어합니다.
즉, AC 회로의 저항은 전류의 흐름을 제한하고 열을 발생시키는데, 이것은 물이 파이프를 통과할 때의 저항과 비슷합니다.
반면에 리액턴스는 전기 회로의 주파수에 따라 전류의 흐름을 제어하는데, 이것은 물의 운동이나 파도의 크기와 비슷합니다.
- 연관 참조 : 저항과 저항률(resistivity), 개념, 차이, 예제 풀이,중요성
- 연관 참조 : 저항기 종류와 장단점, 저항률이란?,저항 vs. 저항률, 종류12가지
- 연관 참조 : 직렬 및 병렬 저항 계산, 직렬 저항 예제, 병렬 저항 예제, 직병렬 저항 예제
- 연관 참조 : 오옴의 법칙 원리, 개념, 예제로 이해하기,전력 구하기,파이 차트
- 연관 참조 : 병렬 저항 계산기, Parallel Resistance Calculator,사용 방법
- 연관 참조 : DC와 AC 차이점, 전기란?,전류란?,진짜 전류의 방향?, DC와 AC전류 더 위험한 건?
2. AC 회로의 저항
직류 전류(DC)는 전기 충전의 흐름이 한 방향으로 흐릅니다.
전압과 전류는 DC에서 일정한 극성과 방향을 유지합니다.
직류의 원천은 배터리입니다. 반면 교류 전류(AC)는 전기 충전의 흐름이 주기적으로 방향을 바꿉니다.
AC에서 전압은 시간이 지남에 따라 양극성과 음극성을 바꿉니다.
이전 구문에서 언급한 것처럼, 이러한 전압의 극성 변화는 전류 방향의 변경으로 인해 발생합니다.
가장 흔한 AC 공급 형태는 사인파입니다.
전류의 수학적 함수는 V(t) = V최대값 sin(ωt)로 설명됩니다.
여기서 V(t)는 시간의 함수이며, t는 초 단위의 변수이고, V최대값은 사인파의 양 및 음의 최대값을 나타냅니다.
ω는 각주파수이며, f는 주파수를 나타냅니다.
직류 회로에서는 전류, 전압 및 전력의 계산이 오옴의 법칙을 사용하여 수행됩니다.
여기서 전압과 전류의 극성이 일정하다고 가정됩니다.
순수 저항성 AC 회로의 경우, 인덕턴스 및 캐패시턴스의 값은 무시됩니다.
따라서 전류, 전압 및 전력의 계산은 오옴의 법칙과 키르호프 회로 법칙의 원리를 따릅니다.
다른 점은 순간적 최대 최소값이나 rms 값의 사용입니다.
2-1) DC와 AC에서의 저항
저항은 수동적인 장치입니다.
그 자체로는 어떤 에너지도 소비하거나 생산하지 않습니다.
전기 에너지는 열의 형태로만 소비됩니다.
DC 전원이 주어진 저항 회로와 AC회로의 저항 회로는
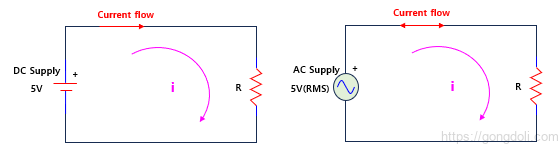
직류 저항 회로에서, 전압 대 전류의 비율인 저항은 선형적입니다.(오옴의 법칙, V=IR)
교류 회로에서, 전압 대 전류의 비율은 주로 공급 주파수 f와 위상 각도 또는 위상 차이 φ에 의존합니다.
따라서 AC 회로의 저항을 나타내는 용어로 임피던스가 사용됩니다.
(임피던스는 저항과 리액턴스 개념을 모두 포함합니다.)
왜냐하면 임피던스는 크기와 위상을 모두 갖고 있기 때문에 DC 회로의 저항과 대조적입니다.
임피던스의 기호는 Z입니다.(Z=V/I)
2-2) V-I 상관 관계
AC와 DC 회로에서의 저항은 동일한 값을 갖습니다.
AC 회로에서도 저항은 전압과 전류 간의 관계를 나타내는데, 이는 오옴의 법칙에 따라서 V=IR로 표현됩니다.
(여기서,V는 전압,I는 전류,R은 저항)
AC 저항 회로에서, 전압과 전류는 시간에 따라 변화합니다.
이때 전압과 전류는 최대값에서 시작하여 최소값까지 변화하게 되는데, 이들은 정확히 동일한 시간에 상승하고 하강하여 “인페이즈(in phase)”라고 합니다.
이는 순수 저항 회로에서의 특징입니다.
예를 들어, AC 회로에서 전류는 I(t)=IMaxsin(ωt)로 표현됩니다.
이것은 사인 함수를 따라 시간에 따라 변화하는 전류를 나타냅니다.
여기서 IMax는 최대 전류 값이고, ω는 각주파수입니다.
전압은 V(t)=VMaxsin(ωt)로 나타낼 수 있습니다.
이것은 최대 전압 값과 각주파수에 따라 변하는 시간에 따른 전압을 의미합니다.
순수 저항 회로에서는 위상 차이가 없으므로, 전압과 전류의 관계는 단순합니다.
전압과 전류는 동일한 시간에 변화하며, 이는 저항의 특성을 나타냅니다.
이러한 관계를 수식적으로는 V(t)= IMaxRsin(ωt)로 표현할 수 있습니다.
여기서 R은 저항의 값입니다.
3. AC 회로의 저항 예제
3-1) 예제 1
AC 저항이 60 Ω인 전기 설비를 240Vrms AC 단상 전원 공급기에 연결하고, 단상 전원 공급기에서 빠져나가는 전류와 전기 설비에서 소비하는 전력을 계산해 보겠습니다. 또한 전류와 전압 사이의 위상 관계를 보여주는 위상 다이어그램도 그려보겠습니다.
3-1-1) 전류 계산
AC 회로에서 전류는 다음과 같이 계산됩니다.
I = Vrms / Z
- 여기서
- Vrms는 단상 전원 공급기의 rms 전압
- Z는 임피던스
주어진 문제에서 임피던스는 AC 저항과 같으므로 Z=R=60Ω 입니다.
I=V/R=240V/60Ω=4A
3-1-2) 전력 계산
전력은 다음과 같이 계산됩니다.
P=Vrms×I×cos(ϕ)
- 여기서 ϕ는 전압과 전류 사이의 위상 각도
- 순수한 저항의 경우, 위상 각도는 0이므로 cos(ϕ)=1
즉, P=240V×4A×1=960 W
3-1-3) 위상 diagram
저항 성분에 위상 차이가 없기 때문에(θ = 0), 해당 위상 다이어그램은 다음과 같습니다.
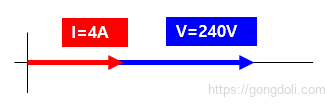
3-2) 예제 2
V(t) = 100 x cos(ω t + 30°)로 정의되는 사인형 전압 공급기는 50Ω의 순수 저항에 연결됩니다.
회로에 흐르는 전류의 임피던스와 피크값을 결정하고 해당하는 위상 다이어그램을 그려 보겠습니다.
3-2-1) Peak값
V(t) = 100 x cos(ω t + 30°) => 주어진 전압 함수에서 피크값은 직접 주어져 있으므로, 피크값은 100V입니다.
3-2-2) 회로 임피던스 계산
순수 저항에 연결된 AC 회로에서 임피던스는 저항과 동일합니다.
따라서 임피던스는 50 Ω입니다.
3-2-3) 위상 다이어그램
저항을 가로지르는 정현파 전압은 순수하게 저항성 회로의 공급 전압과 같습니다.
이 전압을 시간 영역의 식에서 위상 영역의 식으로 변환하면
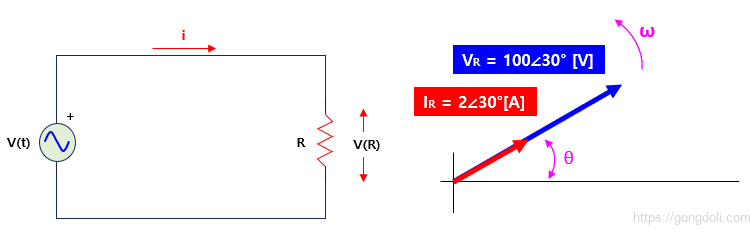
따라서 전압의 피크값은 100V이고, 회로의 임피던스는 50 Ω입니다.
위상 다이어그램에서는 전압과 전류가 “인페이즈“임을 나타냅니다.
4. AC 회로의 저항과 리액턴스의 중요성
AC 회로의 저항과 리액턴스는 제어된 회로 설계에서 매우 중요한 역할을 합니다.
4-1) 저항의 중요성
저항은 전류를 제한하고 전력을 소모합니다.
회로에서의 저항은 전류의 흐름을 제어하고 전압을 안정화시키는 데 도움이 됩니다.
안정된 전류와 전압은 회로의 안정성과 신뢰성을 보장합니다.
특히 고온이나 습도 등의 환경 조건이 변할 때 저항은 회로의 성능을 유지하는 데 중요합니다.
4-2) 리액턴스의 중요성
리액턴스는 콘덴서나 인덕터와 같은 회로 요소의 반응을 나타냅니다.
AC 회로에서는 주파수에 따라 리액턴스가 변화하므로, 회로의 동작도 영향을 받습니다.
리액턴스는 주파수에 따라 전류의 흐름을 제어하고, 회로의 반응을 조절합니다.
따라서 리액턴스를 이해하고 고려하는 것이 중요합니다.
4-3) 상호작용과 회로 설계
AC 회로의 저항과 리액턴스는 상호작용하여 전체 임피던스를 형성합니다.
이는 회로의 효율성과 성능에 영향을 미칩니다.
제어된 회로 설계에서는 저항과 리액턴스를 고려하여 회로를 최적화해야 합니다.
적절한 저항과 리액턴스의 조합은 회로의 안정성을 유지하고 효율성을 향상시킵니다.
따라서 저항과 리액턴스의 중요성을 이해하고 이를 고려하여 제어된 AC 회로를 설계하는 것이 핵심적입니다.
이를 통해 안정성과 효율성을 동시에 확보할 수 있습니다.