PWM 회로 설계,동작원리(구형파,미분기,오차증폭기,삼각파,비교기)

Contents

1. PWM 회로란?
2. PWM 회로 설계의 기본 동작 원리?
3. 구형파 발생회로
- 3-1) 동작 원리
- 3-2) 출력파형 펄스 폭
4. 미분 회로
5. 삼각파 발생 회로
6. 오차 증폭기 회로
7. 비교기

1. PWM 회로란?

전자 회로를 다루다 보면 가장 자주 마주치는 기술이 바로 PWM(Pulse Width Modulation, 펄스폭 변조)입니다.
PWM은 펄스의 폭을 조절해 전력이나 밝기, 속도처럼 연속적인 값을 만들어내는 방식인데, 스위칭 전원이나 모터 제어, 심지어 인버터까지 거의 모든 분야에 쓰입니다.
PWM 회로 설계를 제대로 이해하려면, 단순히 사각파를 만드는 수준이 아니라 기준전압 생성부터 삼각파 발생, 비교기 동작, 오차 증폭기 역할, 그리고 MOSFET 드라이버까지 이어지는 흐름 전체를 하나의 제어 시스템으로 바라봐야 합니다.

연관 참조 : 미분기,회로 수식,RC 미분기 동작 원리,입력 파형에 따른 출력 파형, 예제1
연관 참조 : 인버터 회로 원리,기본 회로 및 동작 원리
연관 참조 : 기본 파형의 종류,사인파, 삼각파, 사각파, 예제1, 각 파형 비교

2. PWM 회로 설계의 기본 동작 원리?

PWM 회로 설계를 제대로 이해하려면 먼저 전체 동작 흐름을 큰 그림에서 볼 필요가 있습니다.
PWM 제어는 단순히 펄스를 만들고 스위치를 켜고 끄는 수준이 아니라, 여러 개의 회로 블록이 서로 신호를 주고받으며 하나의 제어 시스템처럼 움직입니다.

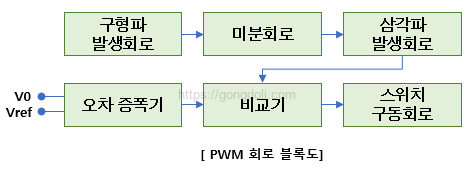
가장 먼저 기준전압(Vref)이 만들어지고, 이 기준을 바탕으로 삼각파나 톱니파 같은 기준 파형이 생성됩니다.
이 파형은 PWM 회로 설계에서 스위칭 타이밍을 결정하는 ‘리듬’ 역할을 합니다. 여기에 DIM 신호나 피드백 전압처럼 외부에서 들어오는 제어전압이 더해지면, 비교기에서 삼각파와 제어전압을 서로 비교해 듀티비가 결정됩니다.

이렇게 생성된 PWM 신호는 오차 증폭기를 거치며 한 번 더 보정되고, 이후 MOSFET 스위칭 회로로 전달되어 실제 부하(램프, LED, 모터, 트랜스 등)를 구동합니다.
최종적으로 부하에서 다시 피드백 신호가 돌아오고, 제어 IC는 이 값을 기준으로 PWM을 자동으로 조절하면서 전체 회로를 안정화합니다.

결국 PWM 회로 설계의 핵심은
기준파형 생성 → 비교 → 듀티 조절 → MOSFET 구동 → 피드백 안정화
이 흐름을 얼마나 정확하게 구성하느냐에 달려 있으며, 이 과정이 PWM 품질을 결정하는 가장 중요한 부분이라고 할 수 있습니다.

3. 구형파 발생회로

PWM 회로 설계를 이해하려면 가장 먼저 구형파(Clock) 신호가 어떻게 만들어지는지 살펴볼 필요가 있습니다.
PWM의 기준이 되는 삼각파·톱니파는 모두 이 Clock 신호를 기반으로 생성되기 때문에, 구형파 발생 회로는 PWM 회로 설계에서 ‘출발점’이라고 할 수 있습니다.

여기에서는 위에 그림과 같이 74AC04 인버터 두 개를 이용한 비안정 멀티바이브레이터(oscillator) 형태로 예를 들어 설명하겠습니다.

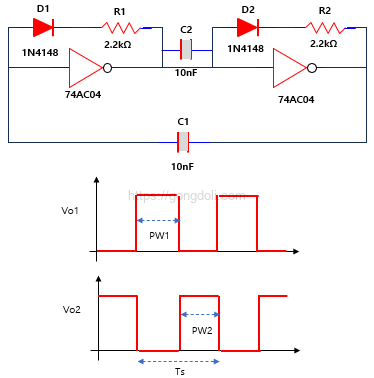
74AC04는 고속 CMOS 인버터 IC로, 이 인버터 2개와 RC 네트워크(R1, R2, C1, C2)를 이용하면 단순하면서도 안정적인 비안정 발진기(oscillator) 를 만들 수 있습니다.
이 회로는 별도의 삼각파 발생기와 결합되어 PWM 회로 설계의 기준 주파수를 만들어 주며, 특히 소형 SMPS, LED Driver, 각종 인버터 회로에서 널리 사용되는 방식입니다.

3-1) 동작 원리

인버터(74AC04)는 입력 신호가 High이면 출력이 Low가 되고, 입력이 Low이면 출력은 High가 됩니다.
이 출력이 RC 네트워크를 통해 다시 인버터 입력으로 전달되면서 충전·방전 지연(Delay)이 발생합니다.
이 지연 때문에 인버터 입력은 일정 시간 High로 유지되다가 다시 Low로 바뀌고,
두 번째 인버터를 거치면서 위상이 반전된 다음 다시 첫 번째 인버터 입력으로 돌아오며
결국 신호가 계속 High ↔ Low 사이에서 oscillation(진동) 하게 됩니다.

이 과정을 반복하면서 일정한 주기의 구형파가 만들어지고, 이 신호가 PWM 회로 설계의 기준 Clock 역할을 하게 됩니다.

3-2) 출력파형 펄스 폭

33 kHz 주파수를 만들기 위한 R, C 값을 선정해 보겠습니다.

비안정 멀티바이브레이터는 양쪽에서 번갈아 충·방전되기 때문에 주기(Ts)는 다음과 같습니다.

Ts = 1/(PW₁+PW₂) = 2×0.693×R×C

따라서 주파수 f는,

f = 1/Ts = 1/(2×0.693×R×C)

즉, f = 1/(1.386×R×C)

이 식을 기준으로 PWM 회로 설계에서 원하는 주파수(33 kHz)를 만들기 위해 R과 C 값을 결정합니다.

주파수 33KHz를 만들기 위해서는

f=33000 Hz

따라서 필요한 RC 값은

R×C = 1/(1.386×33000)

계산하면

R×C = 2.17×10⁻⁵

즉, R×C≈21.7 μs

R, C 값 선택 방법은 어떤 조합이든 RC = 21.7 µs이면 됩니다.

먼저 C를 선택

노이즈 영향 감소
주파수 안정성 확보
너무 작은 C는 발진 불안정
너무 큰 C는 IC 충·방전 전류가 커져 발진 불안정

실제 대략 1 nF ~ 10 nF 범위가 가장 적절합니다.

예를 들어 C = 4.7 nF를 선택하면,

R=21.7μs/4.7nF

R≈4.6 kΩ → 즉 4.7 kΩ 사용하면 됩니다.

이것을 다시 표로 정리해보면

C 값	계산된 R	실제 사용 R값	실제 주파
4.7nF	4.6kΩ	4.7kΩ	약 32.4 kHz
5.6nF	3.9kΩ	3.9kΩ	약 32.7 kHz
3.3nF	6.6kΩ	6.8kΩ	약 31.7 kHz
10nF	2.2kΩ	2.2kΩ	약 33.0 kHz

위 조합 중 C = 10 nF, R = 2.2 kΩ 조합이 가장 이상적으로 33 kHz에 근접합니다.

펄스폭이 동일하다는 것은 듀티비를 50% 근처로 유지하는 설계를 의미합니다.
(비안정 멀티바이브레이터는 R1 = R2로 맞추면 거의 50%)

따라서,

R1 = R2 = 2.2 kΩ
C1 = C2 = 10 nF

이 조합이 33 kHz, 50% 듀티비, 회로 안정성 모두 만족하는 선택이라고 할 수 있습니다.

4. 미분 회로

구형파 발생 회로에서 만든 신호는 그대로 사용하기보다는, PWM 회로 설계 과정에서 시간 축에서의 변화를 더 선명하게 잡아내기 위한 ‘미분 회로’를 거치는 경우가 많습니다.
특히, 스위칭 타이밍을 정밀하게 제어하거나, 임펄스 신호를 만들어 게이트 드라이브 또는 보호회로에 사용해야 할 때 매우 유용합니다.

미분 회로는 고역 통과 필터(High-Pass Filter) 구조를 사용합니다.
보통은 직렬 커패시터(C)와 병렬 저항(R) 으로 구성되며, 입력으로 구형파가 들어오면 출력은 순간적으로 튀는 날카로운 임펄스(Spike) 형태가 됩니다.

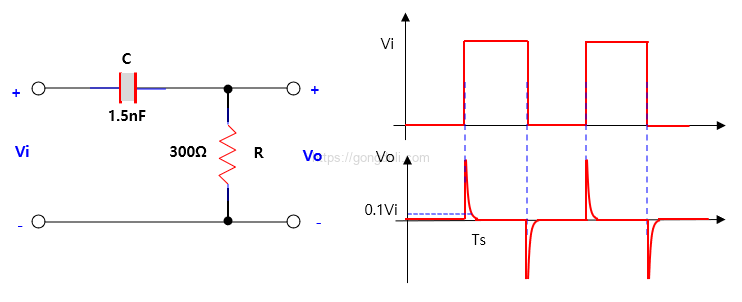
구형파의 상승 에지 → 양의 임펄스
구형파의 하강 에지 → 음의 임펄스

임펄스는 순간적으로 크게 나오지만, 저항 R을 거치며 지수 함수 형태로 서서히 감쇄합니다.

출력 전압의 감쇄 특성은

V(t) = V₀e^−t/RC

여기서 우리가 구하고 싶은 것은, 초기값의 10%까지 떨어지는 데 걸리는 시간(ts) 입니다.

따라서, 0.1V₀ = V₀e−^ts/RC

정리하면, ts = −RCln(0.1)

즉, ts = 2.3026×RC

R = 300Ω, C = 1.5nF으로 정했다고 가정하면

RC 값은 RC = 300×1.5×10⁻⁹ = 450×10⁻⁹=450ns

ts 값은 ts = 2.3026×450ns ≈ 1036ns ≈ 1.04μs

즉, 이 미분 회로는 약 1 μs 정도의 폭을 가진 임펄스 파형을 만들어 출력합니다.
PWM 회로 설계에서 이 정도의 임펄스 폭은 스위칭 타이밍 검출이나 트리거 신호로 쓰기에 적당한 수준입니다.

고역 통과 필터 계산기 바로가기

PWM 회로 설계에서 미분 회로를 사용하는 이유는

구형파의 상승·하강 에지를 강조하여 타이밍 신호로 사용
PWM 스위칭 지연 보정(Delay Compensation)
데드타임 생성
보호회로(OLP / OCP 등)에서 급격한 변화 감지
MOSFET 드라이버 입력 신호 정리(Spike Detection)

즉, 미분 회로는 단순한 필터가 아니라, 구형파의 에지 정보를 추출해 PWM 제어의 정밀도를 올리는 핵심 보조 회로입니다.

5. 삼각파 발생 회로

구형파를 미분해 좁은 펄스(에지 임펄스)를 만들고, 그 펄스를 74AC04 인버터/트랜지스터 입력을 통해 정류·클램핑시켜 최종적으로 RC(18k–5.6nF)에서 원하는 펄스 형태로 얻는 구조입니다.

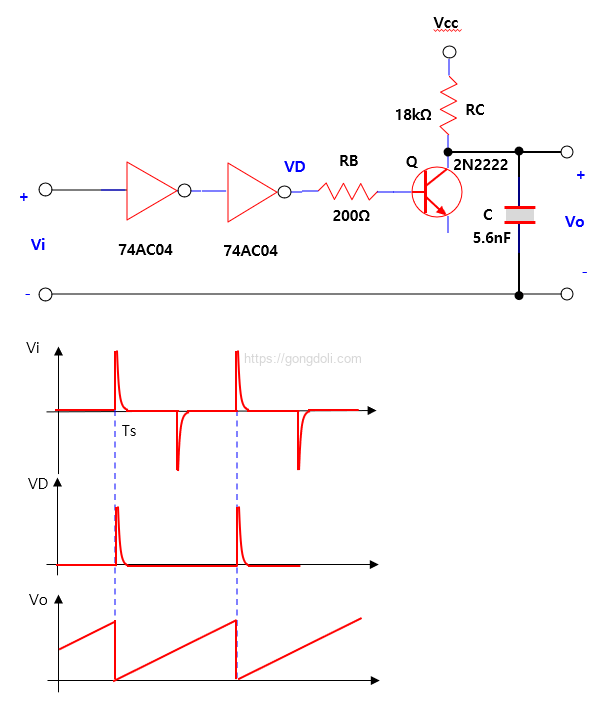
위에 회로에서 미분 출력(아날로그 스파이크)은 74AC04의 입력으로 들어갑니다.
74AC04는 CMOS 인버터로서 입력단의 내부 구조(입력 보호/정류 소자, 게이트 임피던스 등) 때문에 매우 짧고 낮은 에너지의 아날로그 스파이크는 다음 중 하나로 처리됩니다.

스파이크가 입력 스레시홀드(≈ Vcc/2 수준)보다 작으면 논리 출력이 토글되지 않고 입력에서 내부 클램핑(또는 누설)됩니다.
스파이크가 충분히 크면 인버터가 전환하며 다음 단계(베이스)로 논리 펄스를 보내게 됩니다.

따라서 미분 임펄스의 진폭/폭이 74AC04의 입력 전압 임계값과 비교해 충분해야 디지털 전환이 안정적으로 일어납니다.
이 점은 PWM 회로 설계에서 매우 중요합니다.

74AC04 출력이 BJT 베이스 저항(200 Ω)을 통해 베이스에 전압을 준다면, 베이스-이미터 접합은 정류(클램프) 역할을 합니다.
베이스에 들어오는 전압이 V_BE ≈ 0.6–0.8 V를 초과하면 BJT가 도통(ON)하여 컬렉터를 풀업(R_C) 쪽에서 접지 쪽으로 끌어당깁니다.

즉, 미분으로 생긴 좁은 양(positive) 펄스만이 베이스-이미터 다이오드에 의해 전달되어 트랜지스터를 순간적으로 켭니다.
음의 펄스는 B-E 접합으로는 반대 방향 바이어스되어 차단됩니다(정류 효과).

이 때문에 “구형파 → 미분 → 74AC04 → BJT 베이스” 경로는 사실상 양 에지에서만 활성화되는 정류+클램프 방식의 펄스 생성기가 됩니다.

트랜지스터가 턴온되면 컬렉터 전압은 거의 GND(포화 약 0.1–0.3V)로 낮아집니다.
컬렉터에 연결된 18k 풀업과 5.6 nF 커패시터는

트랜지스터가 ON일 때 컬렉터는 순간적으로 내려가며 Cout은 방전 또는 (정확한 극성에 따라) 충전됩니다.
BJT가 OFF되면 R_C가 Cout을 VCC 쪽으로 천천히 다시 끌어올립니다.
시정수 τ_out = R_C · C_out = 18kΩ × 5.6 nF ≈ 100.8 μs.
따라서 출력 펄스의 하강은 매우 빠르지만, 상승(회복)은 수십–수백 마이크로초로 길게 유지됩니다.
이로 인해 실제 출력 파형은 “짧은 펄스가 컬렉터를 순간적으로 풀다운 → 느리게 복구되는 형태”가 됩니다.

정리하면, 이 회로는 미분으로 생긴 아주 짧은 에지 펄스를 74AC04와 BJT의 베이스-이미터 다이오드에 의해 정류·증폭하고, 그 결과를 큰 τ를 가지는 RC에서 천천히 회복되는 펄스로 변환하는 구조입니다.
이 방식은 “짧은 에지 트리거 → 출력에서 시간적 통합”을 의도한 설계로, PWM 회로 설계에서 펄스 폭, 타이밍, 평균값 제어에 유용하지만, 반대로 펄스가 너무 짧아 디지털 인식이 안 되거나 입력이 클램핑되어 전환이 불안정할 위험도 있습니다.

6. 오차 증폭기 회로

PWM 회로 설계를 이해하기 위해서는 출력 전압이 어떻게 안정되는지, 즉 오차 증폭기가 어떻게 동작하는지를 정확히 알 필요가 있습니다.
오차 증폭기 회로는 사용자 부하에 연결된 출력 전압을 감지하여, 그 값이 기준전압(Vref)과 얼마나 차이나는지를 실시간으로 비교하고 PWM 듀티에 반영하는 과정입니다.

아래 회로구조는 전형적인 비반전 기준 기반의 오차 증폭기 구조이며, PWM 회로 설계에서 가장 널리 사용되는 피드백 형태입니다.

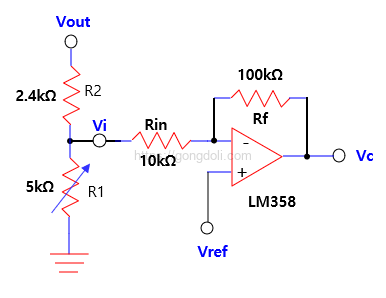
출력단에는 직접 높은 전압이 걸리기 때문에 이를 그대로 연산증폭기에 넣을 수는 없습니다.
그래서 R2(2.4kΩ)와 R1(5kΩ 가변저항)으로 구성된 분압 회로에서 전압을 적절히 낮추어 Sensing합니다.

여기서 Vi는 출력전압의 “분배된 값”이며, R1은 미세한 출력전압 변화나 목표값을 맞추기 위해 조정용으로 사용됩니다.
PWM 회로 설계에서 이 가변저항은 보통 레귤레이션 정밀 조정, 즉 원하는 출력 레벨을 잡는 역할을 합니다.

분배 전압값

Vi=Vout×(R1/R1+R2)

즉, R1을 조절하면 Vi도 변하므로, 결과적으로 PWM 회로 설계에서 목표 전압을 쉽게 세팅할 수 있습니다.

이 분압된 Vi는 Rin(10kΩ)을 통해 오차 증폭기 LM358의 ( – )입력으로 들어갑니다.
여기서 Rin은 입력 단계의 안정성과 노이즈 제거 역할을 합니다.

PWM 회로 설계에서 이 Rin + Rf 조합은 최종적으로 오차 증폭기의 이득(Gain)을 결정하는 매우 중요한 부분입니다.

LM358의 출력 Vc는 곧바로 PWM 생성 회로의 기준전압 역할을 하거나 비교기 입력으로 들어가 듀티를 결정하는 데 사용됩니다.
이때 Rf(100kΩ)이 (–) 입력으로 다시 귀환되어 오차 증폭기의 전체 이득을 설정합니다.

오차증폭기의 폐루프 이득은

A = 1+(Rf/Rin) = 1+(100kΩ/10kΩ) = 11

출력전압 변화가 작더라도 LM358의 출력은 11배 정도 증폭되므로 PWM 듀티가 빠르고 정확하게 보정됩니다.
PWM 회로 설계에서 이 피드백저항 Rf는 전체 시스템 안정성에 영향을 주기 때문에 매우 중요한 요소입니다.

7. 비교기

오차 증폭기에서 생성된 Vc는 바로 다음 단계인 비교기로 전달됩니다.
여기서부터 PWM 파형이 실제로 만들어지는 핵심 구간입니다.

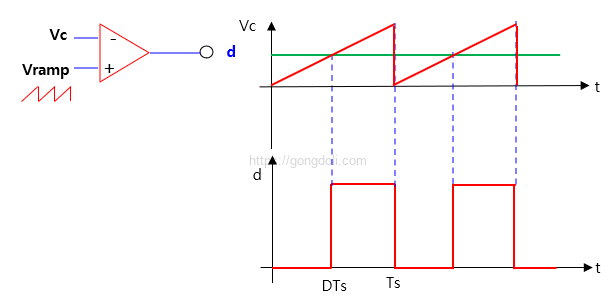
① 삼각파 > Vc

d 출력 = High
→ 펄스가 ON
→ 듀티 증가

② 삼각파 < Vc

d 출력 = Low
→ 펄스가 OFF
→ 듀티 감소

이 비교를 삼각파 주기마다 반복하면서 최종적으로 펄스폭이 자동으로 조절되는 PWM 신호가 형성됩니다.