Contents
1. 개요
필터는 신호를 걸러내는 회로로, 필요한 신호만을 통과시키고 원하지 않는 신호를 차단합니다.
이러한 필터는 일반적으로 수동 부품 또는 능동 부품을 사용하여 설계됩니다.
수동 부품은 저항기, 인덕터 및 캐패시터로 구성됩니다. 반면, 능동 부품은 트랜지스터, FET 및 오프앰프 등이 포함됩니다.
필터에는 저역 통과 필터(LPF), 고역 통과 필터(HPF), 대역 통과 필터(BPF) 등이 있습니다.
여기서는 먼저, 수동 저역 통과 필터에 대해 알아보겠습니다.
수동(혹은 능동) 저역 통과 필터는 주파수가 낮은 신호만을 통과시키고 고주파 신호를 감쇄하거나 차단합니다.
이 필터는 주파수 0Hz부터 차단 주파수 ‘fc’까지의 신호만을 허용합니다.
차단 주파수 값은 회로에 사용된 부품 값에 따라 달라집니다.
수동 저역 통과 필터는 구성에 따라 다양한 종류가 있습니다.
RC 수동 저역 통과 필터, RL 수동 저역 통과 필터, RLC 수동 저역 통과 필터 등이 있습니다.
이러한 수동 저역 통과 필터는 회로 구성 및 요구되는 필터링 특성에 따라 선택됩니다.
- 연관 참조 : 용량성 리액턴스, 원리, 예제 3개, 그래프
- 연관 참조 : RL 수동 저역 통과 필터, LPF 종류,동작 원리,상한 차단 주파수, 예제1
- 연관 참조 : 수동 RC 고역 통과 필터,Ideal,Real,주파수 응답,출력 전압 및 게인,예제1, 2차필터
- 연관 참조 : 수동 대역 통과 필터란?, RLC을 사용한 BPF회로,주파수 응답, 예제1,요약
- 연관 참조 : 능동 저역 통과 필터,1차 LPF, 전압 이득, 예제1
2. 수동 저역 통과 필터란?
간단한 RC 수동 저역 통과 필터(LPF)는 전기 회로에서 주파수를 분리하는 역할을 합니다.
이 필터는 저항과 캐패시터를 사용하여 구성되어 있으며, 이 두 요소가 직렬로 연결됩니다.
이 필터의 주요 목적은 주파수가 일정 값 이하인 신호를 통과시키고, 그 이상인 신호를 차단하는 것입니다.
이러한 필터를 “1차 필터”로 부르는 이유는 회로에 반응성 요소가 하나만 있기 때문입니다.
이 경우에는 캐패시터가 그 역할을 하며, 이를 통해 주파수를 분리하고 제어합니다.
다른 방식으로 말하면, 이 필터는 회로에서 반응성 구성 요소가 하나만 있는 단순한 필터입니다.
반면에 고차 필터는 두 개 이상의 반응성 구성 요소가 있습니다(예: 캐패시터와 인덕터의 조합).
필터 설계에서 “차수”라는 용어는 회로에 있는 반응성 구성 요소의 수를 나타내며, 이는 필터의 차단 주파수 이상에서의 감쇠 속도를 결정합니다.
1차 RC LPF의 경우, 감쇠 속도는 주파수가 차단 주파수를 초과할 때 20 dB/분(또는 6 dB/옥타브)로 감소합니다.
1차 RC 수동 저역 통과 필터의 동작 방식은 다음과 같습니다.
낮은 주파수에서는 캐패시터의 반응성이 높아져 입력 신호의 대부분이 저항에 나타납니다.
이로 인해 출력 신호의 크기가 작아지게 됩니다.
그러나 주파수가 증가함에 따라 캐패시터의 반응성이 감소하게 되고, 이에 따라 출력 신호의 크기도 증가합니다.
이를 통해 필터는 주파수가 일정 값 이상인 신호를 차단하고 낮은 주파수 신호만을 통과시킵니다.
또한 AC 회로에서 커패시터의 용량 리액턴스는 다음과 같이 주어진다는 것을 알고 있습니다
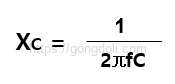
AC 회로의 전류 흐름에 대한 반대를 임피던스, 기호 Z라고 하며, 단일 커패시터로 직렬로 구성된 단일 저항으로 구성된 직렬 회로의 경우 회로 임피던스는 다음과 같이 계산됩니다
3. 수동 저역 통과 필터 출력 전압 계산
임피던스를 대체함으로써 임의의 주파수에 대한 RC 수동 저역 통과 필터의 출력 전압을 계산할 수 있습니다.
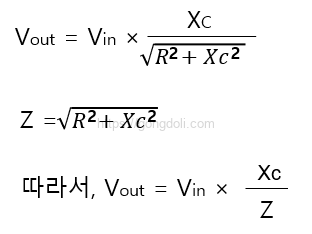
- 여기서
- Vout는 출력 전압입니다.
- Vin는 입력 전압입니다.
- XC는 캐패시터의 용량성 리액턴스입니다.
- R 는 저항의 값입니다.
이 수식은 전압 분배 법칙에 기반하여 캐패시터의 용량성 리액턴스와 저항의 비율을 사용하여 출력 전압을 계산합니다.
4. 수동 저역 통과 필터 예제 풀이
저항과 커패시터 값을 고려하여 출력 전압 값과 커패시터 리액턴스 값을 구해보도록 하겠습니다.
저항 R의 값이 4.7 KΩ이고 커패시터 값이 47 nF라고 하고, 공급되는 입력 교류 전압은 10 V이다.
여기서 우리가 계산할 주파수 값은 1 kHz와 10 kHz입니다.
먼저, 용량성 리액턴스 (XC)를 다음과 같은 공식을 사용하여 계산합니다
XC = 1/ 2πfC
주어진 값
- 캐패시턴스 (C) = 47 nF1000
- 저항(R) = 4.7KΩ
- 입력 전압(Vin) = 10V
- 주파수 (f1) = 1 kHz
- 주파수 (f2) = 10 kHz
값을 대입하면
f1=1kHz의 경우,
XC1 = 1/ (2πfC) = 1/(2π×1×103×47×10−9) = 3386.27Ω
출력 전압은
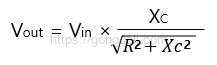
= 10×3386.27/√(47002+3386.272 )= 5.84V
f1=10kHz의 경우,
XC2 = 1/ (2πfC) = 1/(2π×10×103×47×10−9) = 338.62Ω
출력 전압을 구해보면
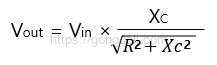
=10×338.62/√(47002+338.622 )= 0.7186V
주파수가 증가함에 따라 용량성 리액턴스의 감소와 출력 전압의 감소는 전형적인 특성입니다.
이러한 변화는 RC 수동 저역 통과 필터의 동작 원리와 밀접한 관련이 있습니다.
첫째로, 주파수가 증가하면 용량성 리액턴스가 감소합니다.
용량성 리액턴스는 주파수에 반비례하기 때문에 고주파에서는 더 낮은 값을 갖게 됩니다.
이것은 캐패시터가 고주파 신호를 통과하기 쉽게 만들어줍니다.
둘째로, 출력 전압도 주파수와 함께 감소합니다.
이는 주로 용량성 리액턴스가 증가함에 따라 발생합니다.
용량성 리액턴스가 증가하면 캐패시터가 전압을 더 많이 “차단”하고, 결과적으로 출력 전압이 줄어듭니다.
위에 예제를 보듯이, 1 kHz와 10 kHz에서의 용량성 리액턴스는 각각 3386.27 Ω에서 338.62 Ω으로 줄어듭니다.
이에 따라 출력 전압은 5.84 V에서 0.718 V로 줄어듭니다.
이러한 결과는 주파수가 증가함에 따라 RC 수동 저역 통과 필터의 동작이 변화함을 보여줍니다.
5. 주파수 응답
5-1) 주파수 응답
수동 저역 통과 필터(LPFF)의 주파수 응답은 다른 주파수의 신호를 어떻게 감쇠하거나 통과시키는지를 설명합니다.
RC 수동 저역 통과 필터의 경우, 주파수 응답은 저주파 신호를 통과시키면서 고주파 신호를 감쇠시키는 능력으로 특징 지어집니다.
저주파에서는 캐패시터의 용량성 리액턴스 (XC)가 저항 (R)에 비해 높기 때문에 대부분의 입력 신호가 거의 영향을 받지 않고 필터를 통과합니다.
주파수가 증가함에 따라 캐패시터의 용량성 리액턴스가 감소하여 입력 신호의 고주파 성분을 더 많이 감쇠시킵니다.
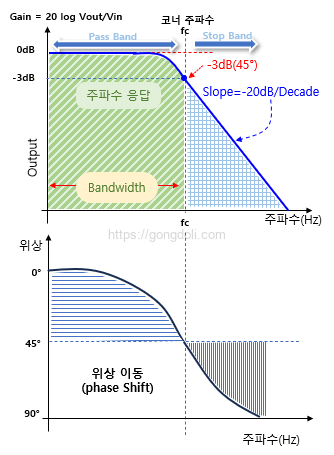
보데 플롯은 필터의 주파수 응답을 보여줍니다.
낮은 주파수에서 거의 평평하게 유지되며 입력 신호의 거의 전체가 출력으로 전달되어 거의 1인 Gain을 갖게 됩니다.
이 상태는 Cut-off 주파수점(ƒc)에 도달할 때까지 유지됩니다.
캐패시터의 리액턴스가 낮은 주파수에서 높기 때문에 캐패시터를 통한 전류 흐름이 차단됩니다.
Cut-off 주파수점 이후에는 회로 응답이 -20dB/ Decade 또는 (-6dB/Octave)의 기울기로 0까지 감소합니다.
이러한 -20dB/ Decade roll-off의 각도는 어떤 RC 조합에서도 항상 동일합니다.
저항된 고주파 신호가 적용되면 Cut-off 주파수점 이후에 크게 감쇠됩니다.
매우 높은 주파수에서 캐패시터의 리액턴스가 매우 낮아지기 때문에 출력 단자에서 단락 조건의 효과를 줍니다.
올바른 저항-캐패시터 조합을 선택하면 특정 값 아래의 주파수가 회로를 통과하는 동안 Cut-off 지점 이상의 주파수가 크게 감쇠되어 회로를 통과할 수 있게 됩니다.
이를 “Low Pass Filter”라고 합니다.
이 유형의 “Low Pass Filter” 회로의 경우, Cut-off, ƒc 포인트 이하의 모든 주파수는 거의 또는 전혀 감쇠되지 않은 상태로 유지되며, 필터의 패스 밴드 영역에 속합니다.
이 패스 밴드 영역은 필터의 대역폭을 나타냅니다.
이 지점 Cut-off 이상의 모든 신호 주파수는 일반적으로 필터의 Stop Band 영역에 속하며, 강하게 감쇠됩니다.
이 “Cut-off”, “corner” 또는 “Breakpoint” 주파수는 캐패시터 리액턴스와 저항이 동일한 주파수 점인 R = Xc = 4k7Ω일 때 발생합니다.
이 상황에서 출력 신호는 입력 신호 값의 70.7%로 감쇄되거나 입력의 -3dB입니다.
R = Xc이지만 출력은 입력 신호의 반만큼이 아닙니다.
이는 두 값의 벡터 합계가 동일하고 따라서 입력의 0.707임을 의미합니다.
회로에 캐패시터가 포함되어 있기 때문에 출력 신호의 위상은 입력 신호의 뒤를 따르게 됩니다.
-3dB 차단 주파수(ƒc)에서 출력 신호의 위상은 -45°입니다.
이는 입력 전압이 변경될 때 캐패시터 판을 충전하는 데 걸리는 시간 때문에 출력 전압(캐패시터 전압)이 입력 신호의 전압보다 “뒤쳐지는” 것입니다.
입력 주파수가 높아질수록 캐패시터의 지연이 더 커지고 회로는 점점 “위상 차이”가 커집니다.
Cut-off 주파수점 및 위상 이동 각도는 다음과 같은 방정식을 사용하여 찾을 수 있습니다:
5-2) 차단 주파수와 위상 이동
차단 주파수와 위상 이동은 다음과 같은 방정식을 사용하여 계산됩니다.
차단 주파수 (ƒc)는 다음과 같이 정의됩니다.
ƒc = 1/ (2πRC)
- 여기서,
- R은 저항 값이고
- C는 캐패시터 값입니다.
위상 이동 (ø)은 다음과 같이 계산됩니다.
위상이동(ø) = −tan−1(2πfRC)
- 여기서,
- f는 주파수 (Hz)이고
- R은 저항 값이고
- C는 캐패시터 값입니다.
이러한 방정식을 사용하여 차단 주파수와 위상 이동을 계산할 수 있습니다.
이것들은 필터의 동작을 이해하고 설계하는 데 중요한 요소입니다.
6. 2차 저역 통과 필터
2차 저역 통과 필터(Second-order Low Pass Filter)는 차단 주파수(ƒc)보다 높은 주파수의 신호를 약화시키면서 낮은 주파수 신호가 최소한의 약화로 통과하는 필터 회로입니다.
1차 필터와 달리 이차 필터는 하나의 반응성 구성 요소(예: 캐패시터)뿐만 아니라 일반적으로 두 개의 캐패시터나 두 개의 인덕터와 함께 사용되는 두 개의 반응성 구성 요소를 포함합니다.
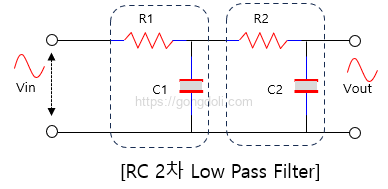
2차 저역 통과 필터의 기본 구조에는 두 개의 반응성 구성 요소와 하나의 저항이 서로 다른 구성으로 배열되어 있습니다.
예를 들어, Sallen-Key 토폴로지, 다중 피드백(MFB) 토폴로지 또는 상태 변수(State-variable) 토폴로지가 있습니다.
각 구성은 이차 필터의 주파수 응답 및 감쇠 특성을 결정하는 피드백 루프를 형성합니다.
Sallen-Key 토폴로지의 경우 두 개의 저항과 두 개의 캐패시터가 피드백 루프를 형성하여 필터의 주파수 응답 및 감쇠 특성을 결정합니다.
MFB 토폴로지는 다중 피드백 경로를 활용하여 원하는 필터 특성을 달성하는 반면, 상태 변수 토폴로지는 다중 오프앰프와 반응성 구성 요소를 사용하여 다양한 필터 설계를 구현합니다.
2차 저역 통과 필터는 1차 필터보다 가파른 roll-off 속도를 나타내어 차단 주파수 이상의 주파수에서 더 나은 신호 약화를 제공합니다.
roll-off 속도는 필터의 이득이 차단(cut-off) 주파수 이상의 주파수에서 증가하는 속도를 나타냅니다.
일반적으로, 이차 필터는 -40 dB/decade 또는 -12 dB/octave의 roll-off 속도를 나타냅니다.
2차 저역 통과 필터의 설계에는 원하는 차단 주파수, 이득 및 롤오프 특성을 달성하기 위해 적절한 구성 요소 값을 선택하는 것이 포함됩니다.
버터워스(Butterworth), 체비셰프(Chebyshev) 및 베셀(Bessel) 디자인과 같은 고급 필터 설계 기술은 패스밴드 평평성, 스톱밴드 감쇠 및 순간 응답 사이의 다양한 균형을 제공합니다.
전반적으로, 2차 저역 통과 필터는 정확한 주파수 제어와 신호 약화가 필요한 오디오 처리, 통신 및 계측과 같은 다양한 전자 응용 분야에서 널리 사용됩니다.
7. 수동 저역 통과 필터의 fc와 2차 필터의 fc
7-1) 수동 저역 통과 필터의 fc
수동 저역 통과 필터의 차단 주파수(ƒc)에서의 이득은 일반적으로 이 중요한 주파수 지점에서의 신호 감쇠 또는 증폭량을 결정하기 위해 계산됩니다.
수동 저역 통과 필터에서 차단 주파수에서의 이득은 일반적으로 이 주파수에서의 출력 전압(Vout)과 입력 전압(Vin)의 비율로 정의됩니다.
수학적으로, 차단 주파수(ƒc)에서의 이득(G)은 다음과 같이 표현될 수 있습니다
G=20×log 10 (Vout / Vin)
여기서
- Vout은 필터의 출력 전압입니다.
- Vin은 필터에 적용된 입력 전압입니다.
- 이득은 종종 두 값을 비교하는 로그 스케일인 데시벨(dB)로 표현됩니다.
차단 주파수(ƒc)에서 출력 전압은 일반적으로 감쇠되어, 입력 전압에 비해 줄어듭니다.
따라서 ƒc에서의 이득은 음수일 것이며, 전압 진폭의 감소를 나타냅니다.
ƒc에서의 구체적인 이득 값은 필터의 설계 매개변수에 따라 달라지며, 저항기 및 캐패시터 값과 필터의 토폴로지와 같은 요소에 의해 결정됩니다.
서로 다른 필터 구성은 ƒc에서의 이득 특성이 다를 수 있습니다.
7-2) 2차 필터의 차단(코너) 주파수
2차 필터에서의 코너 주파수(또는 차단 주파수)는 필터의 반응이 첫 번째 주파수 규칙에서 두 번째 주파수 규칙으로 전환되는 지점을 가리킵니다.
이는 필터의 전체 동작을 결정하는 중요한 매개변수 중 하나입니다.
수학적으로, 2차 필터의 코너 주파수(ƒc)는 다음과 같이 표현됩니다:
fc = 1 / 2π√(R1⋅R2⋅C1⋅C2)
여기서
- R1 및 R2는 필터의 저항 값입니다.
- C1 및 C2는 필터의 캐패시터 값입니다.
코너 주파수는 필터의 저항과 캐패시터 값에 의해 결정되며, 이러한 값들의 조합에 따라 다양한 코너 주파수를 얻을 수 있습니다.
또한, 2차 필터의 코너 주파수는 필터의 전체 응답 특성을 결정하는 데 중요한 역할을 합니다.
7-3) 2차 필터의 주파수 응답
2차 저역 통과 필터의 주파수 응답은 해당 필터가 어떻게 다양한 주파수에 대응하는지를 나타냅니다.
이것은 필터의 동작을 이해하고 설계하는 데 중요한 개념입니다.
2차 저역 통과 필터의 주파수 응답은 일반적으로 주파수에 따른 전압 이득의 그래프로 나타냅니다.
주파수가 낮은 경우 입력 신호의 대부분이 출력으로 전달되며, 이는 전압 이득이 거의 1에 가깝다는 것을 의미합니다.
그러나 주파수가 증가함에 따라 필터는 점차적으로 신호를 감쇠시키며, 출력 신호의 크기가 줄어들게 됩니다.
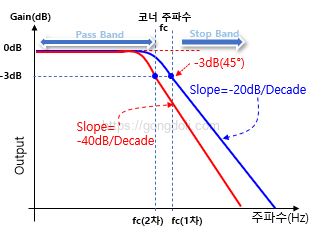
2차 저역 통과 필터의 주파수 응답은 코너 주파수 및 품질 요인(Q-factor)에 따라 결정됩니다.
코너 주파수는 필터의 주파수 응답이 3dB 저하되는 지점을 가리키며, 품질 요인은 코너 주파수 주변에서 필터의 반응 폭과 날카로움을 결정합니다.
일반적으로 2차 저역 통과 필터의 주파수 응답은 코너 주파수를 중심으로 벨 모양의 곡선을 형성하며, 이는 코너 주파수 주변에서 신호 감쇠가 점차적으로 발생함을 나타냅니다.
특히, 코너 주파수 이하에서는 전압 이득이 높고, 코너 주파수 이상에서는 감쇠되는 특성을 보입니다.
이러한 주파수 응답은 필터가 주파수를 어떻게 통과시키고 차단하는지를 잘 이해할 수 있도록 도와줍니다.