Contents
1. RC 회로란 무엇인가?
RC 회로는 ‘저항(Resistor)’과 ‘커패시터(Capacitor)’의 머리글자를 따서 이름이 붙여진 회로입니다.
이 두 가지 부품은 전자 회로에서 각각 중요한 역할을 담당하는데, RC 회로에서는 저항과 커패시터가 상호작용하며 매우 흥미로운 전기적 특성을 만들어냅니다.
특히, RC 회로 충전 시간이 어떻게 결정되는지가 매우 중요한 포인트입니다.
이를 알면 우리가 사용하는 다양한 전자 기기의 동작 원리를 쉽게 이해할 수 있습니다.
1-1) 저항과 커패시터의 역할 설명
먼저, 저항(Resistor)에 대해 살펴보겠습니다.
저항은 전류의 흐름을 방해하는 역할을 합니다.
물을 흘려보낼 때 좁은 파이프를 생각하면 쉬운데, 파이프가 좁으면 물의 흐름이 느려지듯, 저항이 높으면 전류의 흐름이 느려집니다.
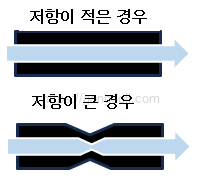
어떤 분이 “저항이 높으면 전기세를 덜 내나요?”라고 질문한 적이 있었습니다.
답변은 “아니요”입니다.
저항은 단순히 전류의 양을 제한할 뿐, 전기세와는 별개입니다.
하지만 이 질문은 저항의 역할을 이해하는 데 좋은 예가 됩니다.
저항은 전류의 흐름을 적절히 조절하는 ‘수문’ 같은 역할을 합니다
이제 커패시터(Capacitor)를 보겠습니다.
커패시터는 전하(Charge)를 저장하는 역할을 합니다.
물통에 물을 저장하는 것과 비슷하다고 생각하면 됩니다.
커패시터가 전류를 받으면 그 안에 전하가 저장되고, 다 차면 더 이상 전류를 받을 수 없습니다.
이 과정을 ‘충전’이라고 하는데, 이 충전이 바로 RC 회로에서 중요한 개념입니다.
즉, RC 회로 충전 시간은 커패시터가 얼마나 빨리 충전되는지를 결정하는 중요한 요소입니다.
1-2) RC 회로의 기본 구조
RC 회로의 구조는 매우 간단합니다.
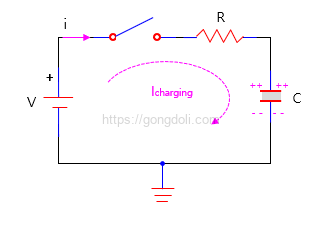
저항과 커패시터가 직렬로 연결된 형태인데, 이 회로를 통해 전원이 인가되면 전류가 흐르며 커패시터가 충전되기 시작합니다.
처음에는 빠르게 충전되다가 점점 속도가 느려지며, 결국엔 충전이 끝나게 됩니다.
이때 중요한 것이 바로 RC 회로 충전 시간입니다.
RC 회로 충전 시간은 커패시터가 63.2% 정도 충전되는 데 걸리는 시간을 말하는데, 이 시간은 저항값과 커패시터의 용량에 의해 결정됩니다.
이를 타임 컨스턴트(Time Constant)라고도 부릅니다.
만약 저항이 크면 전류가 천천히 흐르기 때문에 충전 시간이 길어지고, 커패시터의 용량이 크면 더 많은 전하를 저장할 수 있기 때문에 역시 충전 시간이 길어집니다.
이 과정을 쉽게 설명하자면, 저항은 전류가 커패시터로 들어가는 속도를 조절하고, 커패시터는 그 전류를 저장하는 그릇 역할을 하는 겁니다.
RC 회로 충전 시간은 단순히 이론적인 개념이 아니라, 실제로 많은 전자 기기에서 중요한 역할을 합니다.
예를 들어, 전자 시계의 타이머나 카메라의 플래시 충전 과정에서도 이 RC 회로 충전 시간이 중요한 역할을 합니다.
커패시터가 빠르게 충전되어 플래시가 켜질 준비가 될 때까지의 시간을 계산하는 데도 사용됩니다.
- 연관 참조 : RC 회로 방전 시간,전압 변화, 시간 상수, 예시1
- 연관 참조 : 미분기,회로 수식,RC 미분기 동작 원리,입력 파형에 따른 출력 파형, 예제1
- 연관 참조 : 적분기,RC 적분기 동작 원리, 예제1, 입력 신호에 따른 출력 변화
- 연관 참조 : RC 회로 상수 계산기, 장점 및 단점, 사용 방법
2. RC 회로에서의 충전 과정
2-1) 커패시터가 충전되는 원리
커패시터는 일종의 ‘전하를 저장하는 장치’입니다.
RC 회로에서 커패시터는 전하(Charge)를 모으기 시작하는데, 전원이 인가되면 전류가 흐르면서 커패시터에 전하가 쌓입니다.
처음에는 커패시터가 비어 있기 때문에 전류가 강하게 흐르고, 이때 전하가 빠르게 축적됩니다.
하지만 커패시터에 전하가 점차 쌓이면서 내부 전압이 증가하게 되면, 외부에서 들어오는 전류가 점점 저항을 받기 시작합니다.
결국 시간이 지나면서 더 이상 전하를 받을 수 없는 상태에 도달하게 되는데, 이때 커패시터가 ‘완전히 충전’되었다고 합니다.
종종 나오는 질문 중 하나가, “커패시터는 어떻게 충전되나요?”라는 질문입니다.
답변은 보통 “커패시터는 회로에서 전하를 모으는 부품이며, 전하가 쌓일수록 충전 속도가 느려집니다”라는 내용으로 돌아오게 됩니다.
바로 이 점이 RC 회로 충전 시간에서 중요한 부분입니다.
전하가 쌓일수록 충전이 느려지는 것은 커패시터 내부에 저장된 전하가 외부 전류와 반발하기 때문입니다.
이 현상을 통해 우리는 RC 회로가 충전되는 과정을 시각적으로 이해할 수 있습니다.
2-2) 충전 그래프와 시간에 따른 전압 변화
커패시터의 충전 과정은 단순한 직선 형태가 아닌, 곡선 형태로 그려집니다.
즉, 시간이 지남에 따라 커패시터의 전압이 증가하는데, 이 증가 속도가 처음에는 빠르다가 점점 느려집니다.
이 그래프를 그려보면, 충전 과정이 지수 함수(Exponential Function)에 따라 이루어짐을 알 수 있습니다.
흔히 말하는 “지수 증가”라는 개념인데, 커패시터의 충전 속도는 처음엔 빠르게, 시간이 지남에 따라 점차 느려지는 것입니다.
그래프에서 수직축은 전압, 수평축은 시간으로 표시되며, 충전이 진행될수록 전압이 천천히 증가하는 곡선이 나타납니다.
RC 회로 충전 시간의 핵심은 바로 이 지수적 변화에 있습니다. 이 과정에서 타임 컨스턴트(Time Constant, τ)가 매우 중요한 역할을 하는데, 타임 컨스턴트는 커패시터가 완전 충전될 때까지 걸리는 시간 중 약 63.2%에 도달하는 시간을 의미합니다.
예를 들어, RC 회로에서 저항이 커지거나 커패시터의 용량이 커지면 충전 시간이 길어집니다.
커패시터가 큰 물통이라면 더 많은 전하를 저장할 수 있으니 당연히 충전 시간이 더 걸리게 될겁니다.
저항이 크면 전류가 천천히 흐르기 때문에 충전 속도가 느려집니다.
반면 저항이 작으면 충전 시간이 빨라지게 됩니다.
이 과정을 상상해보시기 바랍니다.
물이 급하게 쏟아져 들어오다가 물통이 거의 찰수록 물이 천천히 들어오는 모습이 바로 이 그래프와 비슷합니다.
그래서 RC 회로에서의 충전 시간은 회로 설계에서 중요한 고려 사항이 됩니다.
타이머나 필터 회로처럼 시간에 민감한 전자 기기에서 이 RC 회로 충전 시간을 계산하여 적절한 값으로 조정할 수 있습니다.
3. RC 충전 시간 상수 (Time Constant)
RC 회로에서 충전 과정을 이해하는 핵심 개념 중 하나가 바로 타임 컨스턴트(Time Constant)입니다.
이 개념을 알면, 커패시터가 얼마나 빠르게 충전되는지, 즉 RC 회로 충전 시간이 얼마나 걸리는지를 정확하게 예측할 수 있습니다.
복잡해 보일 수 있지만, 타임 컨스턴트는 사실 꽤 단순한 물리적 의미를 가지고 있습니다.
3-1) 타임 컨스턴트의 정의
타임 컨스턴트는 보통 그리스 문자 τ (tau)로 표시되며, R(저항값)과 C(커패시턴스값)의 곱으로 정의됩니다.
즉, τ = R × C로 표현됩니다.
여기서 중요한 건 이 타임 컨스턴트가 무엇을 의미하느냐는 점입니다.
간단히 말해, 타임 컨스턴트는 커패시터가 완전 충전 상태의 약 63.2%까지 충전되는 데 걸리는 시간입니다.
왜 하필 63.2%일까요?
이는 RC 회로의 충전 과정이 지수 함수적(Exponential)으로 이루어지기 때문입니다.
시간이 지날수록 충전 속도는 점점 느려지지만, 타임 컨스턴트 τ 시간 안에는 상당한 양의 전하가 커패시터에 쌓이게 됩니다.
“RC 회로에서 타임 컨스턴트가 뭔가요?”라고 종종 질문하는데, 그에 대한 간단한 답변으로는 “타임 컨스턴트는 커패시터가 63.2%까지 충전되는 시간을 의미한다”라고 설명할 수 있습니다.
이 개념을 알고 있으면, RC 회로의 충전 속도를 직관적으로 파악할 수 있습니다.
3-2) RC 타임 컨스턴트가 충전 속도에 미치는 영향
RC 회로에서 충전 시간에 영향을 미치는 요소는 저항값 R과 커패시터의 C입니다.
두 값이 커질수록 타임 컨스턴트 τ는 커지며, 이는 커패시터가 더 천천히 충전된다는 뜻입니다.
반대로, 저항이나 커패시턴스 값이 작아지면 타임 컨스턴트는 짧아져 충전이 빠르게 이루어집니다.
이를 물통에 물을 채우는 상황에 비유해 보면, 저항은 물이 흐르는 배관의 굵기, 커패시턴스는 물통의 크기와 같습니다.
물통이 크거나 배관이 좁으면 물이 채워지는 데 시간이 오래 걸릴 수 밖에 없습니다.
타임 컨스턴트가 크다는 것은 RC 회로 충전 시간이 길어진다는 것을 의미합니다.
반대로 타임 컨스턴트가 작으면 충전이 빠르게 이루어집니다.
타임 컨스턴트가 1초라면, 1초가 지난 후 커패시터는 최대 전압의 63.2%까지 충전됩니다.
타임 컨스턴트가 5초라면, 5초 동안 커패시터는 더 천천히 충전될 것입니다.
충전 속도를 이해하려면 지수 함수 그래프를 살펴보는 것이 좋습니다.
충전이 시작된 후, 처음에는 매우 빠르게 전하가 쌓이지만 시간이 지남에 따라 충전 속도가 급격히 느려집니다.
약 5τ(타임 컨스턴트의 5배) 시간이 지나면 커패시터는 거의 완전히(99% 이상) 충전됩니다.
따라서, RC 회로를 설계할 때 타임 컨스턴트는 필수적으로 고려되어야 하는 요소입니다.
예를 들어, 타이머 회로를 설계할 때, 타임 컨스턴트가 너무 짧으면 시간이 충분하지 않고, 너무 길면 반응 속도가 느려질 수 있습니다.
결국 RC 회로 충전 시간은 타임 컨스턴트에 의해 결정됩니다.
4. RC 회로에서의 전압 및 전류 변화
RC 회로 충전 시간을 이해하기 위해서는 커패시터가 충전되는 동안 전압과 전류가 어떻게 변하는지를 살펴보는 것이 매우 중요합니다.
커패시터는 시간에 따라 전하를 저장하면서 그 상태에 따라 전압과 전류가 달라집니다.
이러한 변화는 지수 함수적인 패턴을 따르며, 이를 통해 충전 과정을 보다 명확하게 이해할 수 있습니다.
4-1) 충전 중 전압과 전류의 변화 분석
RC 회로에서 스위치를 닫고 충전이 시작되면, 처음에 커패시터의 전압은 0V입니다.
이때 커패시터는 아직 전하를 저장하지 않았기 때문에 회로의 저항은 전류의 흐름을 거의 막지 못하고, 최대 전류가 흐르게 됩니다.
이 초기 전류는 저항값과 전원 전압에 의해 결정되며, I = Vs / R의 법칙을 따릅니다.
쉽게 말해, 스위치를 처음 닫았을 때는 저항만큼의 제약을 받지만, 시간이 지나면서 커패시터가 충전되면 점차 전류가 줄어듭니다.
이 전류의 감소는 커패시터에 저장되는 전하가 늘어나면서 발생합니다.
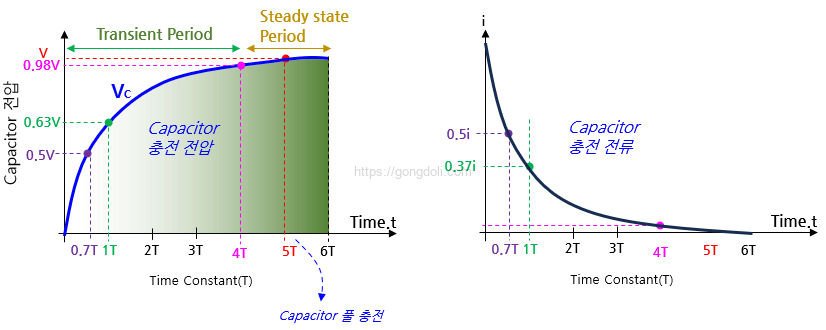
시간이 지남에 따라 커패시터가 충전되면, 커패시터 양단의 전압이 상승하고, 결국에는 전원 전압과 동일한 값에 도달하게 됩니다.
즉, 시간이 지남에 따라 전압은 증가하고, 반대로 전류는 감소하는 경향을 보입니다.
이를 좀 더 구체적으로 살펴보면, RC 회로 충전 시간 동안 전압은 지수 함수적으로 증가하며, 전류는 지수 함수적으로 감소합니다.
4-2) 수식을 통한 간단한 설명
이제 이를 수식을 통해 간단히 설명해 보겠습니다.
RC 회로에서 충전 중의 전압 변화는 다음과 같은 지수 함수로 표현됩니다.

- 수식에서
Vc(t)는 시간 t에서의 커패시터 전압
Vs는 전원 전압
R은 저항 값, C는 커패시턴스 값
t는 시간, 그리고 RC는 타임 컨스턴트(τ)
이 식을 보면, 시간이 지날수록 e(-t/RC) 항이 0에 가까워지기 때문에, Vc(t)는 점차 Vs에 가까워진다는 것을 알 수 있습니다.
즉, 커패시터는 시간이 지남에 따라 전원 전압에 수렴하게 됩니다.
반면, 전류는 충전이 진행됨에 따라 감소하며, 이 역시 지수 함수로 표현됩니다.

- 여기서
I(t)는 시간 t에서의 회로 전류
Vs / R은 초기 전류 값
이 수식에 따르면, 시간이 지날수록 e(-t/RC) 항이 0에 가까워지므로, 전류는 점점 줄어들어 충전이 끝나면 전류가 0이 됩니다.
즉, RC 회로에서 시간이 지남에 따라 커패시터의 전압은 증가하고, 전류는 감소하는 패턴을 보이게 됩니다.
이 두 가지 수식은 RC 회로 충전 시간에 대한 중요한 정보를 제공해 줍니다.
커패시터가 완전히 충전되기까지의 시간과 충전 중 전압, 전류의 변화를 예측하는 데 필수적입니다.
회로를 설계할 때 이 수식을 통해 타이밍이나 충전 속도를 계산할 수 있습니다.

Wonderful web site. A lot of useful information here. I’m sending it to several friends ans also sharing in delicious. And naturally, thanks for your effort!
Thank you for your kind words! We’re thrilled that you find our website useful and appreciate you sharing it with your friends. Your support means a lot to us, and we’ll continue to work hard to provide valuable content
Thanks for the sensible critique. Me & my neighbor were just preparing to do some research on this. We got a grab a book from our area library but I think I learned more from this post. I am very glad to see such excellent information being shared freely out there.
You’re very welcome! I’m delighted to hear that the information was helpful to you and your neighbor.
I like what you guys are up too. Such intelligent work and reporting! Keep up the superb works guys I have incorporated you guys to my blogroll. I think it will improve the value of my website :).
hat’s amazing! It’s really encouraging to know that you appreciate the work. Adding it to your blogroll is a great compliment
you have a great blog here! would you like to make some invite posts on my blog?
Thank you so much for the kind invitation.
I truly appreciate it! Unfortunately, I’m currently tied up with work and won’t be able to write any posts at the moment.
Excellent blog here! Also your web site loads up fast! What host are you using? Can I get your affiliate link to your host? I wish my website loaded up as fast as yours lol
Thanks so much for your thoughtful message!
I’m really glad you’re inspired to start your own blog.
This site is built on WordPress and is currently hosted with a Korean hosting provider.
You should take part in a contest for one of the best blogs on the web. I will recommend this site!
Wow, thank you so much for the amazing compliment!
I’m truly honored that you think this site is worth recommending.
You have observed very interesting details! ps decent site. “The empires of the future are the empires of the mind.” by Sir Winston Leonard Spenser Churchill.
Appreciate that—and what a powerful quote to reflect on!
excellent points altogether, you just gained a emblem new reader. What might you suggest about your submit that you made a few days ago? Any sure?
Thank you—I appreciate your feedback, and I’ll keep sharing more posts soon.
I’m extremely impressed with your writing skills and also with the layout on your blog. Is this a paid theme or did you modify it yourself? Either way keep up the excellent quality writing, it is rare to see a nice blog like this one nowadays..
Thank you! I appreciate your kind words and I’m glad you enjoy both the writing and layout.
I am glad for commenting to let you know what a wonderful encounter my cousin’s girl developed reading your webblog. She discovered a good number of pieces, with the inclusion of what it’s like to possess an incredible giving mindset to make the mediocre ones with ease learn about chosen advanced subject areas. You undoubtedly exceeded her desires. Many thanks for presenting these precious, safe, informative and in addition cool tips about that topic to Janet.
Thank you! I’m glad the blog was helpful and that Janet enjoyed the tips.
Wow! Thank you! I continuously needed to write on my blog something like that. Can I implement a part of your post to my blog?
I appreciate your interest. You’re welcome to reference or quote a short part of the post on your blog, as long as you provide proper credit and a link back to the original source.
Pretty! This was a really wonderful post. Thank you for your provided information.
Thank you so much for your kind words.